小型化地波雷达海杂波散射系数仿真及SVD抑制方法研究＊

王春雨 卢庆广 左 雷 马红星

（1.海军工程大学电子工程学院海洋电磁环境研究所 武汉 430033）（2.海军驻合肥地区军事代表室 合肥 230000）

1 引言

海表面对雷达发射信号的后向散射回波被称为海杂波或海表面回波［1］。海杂波是目标检测背景中的主要杂波，落入海杂波的目标常常被掩埋，甚至存在盲区，通过海杂波的研究，主要目的是在雷达回波信号中抑制海杂波，从而提取出目标信息。

2 海杂波机理

海面散射的高频电磁波谱主要由两部分组成：一种是由满足布拉格（Bragg）衍射条件的海浪波长所形成的对称谐振谱峰，又称一阶回波。当目标处于一阶峰附近时，其强度比目标高很多，目标信号很容易被掩盖，造成速度盲区。另一种是比一阶回波谱低20～40dB的二阶回波，又称作高阶海杂波，它是由小海浪引起的散射回波以及海面波经多次反射后回到雷达的回波谱［2］。

1）高频地波雷达回波功率模型

文献［3］推导出单基地收发共址情况下海杂波功率谱密度为

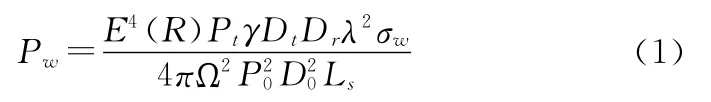
式中σw＝RtΔRΔθσ0（f0）为海浪的有效散射截面积，其中，Rt为雷达的作用距离，ΔR为距离分辨率，Δθ为角分辨率，σ0（f）为单位面积、单位频率上的海浪散射截面即海浪散射系数。因此，对海杂波的认识研究，应首先对海浪散射系数的研究。

（1）一阶海杂波雷达散射系数

由于天线阵的小型化，高频地波雷达一般为宽波束雷达，考虑波束照射海区为单一海流，即一阶峰的展宽主要是由于径向海流在回波各个方位的投影值不同所造成的，宽波束雷达的一阶海浪散射系数为［4］

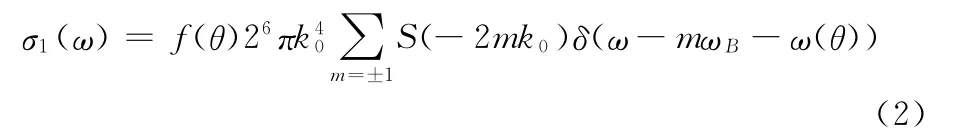
（2）二阶海杂波雷达散射系数

波束照射海域为深水区且不存在海流的情况下，Bar－rick推导出雷达二阶海浪散射系数为［5］

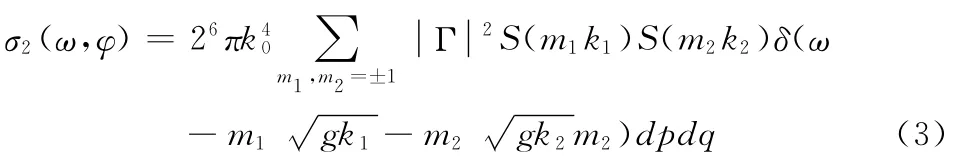
2）海浪散射系数仿真分析

根据前面建立的海浪散射系数模型，采用有向浪高谱采用 Pierson－Moscowitz谱［6］：

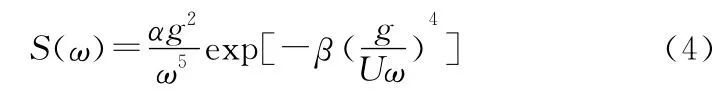
其中，常数α＝8.10×10－3，β＝0.74，g为重力加速度，U 为海面上7.5m处的风速，利用数值积分方法并进行数值平滑后得到不同雷达工作频率f0、海面风速V、海面风向O下海浪散射系数如图1～图3所示。

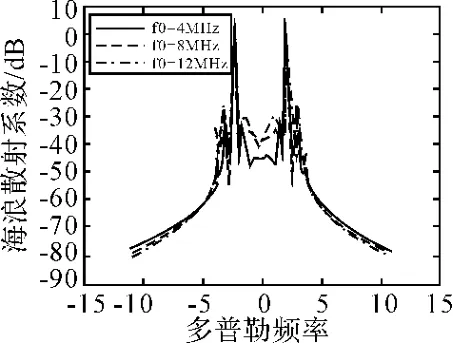
图1 风速10m／s，风向0°下不同雷达工作频率对海浪散射系数影响

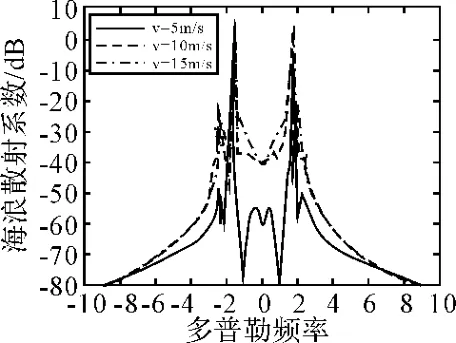
2 工作频率为8MHz，风向为0°下不同风速对海浪散射系数影响

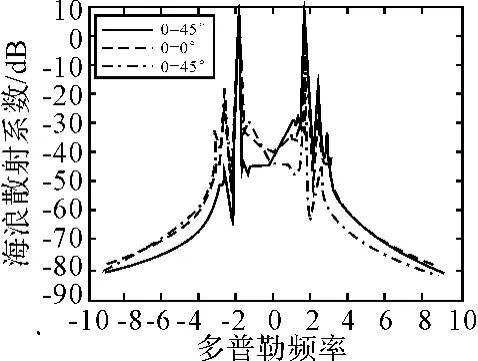
图3 风速10m／s，工作频率为8MHz下不同风向对海浪散射系数影响

可得一阶、二阶海杂波的谱特征与频率及海洋环境之间具有如下关系：

风速恒定情况下，一、二阶谱的幅度随载频的增加而增加，载频越高情况下激励的海杂波的波长越小，较小的风就能引起谐振波产生，所以载频越高海杂波就越强；一、二阶幅度差与海态（波高的均方根值）关系较大，两个一阶Bragg峰的幅度差与Bragg谐振波（表面风向）有关，且风向严重影响了二阶谱的能量分布；二阶散射结果包括连续且部分相关的强离散成分，当风速增加时二阶海杂波得到充分发展，其能量大幅度增加，给定Doppler位置的二阶连续谱的水平将随雷达频率和海态的增加而增高，且在频率上展宽。

3 SVD海杂波抑制

通过对海杂波反射系数仿真可以看到，海杂波是海上目标检测的最大难题。近年来，奇异值分解（SVD，singular value decomposition）在信号处理处理中的应用越来越广，主要应用在信号的最小平方估计、ARMA模型求解、噪声去除等方面［8］。采用时间序列的Hankel矩阵的奇异值分解（SVD）方法可以从雷达回波信号中选择去除杂波信号分量，从而有选择性的抑制海杂波。

1）奇异值分解理论

设A是m×n矩阵，秩为r，则存在酉矩阵P和Q，使得

其中，P和Q 大小分别为m×m，n×n，S＝diag（σ1，σ2，σ3，…，σr），且σ1≥σ2≥σ3≥…≥σr＞0，σi（i＝1，2，…，r）称为A的奇异值，P和Q的列向量pi，qi分别是A的左、右奇异向量。

设回波信号由几个时变频率信号和噪声叠加，即x（n）＝s（n）＋u（n），其中s（n）对应于信号，u（n）对应于不确定杂波及噪声。已知信号x（n）序列长度为N（n＝1，2，…，N），构造矩阵

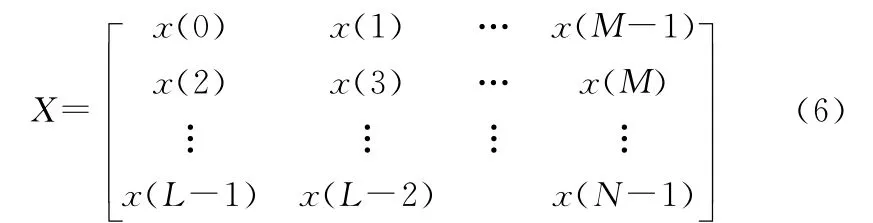
由时间序列构建的Hankel矩阵A可以看作是由信号、杂波干扰和噪声共同组成的矩阵，那么σ1，σ2，σ3，…，σr反映了信号、杂波干扰和噪声的能量集中情况。由于一阶海杂波集中在正负Bragg峰附近，且远高于目标及其他杂波强度，不妨将其视为频率集中在正负Bragg峰的两个大目标回波那。前i个较大的奇异值将依次主要反应大的信号能量，较小的奇异值则反映出噪声，中间部分则主要对应于二阶海杂波、慢小目标及其他杂波，将一阶海杂波和部分反映噪声的奇异值置为零，重建后能较好地消除海杂波及去除噪声。

2）仿真分析

将某型地波雷达2012年4月27日在东海某试验场0958时刻记录数据，通过预处理并进行一次FFT后在距离雷达90km处加入速度为1.9m／s，信杂噪比为12dB的仿真目标后得到多普勒图如图2所示。

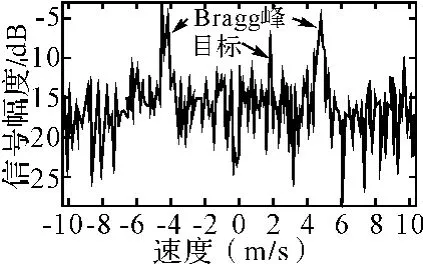
图4 含仿真目标回波的多普勒图

从图4中可以看出一阶Bragg峰在回波中所占能量最高，严重影响了目标的检测，必须对其进行抑制。采用SVD方法，选取合适的M值，构造Hankel矩阵，通过SVD分解后，分别将主要对应一阶海杂波能量的两特征值置零和将除主要对应目标的特征值保留外，其余特征值均置零后信号重建所得多普勒图如图5和图6所示。

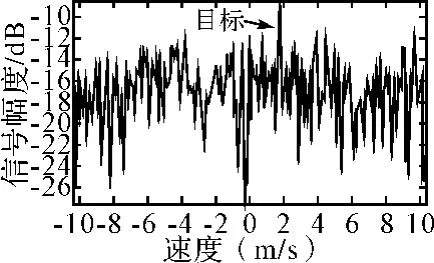
图5 SVD抑制一阶海杂波后的多普勒图

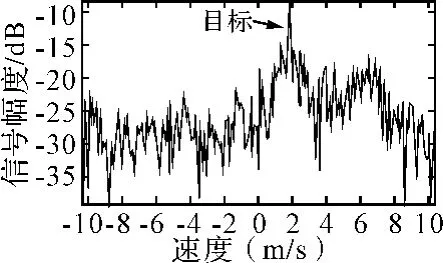
图6 SVD抑制海杂波后的多普勒图

从图5明显可以看出，一阶海杂波得到了很好的抑制，几乎与杂噪基底持平，而目标能量基本保持不变。从图6可以看出，二阶海杂波也相应削弱了，信号的信杂比得到明显增强。

4 结语

通过仿真分析，对海杂波机理及其影响因素进行了深入探讨，仿真分析了风速、风向、雷达工作频率对海浪散射系数影响，为海杂波的抑制提供了理论基础。采用实测数据加入仿真目标的方法对SVD海杂波抑制方法效果进行了仿真研究，表明了基于奇异值分解的SVD海杂波抑制方法对于海杂波及噪声具有较好的抑制作用，对海杂波的抑制提供了很好的参考价值。

［1］M.I.Skolnik.Radar Handbook，3rdEdition［M］.Artech House，2008：15.1.

［2］曲翠萍，李秀峰.高频地波超视距雷达的特点和用途［J］.雷达与对抗，2007（2）：1－3.

［3］董英凝，张宁，许荣庆.高频地波雷达工作环境对系统性能影响的分析［J］.电波科学学报，2007，22（2）：325－310.

［4］雷志勇，文必洋，程丰.基于自适应对消法检测一阶Bragg峰内目标的研究［J］.电波科学学报，2006，21（3）：365－370.

［5］Barrick D.First－order theory and analysis of MF／HF／VHF scatter from the sea［J］.IEEE Trans.on Antennas and Propagation，1972，20（1）：2－10.

［6］WEN Sheng－chang，YU Zhou－wen.Ocean Wave Theory and Calculation Principles［M］.Beijing：Science Publications，1984（Ch）.

［7］赵建军，肖雄波，杨利斌.基于AR模型和ZMNL变换的K分布海杂波仿真方法［J］.计算机与数字工程，2011（8）.

［8］胡广书.数字信号处理［M］.北京：清华大学出版社，2003：441－445.