基于半确定性面元模型的海面散射系数仿真
冯 明,安 锐,张润俊
(电磁散射重点实验室,上海 200438)
0 引言
传统海面电磁散射模型通过求集平均的方法来统计得到不同海况输入参数下的海面散射系数,不需要具体的海面几何样本。常用的方法包括基尔霍夫近似(Kirchhoff Approximation,KA)法[1]、微扰法[2]、双尺度法[3]等。然而,仅用统计模型得到的海面散射系数来获得海面回波是无法满足海面合成孔径雷达(Synthetic Aperture Radar,SAR)图像解译等应用需求的。统计模型无法给出各散射单元的散射贡献,很难分析海表面的尾迹、碎浪、油污等分布特征,应用范围受到较大限制。本文从确定性的海面几何样本出发,提出了一种基于面元的海面散射仿真模型。在该仿真模型中,海面样本的基尔霍夫散射和布拉格(Bragg)漫散射均基于面元进行计算,既可获得不同面元的散射特征,又可获得海面样本总的散射特征。基于面元的海面散射模型适合海面SAR图像解译和海洋遥感等应用,扩展了海面电磁散射的应用范围。
1 海面面元散射系数模型
基于Fuks微扰解推导了倾斜面元上粗糙表面的散射系数,用海谱中的毛细波谱部分来描述微粗糙表面。建立了海面面元Bragg散射计算模型,并在垂直入射区进行KA修正,建立了修正的面元散射计算模型。
1.1 Fuks微扰解的基本公式
单位入射波照射高低起伏均值为0的微粗糙表面,Fuks微扰解的基本公式给出了散射幅度的表达式,利用微粗糙表面的空间功率谱推导了微粗糙表面的雷达散射系数。
如图1所示,ki,vi,hi分别为入射波的入射方向、电场方向、磁场方向单位矢量,ks,vs,hs分别为散射波的散射方向、电场方向、磁场方向单位矢量,θi,θs,ϕs分别为入射俯仰角、散射俯仰角和散射方位角,微粗糙表面的高低起伏ζ(r)均值为0,其分布具有空间齐性,r为表面上点的位置矢量。假设上半空间(z>ζ(r))为真空介质,即相对介电常数为1,下半空间 (z≤ζ(r))的相对介电常数为ε。根据Fuks所给出的一阶微扰解公式,考虑单位平面波Ei沿平面xoz入射,则散射幅度可表示为[4]
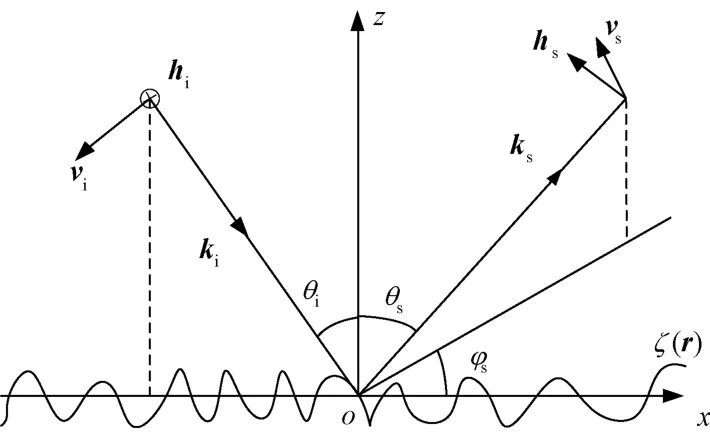
图1 微粗糙表面散射示意图

式中:k为电磁波波数大小;Fpq为极化因子,下标p=h,v表示散射波矢量的极化方式(h表示水平极化,v表示垂直极化),q=h,v表示入射波矢量的极化方式;q=k(ks-ki)。极化因子可以表示为

式中:Rv和Rh分别为两种极化下的菲涅尔反射系数。
假设接收点到坐标中心的距离为R0,则单位面积的散射场可表示为


式中:<·>表示求集平均;r'为表面上点的位置矢量;Sζ(ql)是微粗糙面的空间功率谱;ql为q在均值面(z=0)上的投影矢量。
1.2 倾斜粗糙面元电磁散射建模
根据Fuks微扰解可以推导任意倾斜面元散射系数的微扰计算公式。

图2 全局直角坐标系与本地坐标系示意图
如图2所示,oxgygzg为全局直角坐标系,在微粗糙面上建立本地坐标系
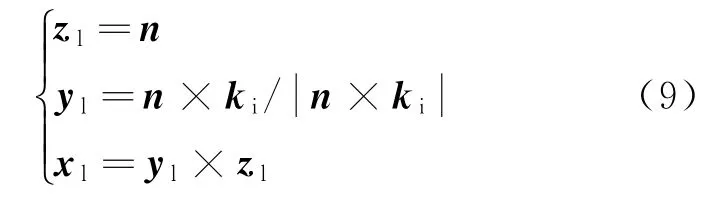
式中:n为小面元的法向矢量。定义入射和散射方向在两种坐标系下对应的全局角与本地角分别为 (θi,θs,ϕi,ϕs)和,所对应的单位极化矢量分别用(Hi,Vi,Hs,Vs)和 (hi,vi,hs,vs)表示,根据矢量分解可以得到[5]
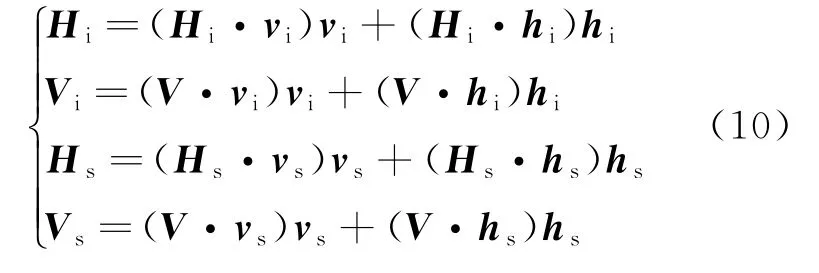

那么,任意倾斜粗糙面元的散射系数可以表示为

1.3 半确定性面元散射仿真模型的建立
至此可以计算任意倾斜粗糙面元的散射贡献。若忽略各个面元之间的相互作用以及多次散射,将所有的面元散射叠加起来,即为总的散射贡献。这样即可将海面总回波与具体时刻海面样本对应起来。这种对确定海面几何特征电磁散射建模的思想称为半确定(半统计)。微粗糙海面的空间功率谱可采用单边谱的高频部分,则面元的散射系数可表示为
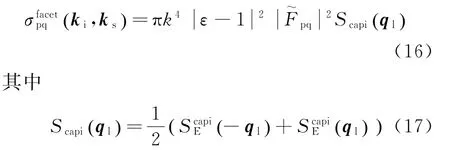
式中:Scapi(ql)为对雷达有贡献的Bragg毛细波成分。这里用毛细波谱来描述面元的小尺度结构,用截断波数将单边谱划分为大尺度重力波谱和小尺度毛细波谱两部分,表达式为

式中:SE(k)为二维海谱;kcut为截断波数;k为海浪波数方向矢量。假设二维海面模拟样本在x和y方向的长度分别为Lx和Ly,面积为A,等间隔离散点数为M和N,相邻两点间的距离分别为Δx和Δy,将所有面元的散射系数叠加起来,即可得到总的散射系数
总散射系数在近垂直区域的预估值对截断波数的依赖度较高。引入基尔霍夫近似模型,修正倾斜调制的微扰系数[6],得到修正后的总的散射系数
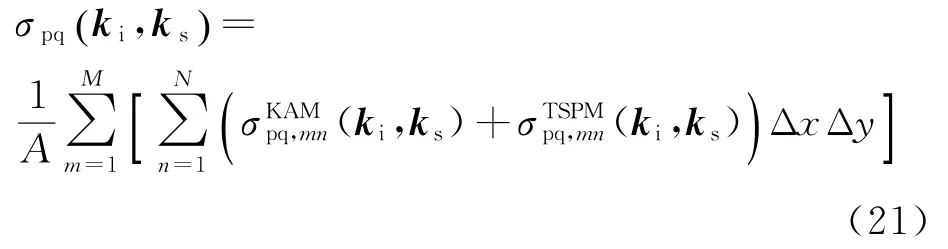
2 海面散射系数仿真与验证
为了与造波池模拟的海谱相对应,使用Pierson-Moscowitz(PM)谱生成海面几何模型。仿真的频率为X波段和Ku波段,极化方式为vv、hh极化,生成海面模型的尺寸为100 m×60 m,空间离散间隔Δx=Δy=0.5 m。本文主要仿真海面后向散射系数。
仿真海况为1级,入射频率为10 GHz。将仿真结果与造波池测试数据进行对比,结果如图3所示。vv极化的后向散射系数均方根误差为2.2 d B,hh极化的均方根误差为2.6 d B。

图3 X波段1级海情后向散射系数仿真与测试对比
仿真海况为3级,入射频率为16 GHz,将仿真结果与造波池测试数据进行对比,结果如图4所示。vv极化的均方根误差为2.5 dB,hh极化的均方根误差为3.0 d B。
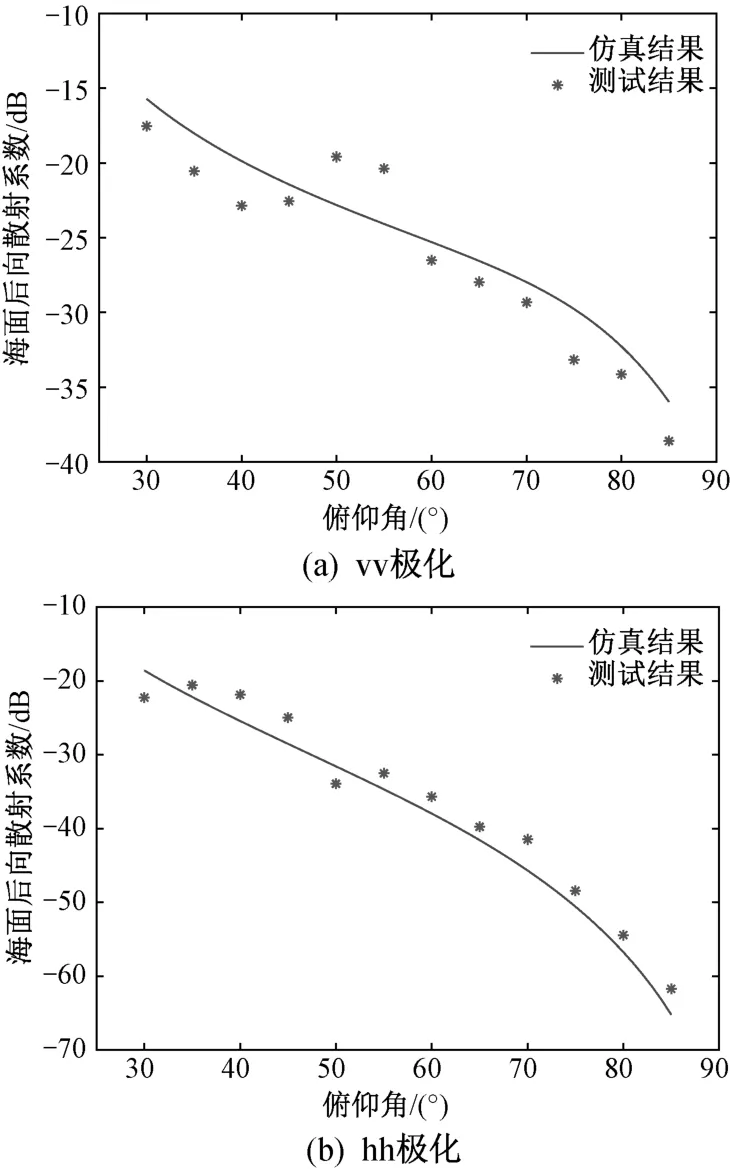
图4 Ku波段3级海情后向散射系数仿真与测试对比
图3和图4的仿真与测试结果之间的后向散射系数的均方根误差在3 dB以内,在建模精度与测试误差允许范围内,仿真结果具有较高的可信度。
为了验证本文提出的半确定性面元模型计算海面双站散射系数的准确性,仿真了双站海面散射系数,并与AWADA等[7]给出的小斜率近似(Small-Slope Approximation,SSA)结果进行对比,如图5所示。仿真时海面样本采用线性滤波法生成,海况3级,风速5 m/s,逆风方向。取离散间隔Δx=Δy=0.5 m,离散点数512×512。雷达频率为14 GHz,入射俯仰角和方位角分别为50°、0°,散射方位角为0°。

图5 双站散射系数随俯仰角的变化
由图5可知,在散射俯仰角为50°时,即镜像点左右,产生峰值,且本文方法的仿真曲线与SSA仿真曲线基本吻合,验证了本文提出的半确定性面元模型在海面双站散射系数计算中的准确性。
3 结论
本文研究了海面散射系数仿真建模方法,建立了基于半确定性面元模型的海面电磁散射系数仿真模型,对典型海面的电磁散射系数进行了仿真,并与造波池测试数据和文献数据进行了对比,仿真结果验证了模型的正确性。

