一种基于STFT的脉内调制识别方法优化与分析

王 璐，张学辉

(北京华航无线电测量研究所，北京 100010)

0 引言

现代电子对抗的电磁环境日益复杂，信号分布愈加密集，辐射源数量也持续增长，多个信号同时到达的情况也随之出现。为了满足抗干扰、反侦察等需要，现代雷达会对发射信号进行复杂的脉内调制，并使用可变参数的发射信号，这对雷达辐射源信号的分选识别带来极大的挑战[1-2]。雷达信号脉内分选和识别是电子侦察系统进行目标识别的重要手段[3]。自20世纪80年代末期开展雷达辐射源信号脉内特征提取的研究以来[4]，该领域的研究就从未停止。文献[2]提出了一种基于线性正则变换与短时傅里叶变换联合的时频分析方法，避免交叉项问题的同时又实现了线性调频信号的干扰抑制和多分量时频信号分离。文献[5]提出的基于信号能量聚焦效率检验的识别算法，解决了低信噪比条件下信号调制的盲识别问题。与雷达信号处理技术结合，文献[6]采用模糊函数完成了辐射源信号的脉内特征识别。文献[7]研究了一种神经网络与脉内分析结合的信号调制识别方法，并验证了算法的正确性。

针对线性调频(Linear Frequency Modulation，LFM)、非线性调频(Nonlinear Frequency Modulation，NLFM)和频率步进等信号的精细分类，传统方法以信号瞬时频率曲线的线性度作为特征识别参数，但传统方法存在对三次曲线调制NLFM信号识别概率偏低的问题。为了解决这一问题，本文提出一种新的特征识别参数，对识别流程进行调整，并通过仿真验证改进算法对提高频率调制信号精细分类识别概率的有效性。

1 典型辐射源信号脉内调制识别算法

1.1 短时傅里叶变换算法

短时傅里叶变换的基本原理是在待分析的辐射源信号上加一个随时间移动的窗，使用该窗函数对源信号进行截取。假设在窗函数截取范围内信号是平稳的，对截取后的信号进行傅里叶变换，即可得到源信号在不同时刻的频率域信息。

连续信号r(t)时域短时傅里叶变换的数学表达式为

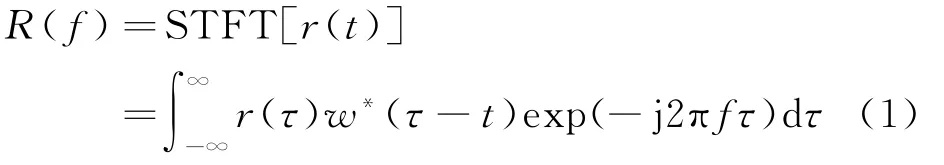
式中:w(t)为窗函数；“*”表示复共轭；f为信号频率。w(t)宽度决定了STFT的时域定位性能与频率分辨率，是利用STFT实现辐射源信号脉内分析的重要参数之一。

STFT可以反映信号的局部特征，并且算法计算量相对较小，在信号分析上具有一定的优势，是一种十分有效的时频分析法。然而，STFT本身也存在缺陷:由于不确定性原理的限制，STFT的时间分辨率和频率分辨率始终是一对矛盾，即不能在加长时间窗改善频率分辨率的同时提高变换的时间分辨率。此外，时间窗的长度越长，假设的信号平稳性就越不能保证。

1.2 Wigner-Ville变换

Wigner-Ville分布(Wigner-Ville Distribution，WVD)是由Wigner提出的一种具有双线性形式的时频分布函数，它在一定程度上解决了STFT存在的问题。它具有明确的物理意义，能够反映信号能量随时间和频率变化的分布。

对于连续信号r(t)，其 WVD时域变换公式为

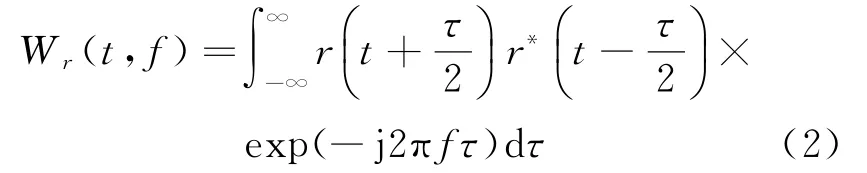
需要说明的是，如将信号离散化并对其进行加窗处理，时间窗的存在必然会导致信号频率分辨率的下降。但是这种处理会降低WVD变换的运算量，使得信号处理的实时性有所提高，适合实际工程应用。

1.3 相位差分算法

基于相位差分的脉内调制识别算法以最小二乘多项式拟合和直方图统计为主，非线性拟合和峰值检测为辅，通过最小二乘拟合、自适应阶数直方图统计和谱峰搜索等处理，完成输入源信号的分选识别。实际处理过程中，为了提高算法对低信噪比情况的适应能力，通常采用N阶相位差分运算，其计算公式为

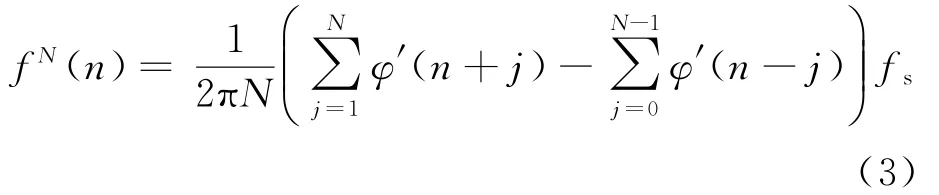
式中:φ'(n)表示信号n时刻的瞬时相位；fs为采样频率。

N阶相位差分运算实际上是一种平滑过程，可以有效地提高算法在低信噪比情况下的处理能力。但它不能有效地压制旁瓣，为此本次实验加入了有限冲激响应(Finite Impulse Response，FIR)滤波器。当信号经过低通滤波后，为了得到正确的瞬时频率值，必须进行拟合修正。

对相位编码信号的精细分类以及与频率编码信号的区分，需要利用自适应阶数统计直方图。当直方图宽度B确定后，直方图阶数Mstep的计算公式为

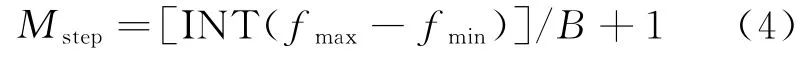
式中:INT(·)表示趋近0取整；fmax和fmin分别为相位编码信号瞬时频率的最大和最小值。确定阶数后，即可完成频点统计。直接计算得出的统计信息并不能方便地提取频点个数，需要将结果进行低通滤波。

基于相位差分的脉内调制识别算法将固定门限与自适应门限相结合，可以精确描述信号的宏观个体差异。由于使用了自适应阶数直方图统计等方法，可以利用回波信号的全部信息，提高了算法在低信噪比情况下的适应能力。

2 基于STFT的脉内调制识别算法改进

对LFM、NLFM和频率步进等三种频率调制信号进行脉内调制识别，传统方法是对调制信号进行STFT，提取辐射源信号瞬时频率曲线的线性度L和信号频谱包络中心频率点与其相邻频点间对应包络值的差δcenter，即

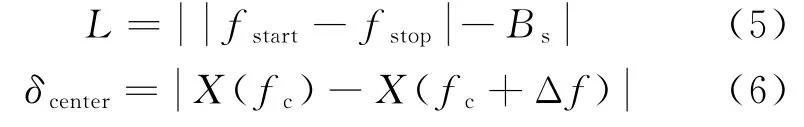
式中:fstart与fstop分别表示瞬时频率的起始和截止频率；Bs为信号带宽，是用于辐射源信号脉内调制识别的特征参数之一；X(·)表示信号频谱包络；fc为信号频谱包络中心频率；Δf为相邻频点间隔。基于STFT算法的三种频率调制信号的识别流程如图1所示。

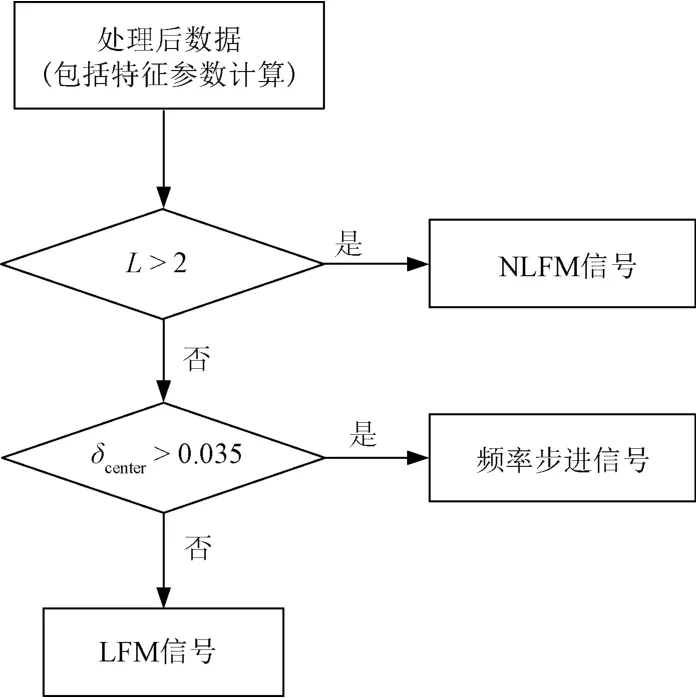
图1 基于STFT算法的频率调制信号脉内调制识别流程

信噪比10 d B条件下，三种频率调制辐射源信号经过STFT变换后的时频分布情况如图2所示。STFT算法对三种频率调制信号的识别概率偏低，尤其对NLFM信号。

从三种信号的时频分布图可以直观地看出，三者的时频特性极为相似。当对信号进行非线性频率调制时，若采用三次曲线调制且调制系数不大，则NLFM信号与LFM信号在瞬时频率的线性度指标方面过于接近甚至相同，二者识别容易混淆。同样频率步进信号与LFM信号的调制识别也会遇到困难。图2所示的信号时频分布结果是在信噪比10 dB条件下获得的，若信噪比降低，则传统方法对不同调制类型辐射源信号的识别概率必然降低。

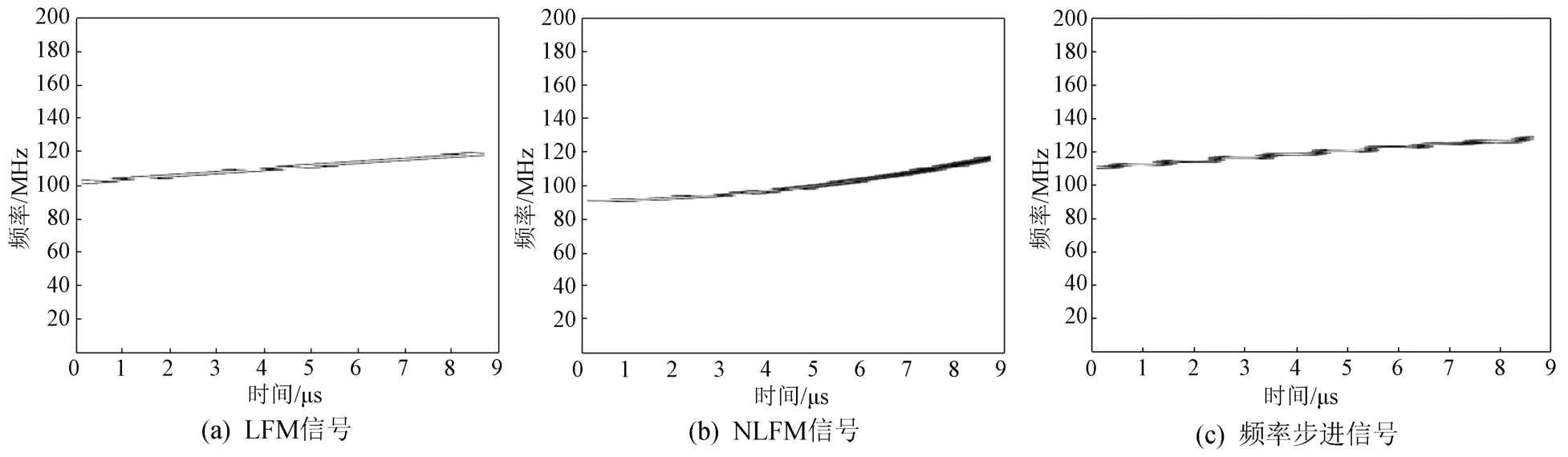
图2 辐射源信号STFT变换结果

为了解决上述问题，对三种信号的特征进行进一步分析。在频谱包络区域，三者有非常明显的区别，图3(a)～图3(c)分别为10 dB与-2 dB条件下，LFM信号、NLFM信号与频率步进信号的频谱包络。可以发现，LFM信号频谱包络的顶部区域比较平坦，NLFM信号频谱包络的顶部区域呈单调下降趋势，而频率步进信号频谱包络的顶部区域抖动极其明显。同时，在-2 dB低信噪比条件下，辐射源频谱包络虽有畸变，但是三者之间的差异依旧明显。由此可见，利用信号频谱包络提取特征参数的方法可行。

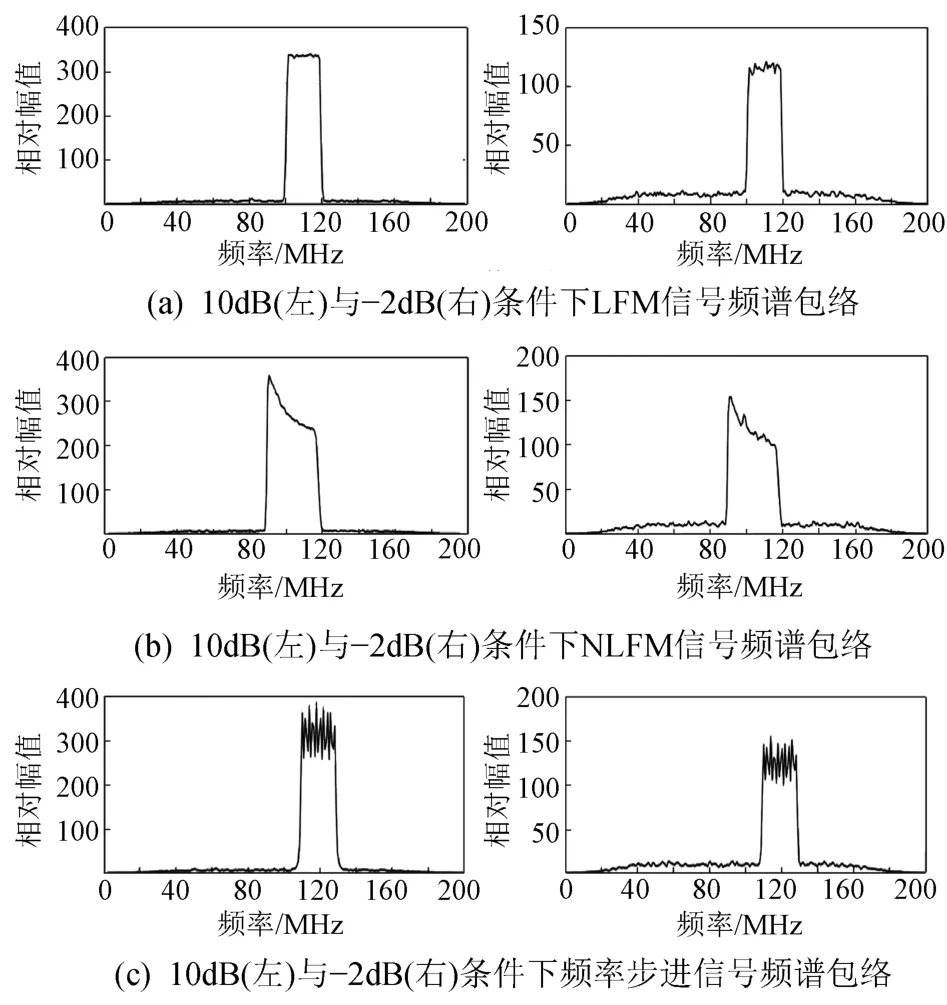
图3 辐射源信号频谱包络

为表征不同调制信号频谱包络间的区别，结合多次实验调整，除用δcenter表征包络顶部区域的抖动程度外，新增一个特征参数δmax-min。δmax-min表示频谱上大于门限的最小频率fmin与大于门限的最大频率fmax对应包络值之间的差，表达式为

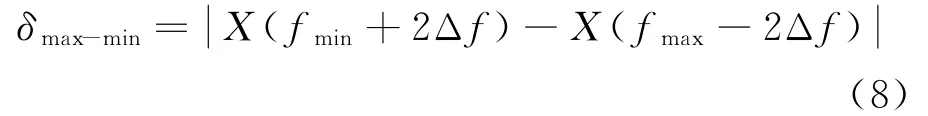
改进前后的信号识别流程如图4所示。

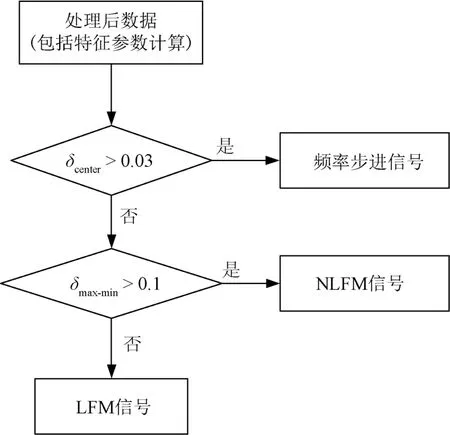
图4 改进后STFT算法频率调制信号脉内调制识别流程

利用信号带宽Bs、信号有效带宽Bv等脉内调制识别的特征参数，将算法适用范围拓展到恒频、LFM、NLFM、频率步进、二进制相移键控(BPSK)、正交相移键控(QPSK)、频移键控(FSK)等七种信号的脉内调制识别，流程如图5所示。其中所有参数判别门限均为经验值，应根据具体使用范围及仿真情况进行调整。

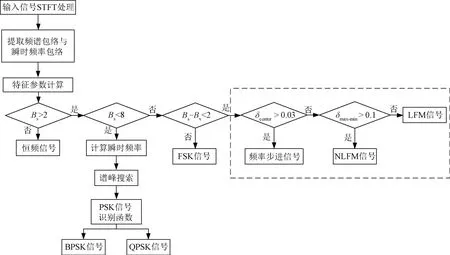
图5 辐射源信号脉内调制识别流程图

3 仿真验证

3.1 识别概率仿真

以LFM、NLFM、频率步进三种频率调制信号为例，在信噪比为-5，2，10 d B条件下，分别进行100次蒙特卡罗实验。对改进前后STFT算法的识别率进行仿真对比，结果见表1。

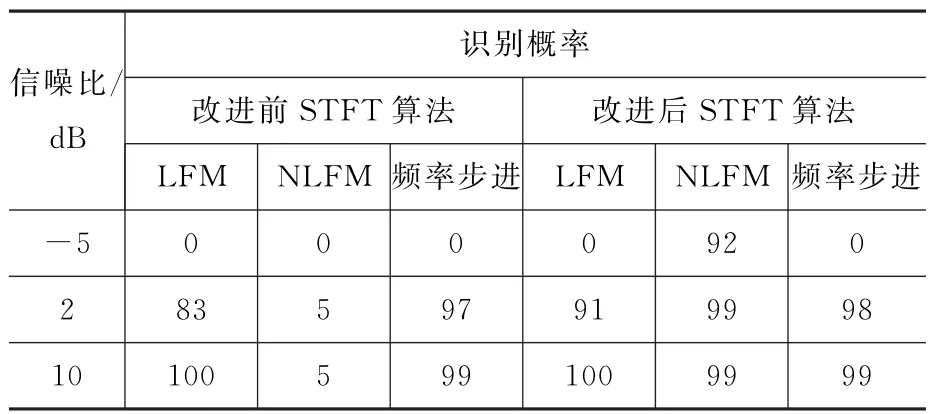
表1 改进前后STFT算法蒙特卡罗实验识别概率统计 %

由表1可知，算法改进后，对NLFM信号的识别概率大幅提高，尤其在-5 d B低信噪比条件下识别概率提升最为显著。对LFM信号与频率步进信号的识别概率在低信噪比条件下也有小幅提高。当信噪比达到2 d B时，改进后算法对三种频率调制信号的识别概率均达到90%以上，实验结果表明算法改进有效。

3.2 算法抗噪性验证

设输入源信号为某单一类型辐射源，共七种类型，采样频率3.2 GHz，信道化部分共32个信道，信噪比范围(-5～+15)dB。每隔0.5 d B选定信噪比进行100次蒙特卡罗实验。

(1)点频信号

输入点频信号，信道化处理后进行脉内调制类型识别与脉内参数估计，蒙特卡罗仿真实验结果见图6。当信噪比为0 dB时，基于改进的STFT的脉内识别算法的识别概率达到100%，WVD和相位差分算法的识别概率均在97%左右。可见，针对点频输入信号，STFT算法的抗噪性略优于其余两种算法。

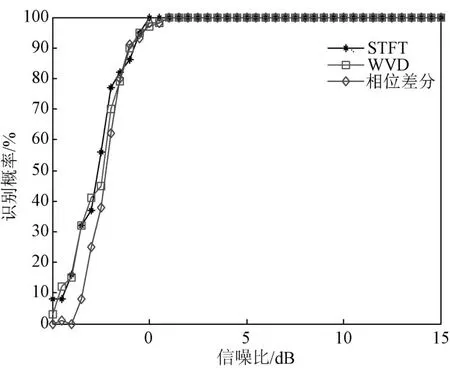
图6 点频信号识别概率

(2)频率调制信号

分别输入LFM、NLFM及频率步进三种频率调制信号，仿真验证了采用不同识别算法时不同频率调制信号的识别概率。仿真结果如图7所示。

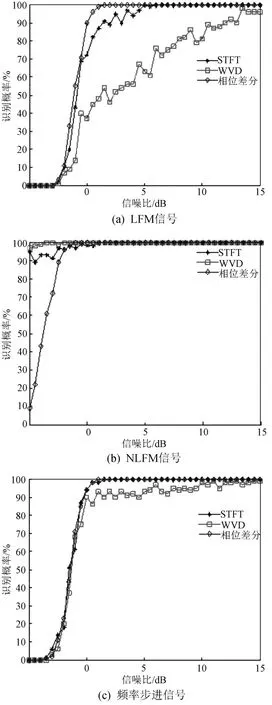
图7 频率调制信号识别概率

LFM信号的识别概率如图7(a)所示。当信噪比达到1.5 d B时，相位差分算法识别概率达到100%；信噪比达到5 dB时，STFT算法识别概率也达到100%；信噪比达到15 d B时，WVD算法识别概率达到97%以上，但仍有波动。由此可见，针对LFM信号，相位差分算法的抗噪性明显优于其余两种算法。

NLFM信号的识别概率如图7(b)所示。当信噪比大于1 dB时，三种算法均能稳定识别输入信号的脉内调制特征；在低信噪比范围内基于WVD的脉内调制识别算法抗噪性最佳，识别概率高达97%以上；改进后的STFT脉内识别算法在0 dB以下低信噪比环境下的识别概率接近90%，且计算量小，易于硬件实现。

频率步进信号的识别概率如图7(c)所示。除WVD算法外，其余两种算法在信噪比大于1.5 dB时已能准确完成脉内调制识别。

(3)相位编码信号

分别输入BPSK和QPSK信号，三种算法识别概率的仿真结果如图8所示。三种算法对两种相位编码信号的识别能力相仿，当信噪比大于1.5 d B时，均能够准确识别信号调制类型。由此可见，针对这两种相位编码信号，三种算法的抗噪性无显著差异，在工程应用上，可以根据实际情况选择合适的分析算法。

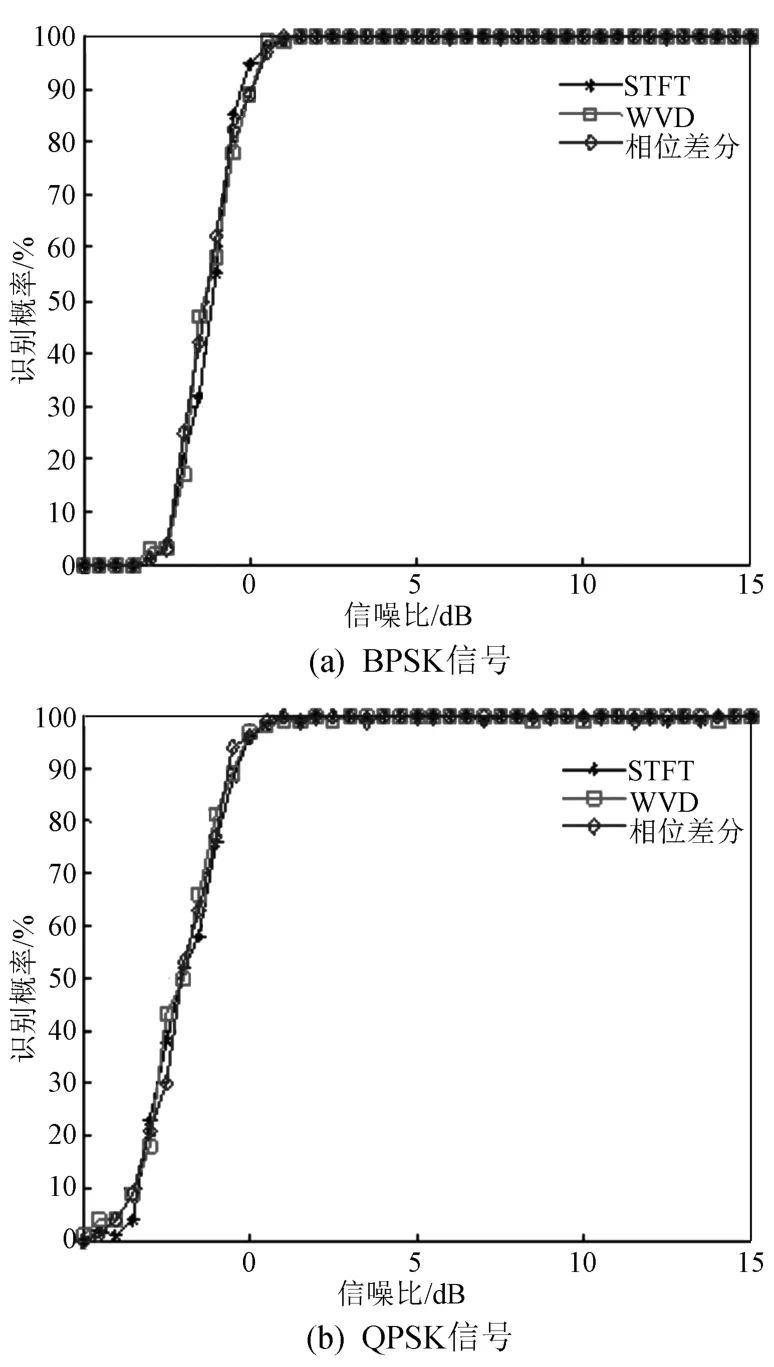
图8 相位编码信号识别概率

(4)频率编码信号

输入两个中心频率分别为900 MHz和910 MHz的FSK信号，三种算法识别概率的仿真结果见图9。在(-5～0)dB低信噪比条件下，改进的STFT算法的识别概率不低于60%。随着信噪比的增高，三种算法的识别概率均增高，当信噪比增高至1 d B时，STFT和相位差分两种算法均能准确完成脉内调制识别，WVD算法的识别概率也达到90%以上。可见，STFT脉内调制识别算法的抗噪性明显优于其他算法，在低信噪比条件下就可以达到不错的识别效果。

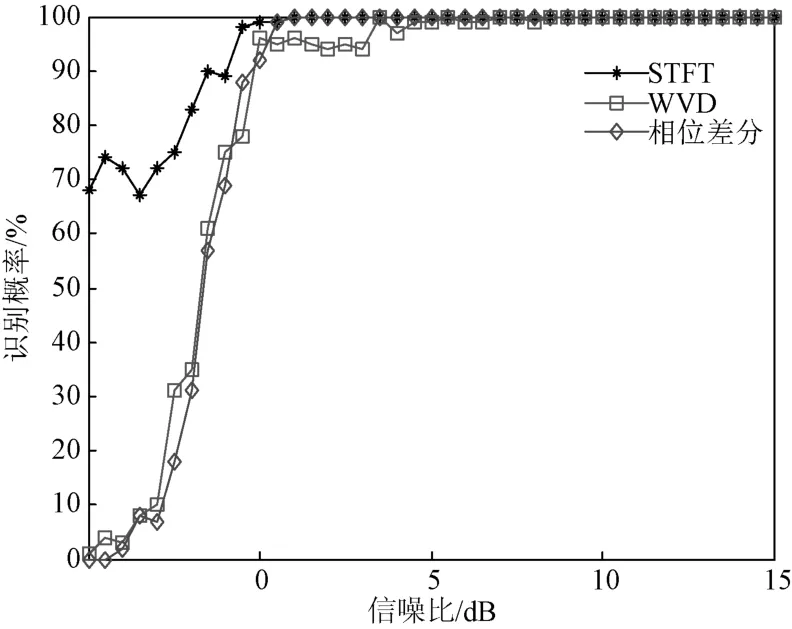
图9 FSK信号识别概率

3.3 时域重叠多信号识别仿真

将七种信号叠加形成一组输入信号，仿真测试三种算法对多信号的识别能力。

设信噪比为10 dB，其他参数设置不变。在该信噪比条件下，叠加信号已经分离，不同类型的信号分布在不同信道中。对每一种脉内调制识别算法进行1 000次的蒙特卡罗实验。仿真结果如表2所示。

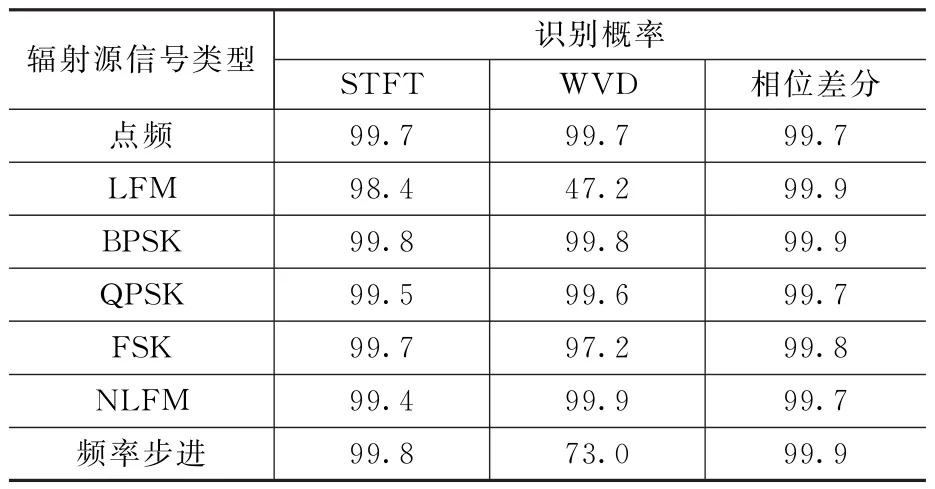
表2 多信号输入蒙特卡罗实验识别概率统计 %

由表2可知，在10 dB信噪比条件下，基于相位差分的脉内调制识别算法的多信号处理能力最佳，对七种调制类型的辐射源信号的识别概率均高于99%。基于STFT的脉内调制识别算法，除LFM信号外，其余信号的识别概率也达到99%以上。基于WVD的脉内调制识别算法，除LFM信号与频率步进信号外，识别概率也高于97%。

4 结论

将基于STFT的脉内调制识别算法进行改进，改进后的算法对LFM、NLFM、频率步进三种频率调制信号的识别概率较改进前有很大提升。当信噪比大于2 d B时，对三种辐射源信号的识别概率均达到90%，对NLFM信号在同一信噪比条件下的识别概率提升超过90%。当信噪比达到5 dB时，识别概率达到99%。

将改进后的STFT算法与WVD和相位差分两种脉内调制识别算法通过仿真实验进行性能的对比分析。基于相位差分的脉内调制识别算法的多信号处理能力最佳，但是该算法计算量相对较大，判断逻辑相对复杂，不利于在FPGA中完成算法实现。WVD算法和改进后的STFT算法是非平稳信号分析的重要手段。三种算法各有优势，可以根据具体需求进行选择。