一种改进小波阈值的图像去噪算法＊

乔林峰 王 俊

（1.陆军军官学院研管大队1队 合肥 230031）（2.陆军军官学院数学教研室 合肥 230031）

1 引言

随着小波理论研究的深入，其应用也日趋广泛，其中，利用小波变换进行去噪始终是一个热点。在图像去噪领域，小波图像去噪方法已成为一个重要的分支和主要的研究方向。目前小波去噪方法大致有三类：第一类是基于小波变换模极大值原理进行去噪；第二类是对含噪声信号作小波变换之后，计算相邻尺度间小波系数的相关性，根据相关性区别小波系数的类型，进行取舍，然后重构信号；第三类是小波阈值去噪方法。上述三类去噪方法中最早被提出的是小波阈值去噪方法，它是一种实现简单而且效果较好的去噪方法。本文对其阈值函数进行了改进，通过实验仿真，其能较好地保留图像的边缘细节信息，去噪效果很明显。

2 小波阈值去噪的基本原理

1）理论依据

设有含噪模型：f（k）＝s（k）＋n（k），k＝0，1，2，…，N－1，其中，s（k）为原始图像信号，n（k）为方差为σ2，服从 N（0，σ2）分布的高斯白噪声。

对f（k）作离散小波变换得：wj，k＝Ws（j，k）＋Wn（j，k），j＝0，1，2，…，J；k＝0，1，2，…，N其中，ωj，k，Ws（j，k）和 Wn（j，k）分别为含噪图像，原始图像和噪声信号在第j层上的小波系数；J和N 分别为小波变换的最大分解层数和图像的总像素数。由小波变换的线性性质知，对f（k）作离散小波变换后，得到的小波系数wj，k，仍然由两部分组成，即原始图像s（k）对应的小波系数Ws（j，k），记uj，k，和噪声信号n（k）对应的小波系数 Wn（j，k），记vj，k。

小波阈值去噪的主要理论依据为：有用的图像信息表现为低频信号或是比较平稳的信号，而噪声信号则表现为高频信号。因此经小波分解后，信号的小波变换系数要大于噪声的小波变换系数。于是可以找到一个合适的数作为阈值（门限），当 wj，k小于该阈值时，认为这时的 wj，k主要是由噪声引起的，可将其置为零；当wj，k大于该阈值时，认为这时的wj，k主要是由信号引起的，可对其进行保留或收缩，从而实现了信噪的分离。

2）具体步骤

（1）含噪声图像的小波分解。对含噪图像信号f（k）进行离散小波变换，得到各尺度小波系数wj，k。

（2）小波分解高频系数的阈值处理。对各尺度小波系数wj，k进行阈值处理，得出估计小波系数＾wj，k，使‖＾ωj，k－uj，k‖尽可能的小。

（3）图像的小波重构。利用＾wj，k进行小波重构，得到含噪图像信号f（k）的估计信号＾f（k），即为去噪后的信号。

3）阈值函数的选取

最常用的阈值函数有硬阈值函数和软阈值函数两种。

（1）硬阈值函数：

（2）软阈值函数：

其原理图如下：

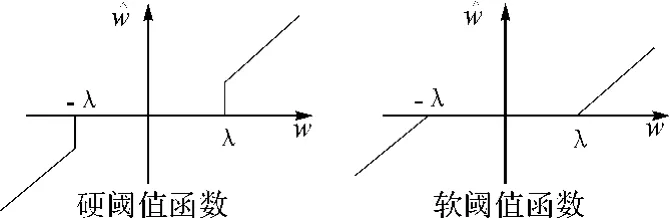
图1 硬、软阈值函数

硬阈值和软阈值函数虽然在实际中得到了广泛的应用，也取得了比较好的去噪效果，但这些方法本身还存在着一些潜在缺陷。利用硬阈值方法进行图像处理，得到的估计小波系数值连续性差，即在±λ处是不连续的，利用进行重构得到的图像可能会产生振荡、Gibbs效应（截断效应）等视觉失真；而利用软阈值方法估计出的小波系数虽然整体连续性很好，但是由于当小波系数较大时，即当时和 wj，k之间总会存在恒 定的偏差，这将会直接影响重构图像和真实图像的逼近度，给重构图像带来不可避免的误差。另外，传统的软阈值函数导数不连续，然而在实际的应用中经常要对一阶甚至是高阶导数进行运算处理，所以其具有一定的局限性。

3 改进的小波阈值算法

本文根据上述两种函数的不同优点，结合斜坡阈值技术［10～11］（Ramp threshold function），提出了一种新的阈值函数，用于小波系数的估计运算，其计算公式如下：

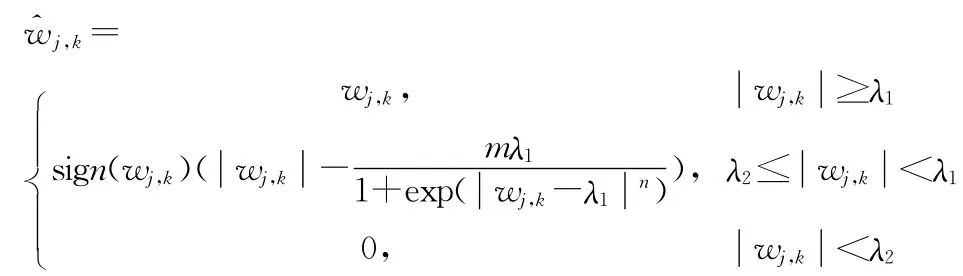
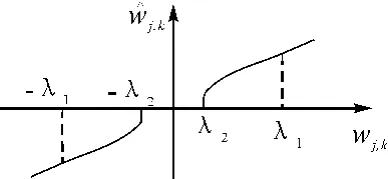
图2 新阈值函数（m＝1／2，n＝3）

改进后的阈值函数（取m＝1／2，n＝3）如图2所示。

由以上表达式和原理图可知，该函数有以下几个特点：

（3）具有与软阈值函数相同的连续性。

g利用了斜坡阈值技术，可以有效地克服Gibbs效应。

4 算法流程

本文改进小波阈值算法的流程图见图3，具体步骤如下所示：

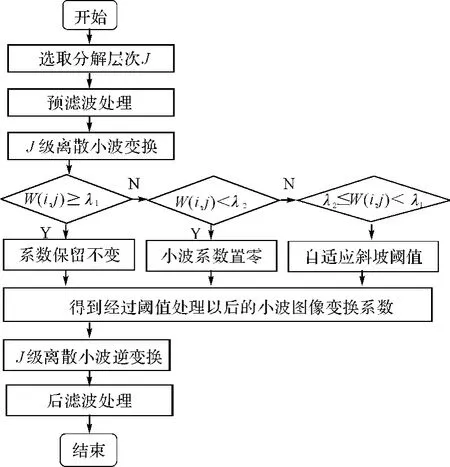
图3 改进小波阈值算法流程图

5 仿真实验结果与分析

下面采用噪声方差为0.01的高斯白噪声，以lena512×512图像为例，为了验证改进小波阈值算法的去噪效果，选取SYM4小波对含噪图像进行三层分解，然后分别用软阈值函数，硬阈值函数和本文提出的改进的阈值函数计算小波系数，再用SYM4小波进行重构，得到去噪图像。

图4是以lena512×512图像为例的实验结果，从图4（e）可以看出图像的含噪量得到明显地减少，并且能够很好地保留图像的纹理细节。

图4 lena图像去噪结果

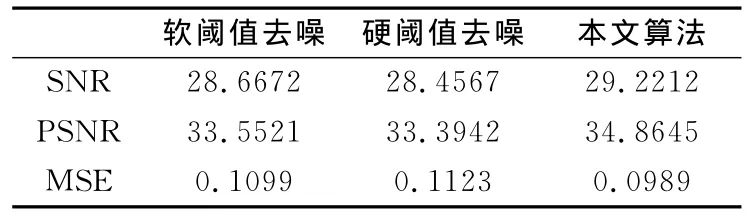
表1 lena图像去噪结果比较

从表1的数据可以看出，本文提出的算法与传统的软、硬阈值方法相比，均方误差MSE明显下降，信噪比SNR和峰值信噪比PSNR方面都有明显的提高，能够较好地保留图像的边缘和细节信息，去噪效果很好。

6 结语

本文介绍了小波阈值去噪的基本原理以及软、硬阈值方法去噪的优缺点，并结合斜坡阈值技术提出了一种改进小波阈值的图像去噪新算法。仿真实验表明：该算法对图像进行去噪，得到了较低的均方误差和较高的信噪比，并且有效地去除了Gibbs效应，保留了较多的边缘和细节信息，达到了很好的去噪效果。

［1］程正兴.小波分析算法与应用［M］.西安：西安交通大学出版社，2004.

［2］姚敏.数字图像处理［M］.北京：机械工业出版社，2006.

［3］高志，余啸海.小波分析与应用［M］.北京：国防工业出版社，2007.

［4］贾杏托.基于多小波变换的图像降噪算法的研究［D］.［燕山大学硕士学位论文］.2009：40－44.

［5］栗艳艳.基于小波变换和偏微分方程的图像去噪算法研究［D］.［西安理工大学硕士学位论文］.2010：18－24.

［6］游林儒，谢俊斌.基于邻域多样本系数估计的小波图像去噪［J］.计算机与数字工程，2008（3）.

［7］姚晋丽，王霞.一种基于小波变换的显微图像去噪算法研究与实现［J］.计算机与数字工程，2008（7）.

［8］唐琳，晏海华，蔡德荣，等.一种基于最优小波包基的图像去噪算法［J］.计算机与数字工程，2008（4）.

［9］Tien D.Bui，Guangyi chen.Translation－Invariant Denoising U－sing Multiwavelets［J］.IEEE Transactions on Signal Processing，1998，46（12）：3414－3420.

［10］P.M.Patil，T.R.Sontakke.Rotation，scale and translation invariant handwritten Devanagari numeral character recognition using general fuzzy neural network［J］.Pattern Recogntion，2007，（40）：2110－2117.

［11］Say Song Goh，Qingtang Jiang，Tao Xia.Construction of Biorthogonal Multiwavelets Using the Lifting Scheme［J］.Applied and Computational Harmonic Analysis，2000，（9）：336－352.

［12］Tai－Chiu Hsung，Daniel Pak－kong Lun.Optimizing the Multiwavelet Shrinkage denoising［J］.IEEE Transcations on Signal Processing，2005，53（1）：240－250.

［13］T.R.Downie，B.W.Sliverman.The Discrete Multiple Wavelet Transform and Thresholding Methods［J］.IEEE Trans.Signal Process，1998，（46）：2558－2561.