基于覆盖算法概率模型的海量数据挖掘研究＊

李其芳

（陆军军官学院 合肥 230031）

1 引言

覆盖算法是一种构造性的神经网络学习算法，它根据数据自身的结构，构造性地建立了神经网络模型。构造性神经网络可分层逐步构造，网络的基本功能被划分成若干独立的功能模块。各模块独自负责解决问题的一部分，因此在学习阶段所处理的数据也不完全相同。其有如下特点：

1）构造性的网络结构中各功能模块相对简单，各模块主要是集中于问题的一部分，所要解决的问题也相对简单，不会受到各种不同信号的影响，因此容易训练，相对简单的网络结构提高了网络的泛化能力；

2）各功能模块相对独立，可并行地进行训练，训练效率高；

3）网络的行为便于解释、分析，网络的设计容易改进；

4）硬件更易实现，因为构造若干简单的模块再将它们连接起来比建立全连接的大规模网络更容易。

构造性神经网络将无限大的划分区域变换为有限的划分区域，通过非线性变换，将学习问题变为划分问题，将多区域相交复杂性简单化，可以实现多类别样本的同时划分；将神经元的功能局部化，将非局部性的划分区域变换为局部性划分区域，故其计算量少，速度快，能实现海量的模式分类。

2 覆盖算法的概率模型

2.1 概率有限混合模型

在概率论中有如下的命题成立：任何连续分布均可由等方差高斯密度的有限混合任意逼近。也就是说，在近似的意义下，只要研究有限高斯混合密度就足够了。通过这种思想，可以利用有限高斯混合密度为覆盖算法建立概率模型。

2.2 有限混合模型的定义

设X1，…，Xp是样本量为p的独立同分布随机样本，其中Xi是n维随机向量，其概率密度函数为f（x）。设f（xi）可表示成：

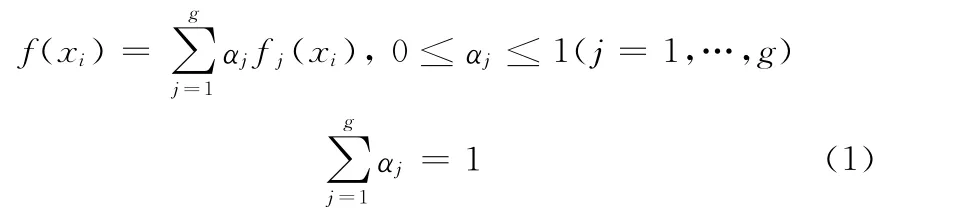
其中fj（xi）表示观察值xi来自第j分量时的条件概率密度函数。

若取fj（x）为1维高斯分布，则上式可表示成：

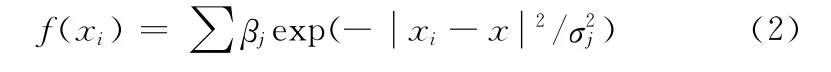
3 覆盖算法的概率模型的实现

设给定分类问题，即共有p个n维样本，分成m类。

简单的覆盖算法，对每个覆盖取特征函数来表示，这种表示未能反映样本在覆盖中的分布情况。高斯分布函数可以克服这个缺点，若对每覆盖引入高斯核函数（以覆盖的中心为高斯核函数的均值，取半径为方差，记为对应于第i类的决策函数为

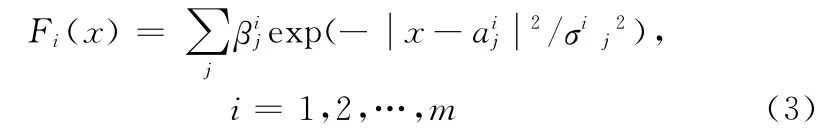
上式又可以理解为高斯函数的覆盖算法得到的决策函数。从上面一系列变换后，使我们可以从概率的角度来考察它，因为式（3）可以看成是一个有限混合概率模型，于是可以利用最大似然的算法，求得式（3）的最优参数。这样就从概率角度为函数的确定参数问题，给出一个合理的解决方法。于是可将概率统计中现成的方法引入分类学习，也就是把覆盖算法与统计模型结合起来，为覆盖算法找到全局优化的途径。

4 基于覆盖算法的概率模型的海量数据挖掘算法

给定m类分类的训练样本集K＝｛K1，K2，…，Km｝，算法实现具体步骤如下：

1）利用覆盖算法，求出各类的覆盖组｛C1，C2，…，Cm｝：

（1）将所有的点投影到Sn上（中心在原点，半径为R，R＞max（｜xl｜），l＝1，2，…，p），仍记为 K1，K2，…，Km；

（2）若K1（开始时i＝1）非空，作一覆盖，i＝1，2，…，m，j＝1，2，…，gi，它只覆盖K1的点，被覆盖Ki的子集为Kij（j＝1，2，…，gi）；

（3）若 Ki被覆盖完，i＝i＋1，若i＞m，则转至（8），否则，任取Ki中尚未被覆盖的一点ai；

（5）求C（ai）所覆盖点的重心，将其映射到球面上，设投影点为a′i，按（4）中公式求θ′i，求得球形领域C（a′i）；

（6）若C（a′i）所覆盖的点数大于C（ai）所覆盖的点数，则令a′i→ai，θ′i→θi，返回（5），否则，得到C（ai）的一个覆盖，转到（7）；

（7）求ai的平移点a″i，并求对应的球形领域C（a″i），若C（a″i）覆盖的点数大于C（ai）所覆盖的点数，转到（5），否则，得到C（ai）的一个覆盖，转步（3）；

（8）样本学习结束，得到覆盖组。

2）以覆盖的中心为高斯核函数的均值，取半径为方差，对每覆盖引入高斯核函数；

4）利用文献［7］中给出求解最大似然的迭代EM算法进行最大似然拟合。

利用EM方法求解最大似然问题，难点在于如何合理地选取混合模型的分量个数问题（这就像k－均值法中如何取k的问题）。对覆盖算法，这个问题可利用覆盖算法求得的覆盖，作为EM算法的迭代起始值，得到很好地解决。因为利用覆盖算法求得的覆盖组，基本已是次优的覆盖，在此基础上再利用EM算法进行迭代就能很快求到最优解。这也是对覆盖算法的概率模型引入“最大似然原则”成功的所在。

另外需要说明的是，为了防止迭代过程发散，对出现下面情况进行调整：

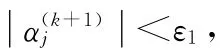
3）给定ε2，对＜ε2的覆盖Cj，将覆盖Cj保留，下一轮迭代时对该覆盖不进行迭代，防止EM迭代的发散，因为方差很小的覆盖，所覆盖的点多是“离群点”。

给出一个迭代停止的条件（如达到一定迭代精度或达到一定的迭代次数），最后迭代停止时所得到有限概率模型即所求。

5 实验与结果分析

实验将基于覆盖算法的概率模型的海量数据挖掘算法应用到短波无线电监测中以验证数据挖掘的效果。

无线电监测的目的是维护电台活动秩序，及时发现非法电台。一般说辖区内合法电台的用频、工作时间等都是经过政府认可的，我们可以此为依据发现非法电台。然而，短波信号通过天波传播，传播距离远，在检测无线电信号时，能截获大量信号数据，容易受到其他国家和地区通信电台的影响，噪声比较多，信号很密集，要处理的数据量相当大。

本实验分成三个部分：一是调谐接收机，采集信号作为分析数据；二是将采集信号的前一部分作为训练样本，利用覆盖算法的概率模型进行聚类；三是用后一部分信号数据作为测试样本检验基于覆盖算法的概率模型的海量数据挖掘算法的挖掘效果。

本实验通过计算机遥控某种型号的短波接收机，使其在15MHz～16MHz频段内，按照5kHz步进，从低到高循环搜索，3分钟为一个周期，搜索到任一频点（第i频点频率为（15001.5＋5*i）kHz，i＝0，2，…，332），驻留一短暂的时隙（如70ms），此时从接收机的中频输出端采集信号并存入数据库或直接分析。接收机的中频输出频率是200kHz，带宽设置为3kHz，采用带通采样，采样频率为10.24kHz。采集的数据是时域数据，不便分析，被采样的时域数据经快速傅立叶变换（FFT）转化为频域数据存入数据库，等采集样本达到一定的数据量时再进行处理。利用部分被采集的数据作为训练样本，构建神经网络，再用另一部分数据（如一天的数据）作测试样本。

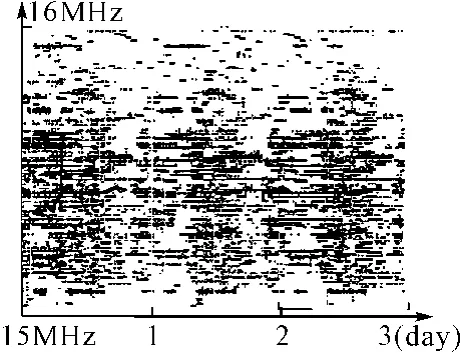
图1 所采集信号频占图

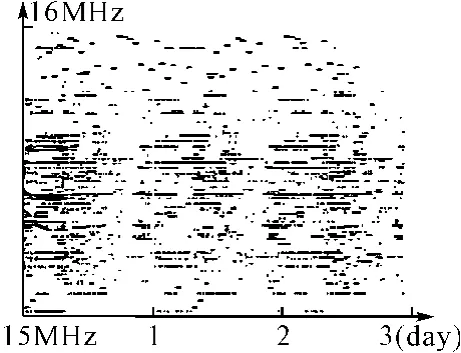
图2 经过算法处理后的信号频占图

图1是15MHz～16MHz频段内连续3天被截获信号的频占图（约1.44×106个数据点），横轴代表时间，纵轴代表频率，图1中点的虚实代表该点对应的时间和频率上有无信号。图1中存在一个跳频信号，它是在实际频率占用度基础上，利用频率间隙嵌入跳频信号。这样模拟的数据比单纯模拟的数据更加符合实际情况。它的频率集包含31个频率点，但是由于信号环境复杂，包含其他电台信号、噪声干扰等信息，跳频信号频率集不容易被提取。

为了有效地获取知识，对图1所示数据进行预处理，经算法处理，剔除干扰、过滤噪声后，频率占用度如图2所示，绝大部分噪声被有效地滤除。

利用覆盖算法的概率模型得到的改进覆盖算法，并与原覆盖算法、核覆盖算法进行挖掘，得到表1所示的结果。

表1 不同方法实验结果表

从表1得出，利用改进覆盖算法对无线电监测数据进行挖掘，挖掘所用时间和正确率比原覆盖算法和核覆盖算法都提高了，这是由于改进的算法从全局出发，对所有测试样本都能到达最优。

6 结语

本章从大规模数据挖掘的角度出发，分析了传统神经网络的不足，在M－P神经元几何意义的基础上，介绍了覆盖算法的原理及其经典算法，即领域覆盖算法和交叉覆盖算法；然后简单介绍了核覆盖算法，并在核覆盖算法的基础上，利用高斯函数的概率意义（高斯分布），为核覆盖算法建立一个有限混合概率模型，提出了覆盖算法的概率模型，对覆盖算法进行改进，给出了一种新的算法，即基于覆盖算法的概率模型的海量数据挖掘算法；利用这种改进的算法构造的神经网络，在保持计算复杂度不变的前提下，引入全局优化计算，扩大了覆盖算法的使用范围，提高了算法的精度，适合大规模数据挖掘。最后的实验验证了算法的实效性。

［1］张铃，张钹.多层反馈神经网络的FP学习和综合算法［J］.软件学报，1997，8（4）：252－258.

［2］张莉.SVM与核方法研究［D］.西安：西安电子科技大学，2002.

［3］赵姝，张燕平，张媛，等.基于交叉覆盖算法的入侵检测［J］.计算机工程与应用，2005（1）：141－143.

［4］张燕平，张铃，段震.构造性核覆盖算法在图像识别中的应用［J］.中国图象图形学报，2004，9（11）：1304－1308.

［5］张旻，陈加兴.基于粒度计算和覆盖算法的信号样式识别［J］.计算机工程与应用，2003（24）：56－59.

［6］王伦文，张铃，张旻.一种适合于无线电监测的数据挖掘技术［J］.计算机工程与应用，2004（4）：37－40.

［7］张立斌，高仲春.基于遗传算法的数据挖掘维度选择［J］.计算机与数字工程，2012（5）.

［8］周义建，王轶，王辉.基于Apriori数据挖掘优化方法研究［J］.计算机与数字工程，2008（2）.

［9］Dempster A P，Laird N M，Rubin D B.Maximum likelihood from incomplete data using the EM algorithm（with discussion）［J］.R.Stat.Soc.Ser.B，1977：1－38.

［10］Heckman D，Geiger D，Chickering D.Learning Bayesian networks：the combination of knowledge and statistical data［J］.Machine Learning，1995，20（3）：197－243.

［11］Heckman D，Mandani A，Wellman M.Real－World applications of Bayesian networks［J］.Communications of the ACM，1995，8（3）：38－45.

［12］Heckerman D.Bayesian networks for data mining［J］.Data Mining and Knowledge Discovery，1997：79－119.