基于内插的符号同步算法设计＊

田丽娟 杨 平

（中国船舶重工集团公司第七二二研究所 武汉 430079）

1 引言

在数字通信系统中，符号同步不仅要求准确检测到数据的起始位置，还需要确定在每个码元间隔的什么时刻以符号速率进行周期性地采样和判决，符号同步算法的优劣对降低接收端的误码率起到了至关重要的作用。对于数据起始位置的确定一般是通过集中插入特殊的训练序列，利用局部自相关函数的单峰特性来识别同步头。在码元周期间隔内，最佳采样时刻由信号波形决定，可能位于码元中间时刻，也可能是码元起始时刻或终止时刻，实际可行的方法层出不穷，如传统的锁相环法、早迟门同步法、Gardner算法［1］、数字滤波平方算法［2］、内插估值法［3］等。其中，内插估值法源于数值分析中多项式插值的思想，是指利用定时误差来控制内插滤波器［4～5］对采样数值进行某种插值运算，以使其逼近最佳采样时刻的信号值。

本文首先针对数据起始时刻的确定，提出一种能有效降低虚警概率的多同步头联合检测算法，并通过Matlab仿真比较其性能。接着简要介绍通常所用的内插估值方法的基本原理。最后讨论一种基于最大似然估计的等分内插逼近法，并在存在一定频偏的情况下，通过Matlab仿真讨论分析了过采样数及训练序列长度对误码性能的影响。

2 同步头联合检测方法

通常数据以帧为基本单位进行传输，对于数据起始位置的确定一般是集中插入特定的训练序列，利用其具有尖锐单峰特性的局部自相关函数来判别。为了提高正确检测概率pc和降低虚警概率pf，可以增长训练序列长度，但同时传输的开销会增大，使得传输信息的有效性降低。在确定同步头长度时，需要兼顾检测的可靠性和传输的有效性，两者折中处理，一般同步头长度选取为数据长度的5%～10%较为合理［6］。 鉴 于 此，提出了多同步头联合检测的算法，其原理如图1所示。

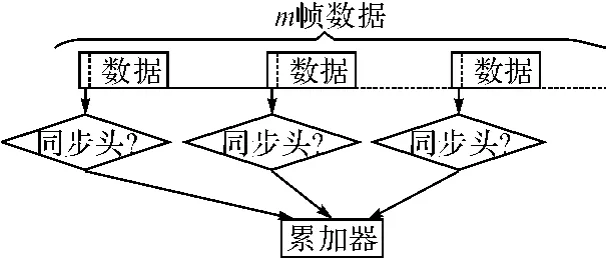
图1 多同步头联合检测示意图

其具体做法是对于连续m帧数据，将每帧数据的同步头提取出来，并行检测这m帧数据内总共能识别出多少个同步头，将累加结果与一预先设定的门限值Nth进行比较，这种做法可以在不增加每帧数据同步头长度的前提下大幅度提高检测的可靠性。

对于单个同步头检测方法，作如下性能仿真：

在误码率p＝0.1的条件下，同步头为8个比特码元，通过仿真得出pc、pf相对于门限值的性能曲线如图2所示。

对于多个同步头联合检测方法，作如下性能仿真：

在误码率p＝0.1的条件下，同步头为8个比特码元，单同步头检测的判决门限设为6，检测的数据帧数m设为16，则通过仿真得出pc、pf相对于门限值的性能曲线如图3所示。

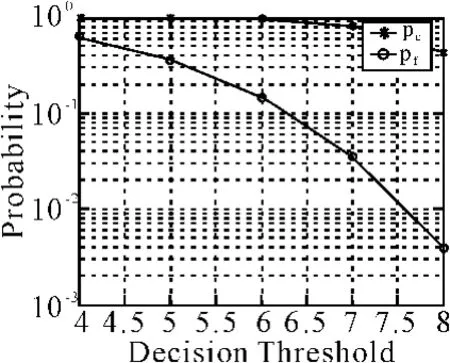
图2 单同步头检测

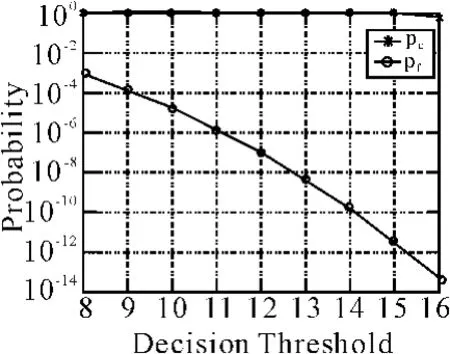
图3 多同步头检测

比较原始的与改进后的仿真结果：图3相对于图2，其正确检测概率pc随着门限值Nth增大有明显提高，而虚警概率pf随着门限值Nth增大大幅度降低。由此可得出如下结论：多同步头联合累加检测算法的检测性能明显优于单一同步头检测方法。

3 内插估值的基本原理

内插的基本思想是接收端采用独立于码元周期T的固定采样时钟周期Ts采样，正确的定时样值点是通过对连续几个采样点做插值计算得到的近似值，如图4所示：样值点kT的值是通过对（mk－1）Ts，mkTs，（mk＋1）Ts，（mk＋2）Ts这四个原始采样值作内插运算获得的。其中mk称为基本指针，用于决定参与计算内插值R（kT）的信号样点集；uk称为分数间隔，用于指示内插估值点并用来确定内插滤波器的样点值［7］。

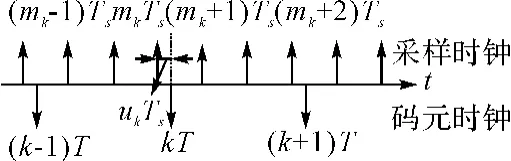
图4 固定采样点与定时样值点关系图

数字内插滤波器的基本方程为

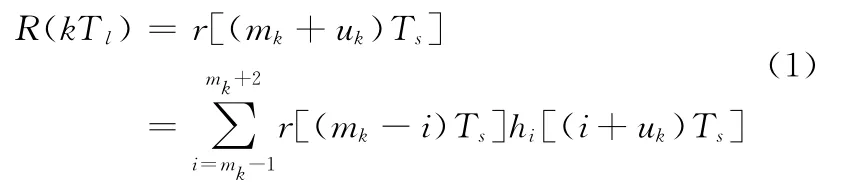
式（1）中uk的提取是有效实现准确内插同步的关键，通常由NCO控制器来完成。每次进行内插运算时，都需要根据不同的uk值来更新内插滤波器的系数。

4 最大似然估计

4.1 最大似然估计原理

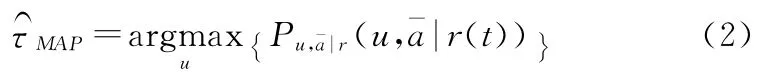
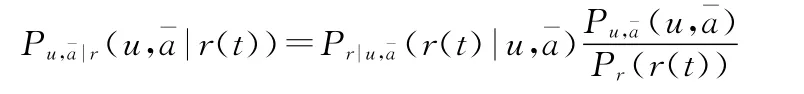
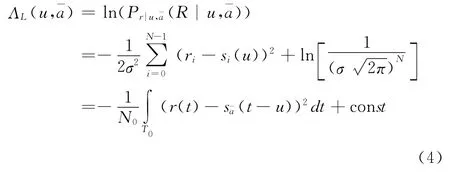
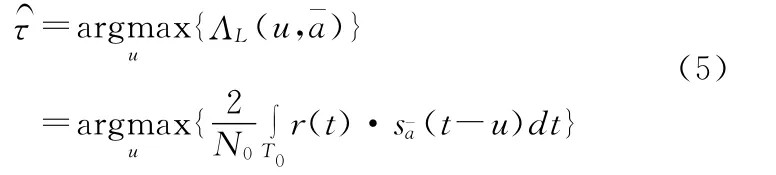
4.2 最大似然估计器

基于判决修正方法（DD）的最大似然误差估计是利用数据符号的估计来使定时估计的似然函数最大化，其数学表达式如式（6）：

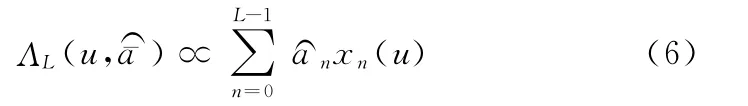
基于非判决修正方法 （NDD）的最大似然误差估计的数学表达式：

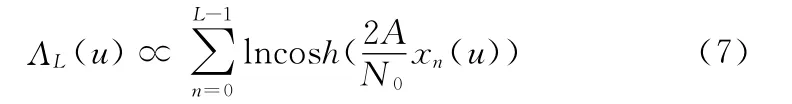
文献［9］给出了式（7）两种非线性替换形式：一种采用绝对值近似的非线性形式（AVN）：

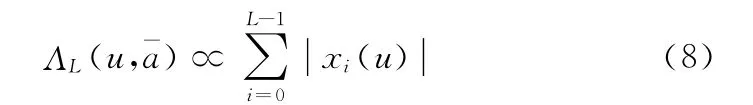
另一种采用平方率近似的非线性形式（SLN）：

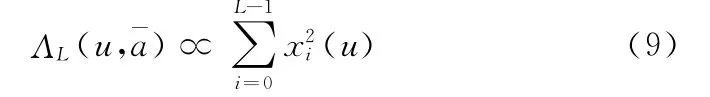
文献［10］给出了另一种非线性形式（FLN）；

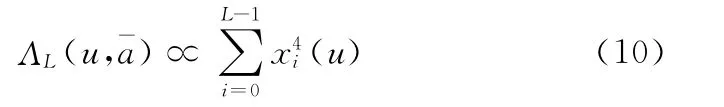
5 内插逼近方法

5.1 基本原理及实现步骤

采用基于判决修正方法（DD）的最大似然估计，即运用式（6）计算ΛL。等分内插逼近法的具体步骤归纳如下：

1）将接收信号经过匹配滤波器后以K倍速率进行采样，在一个符号周期内得到K个采样值分别为x（1），x（2），…，x（k），逐个计算每个样本的似然函数值ΛL，找到较大的两个ΛL值所对应的样本值，分别标示为x1（a）和x1（b）。从理论上讲，在一个符号间隔内以两倍的符号速率采两个样值，只要保持这两个样值分别位于峰值两侧即可实现逐次内插逼近最佳定时时刻。当内插逼近次数n＝1时，取x1（a）和x1（b）等分点，记为x1（c）；

2）当内插逼近次数n＝2时，在完成1）的基础上，计算x1（a）、x1（b）和x1（c）的似然函数值ΛL，找到较大的两个ΛL值，例如此时x1（b）和x1（c）的ΛL值较大，则将x1（b）标记为x2（a），x1（c）标记为x2（b），再取这两个值的等分点得到最佳定时位置，记为x2（c）；

3）当内插逼近次数n＝3时，完成上述1）2）后，计算x2（a）、x2（b）和x2（c）的似然函数值ΛL，找到较大的两个，依次标记为x3（a）和x3（b），再在这两个值之间进行等分内插得到最佳定时位置x3（c）；

当n＞3时，重复执行步骤3）即可。由上述逐次内插逼近的步骤可知，最佳定时位置的精确度主要由逼近的次数n决定。经观察得出：逼近次数n与相邻估值点的间距Δ的关系为：Δ＝2－（n＋2）T，n＝1、2、…。所以，当逼近次数n＝4时，定时同步可达到的精度为码元周期的1／64，此时计算似然函数的总次数为n＋1＝5，其运算量仅等价于对5个采样点进行似然函数计算，通常达到同样的精度则需要对64个采样点的似然函数都进行计算并作比较。于是可看出此算法在取得同样定时精度的情况下，能明显减少运算量。

5.2 仿真结果与分析

使用matlab软件对本算法进行仿真分析，仿真参数设置如下：

目标价格水平发生变化时，上述市场均衡会发生一系列反应从而达到新的均衡。根据Muth和Gardner的方法，我们将上述结构模型进行全微分，并利用克莱姆法则将其求解后得到模型的最终形式，即外生变量变化引起的内生变量变化率。

调制方式：GMSK（同样也适用于MSK、MPSK等其他调制方式）；

滤波器：发送端高斯低通滤波器BT＝0.3，接收端高斯低通滤波器BT＝0.5（如选用其他调制方式，如MPSK，可选用升余弦根滤波器）；

载波频率：正弦载波fc＝2800Hz；

符号速率：f＝3200bps；

过采样因子：K＝8、16，即抽样频率fs＝Kf；同步头长度：L＝32、256；

频偏：Δf＝70Hz；

所加噪声：加性高斯白噪声；

逼近次数：n＝4（相当于每个符号过采样64个样值点）。

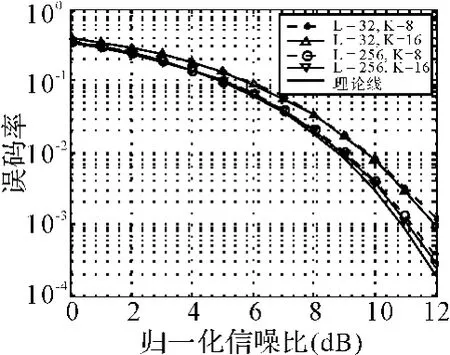
图5 Δf＝70Hz，L＝32和256时过采样数K对误码率的影响

采用基于判决修正方法（DD）的最大似然估计方法，仿真结果如图5所示。

不难发现：过采样因子K和同步头长度L的增大都会使误码率降低，但对于相同长度的同步头，过采样数K的增加，对误码率性能改善并不大，而该性能更多的是受同步头长度的影响。运用此方法时，提高过采样率对提高定时同步的精度意义并不大，可以通过不断增加内插逼近次数来获得更好的误码性能。

6 结语

本文提出的符号同步算法具有性能优良，算法高效，实现简单的特点。运用多同步头联合累加检测方法，能更加有效地提高正确检测概率，同时具有良好的数据传输开销；此同步头同时作为训练序列，利用最大似然估计的思想，通过等分内插逼近的方法准确找到每个码元内的最佳采样时刻，只要内插逼近的次数足够多，就能达到满意的误码性能。

［1］Gardner F M.Interpolation in digital modems–part I：Fundamentals［J］.IEEE Transaction On Communications，1993，41（3）：501－507.

［2］Martin Oerder，Heinrich Meyr.Digital filter and square timing recovery［J］.IEEE Transaction On Communications，1988，36（5）：605－612.

［3］Cowley W G，Sabel L P.The performance of two symbol timing recovery algorithm for PSK demodulators［J］.IEEE Transaction On Communications，1994，42（6）：2345－2355.

［4］Vesma J，Saramaki T.Interpolation Filters with Arbitrary Frequency Response for all digital Receivers［J］.IEEE Int.Symp，1996：568－571.

［5］Jaume Riba.A Performance Lower Bound for Quadratic Timing Recovery Accounting for the Symbol Transition Density［J］.IEEE Transactions on Signal Processing，2004，52（11）：3278－3288.

［6］侯战斌.数字化鉴频与位帧同步技术研究［D］.北方工业大学，2007：19－20.

［7］Lays.Erup F M，Gardner R A，Harris.Interpolation in digital modems－Part II：Implementation and Performance［J］.IEEE Transaction On Broadcasting，1993，41（6）：998－1008.

［8］肖珑矫.突发通信中接收机的定时同步技术研究［D］.哈尔滨工程大学，2005：28－29.

［9］Ging Liu，Che Wei.Timing recovery techniques for digital cellular radio with pi／4DQPSK modulation［J］.Processing of ICC－92，1992：190－196.

［10］Andrea N D，Mengali U.A simulation study of clock recovery in QPSK and 9QPRS systems.IEEE Transaction On Commu－nications，1985，10：1139－1142.