水污染防治问题的数学模型研究＊

夏必腊 沈 浮 王 鹏 李文涛

（解放军陆军军官学院数学教研室 合肥 230031）

1 引言

由于自然条件的影响，水资源特别是淡水资源在全球上分布不均，而且受气候变化的影响，使许多国家和地区可用量减少。目前，世界范围内城市和工业区集中发展，由于集中用水很大，超过当地水资源的供水能力，城市生活和工业用水存在大量的浪费和盲目开采造成水资源不足。另外，加上水体污染日趋严重，这样原本地球上极其丰富的水资源面临严重危机。根据相关资料统计，目前全世界每年约4200多亿立方米的污水排入江河湖海，污染了5500亿立方米的淡水，约占全球净流量的14%以上。河流污染已经影响到人类的正常生活和生存，因而研究污染物在水体中的扩散现象及其扩散规律是治理和控制水体污染的重中之重，对河流水质的监测保护以及水资源的合理使用有着重要的意义。

本文针对河流水质的模型，从数学角度加以解释分析，最后提出河流水质模型在实际应用中的意义。

2 水污染问题的数学模型

假设有一稳定流的一维均匀河段，已知弥散系数D＝2km／h，流速v＝5km／h，某污染的一级反应速率常数k＝0.015km／h，在x0＝0处有一点源，连续排放1小时，若起始断面处在排放期间某污染物的浓度为＝10mg／L（j＝0，1，…，m），tm为排放终止时间，在河段的其它断面处＝0（i＞0）。要求在8km长的河段里，从开始排放污染物起，不同时间，不同地段污染物的浓度分布。

考虑河流的一般流动状态，除了考察分子的扩散与湍流扩散外，还要考虑到由剪切流造成的类似分子扩散的弥散作用。但在天然河流中，分子扩散系数具有数量级10－5～10－4m2／s，湍流扩散系数具有数量级10－2～1m2／s，而弥散系数的数量级为10～103m2／s，因此，在河流水质模型中，一般可以忽略分子扩散及湍流扩散的影响，只须考虑弥散作用，于是可建立如下微分方程［4］：

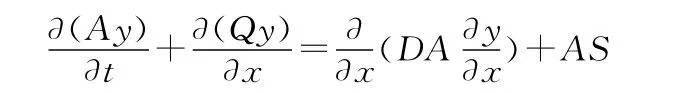
其中，A为河床断面（L2）；Q 为流量（L3T－1）；D 为弥散系数（L2T－1）；y为某组分子在x 断面处t时刻的浓度（ML－3）；S为各种源和汇的代数和。

对于一个不太长的河段，常可假定其水流近似地处于稳定状态，断面沿程均匀。这样A、Q、D都可近似地作为常数处理，于是上述微分方程可简化为

若河流中某种污染物进行一级衰减反应，并假定河底无渗漏，忽略面源的侧向输入，这时S＝－ky，k为常数。在不太长的河流中，某一污染物扩散所满足的微分方程是一抛物型方程，结合实际问题的假设，可得到如下定解问题：

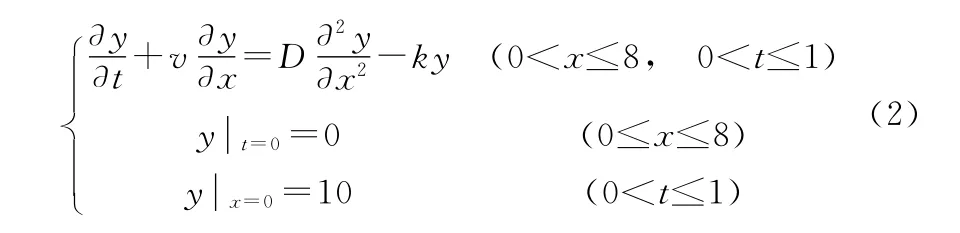
3 水污染方程的求解方法

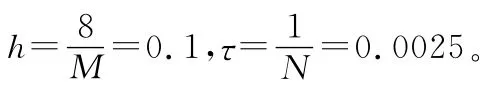
对于其中的三个一阶偏导数分别用相应的差商代替，即令

代入式（3），可建立如下显式差分格式［9］：

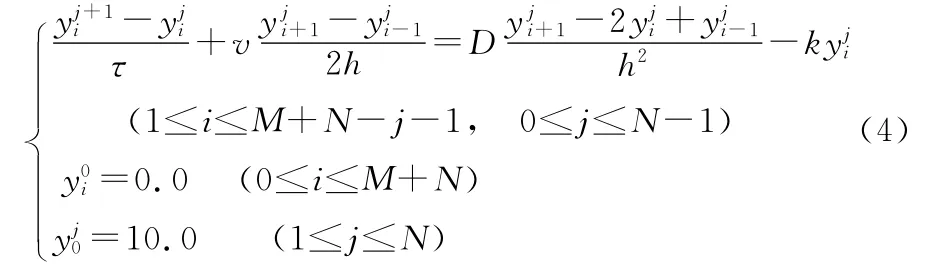
当取参数v＝5，k＝0.015，D＝2时，计算结果列于表1。

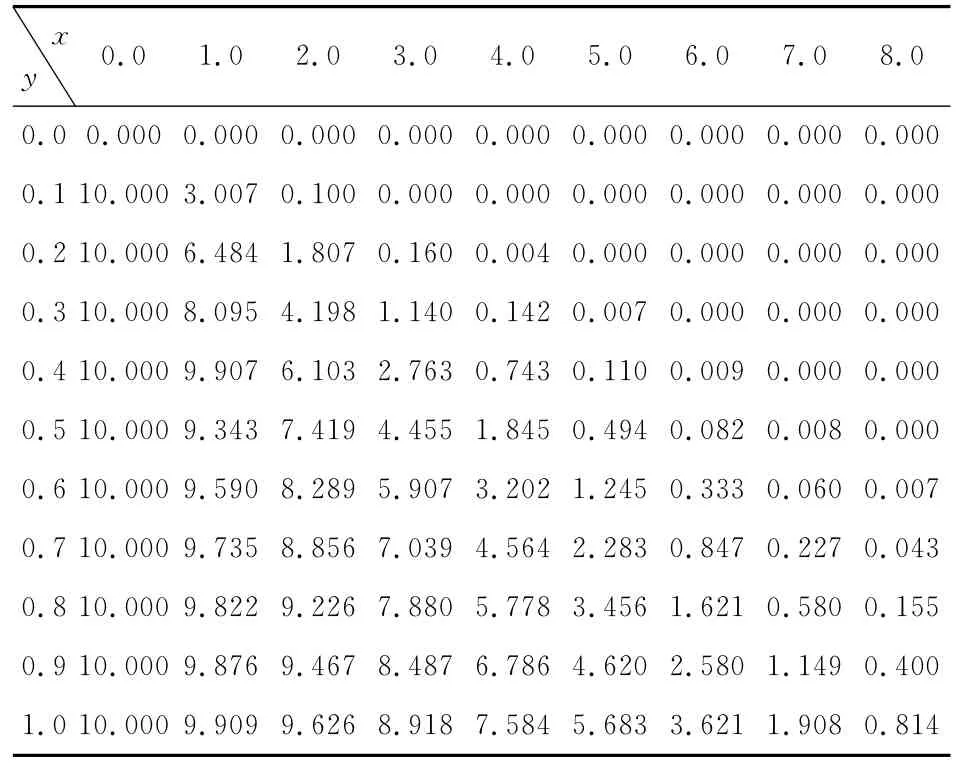
表1 污染物在各点的浓度

4 结果分析

由于差分格式（4）可改写为

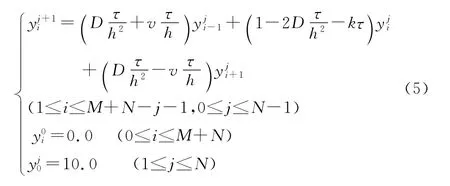
可以证明［11］：当

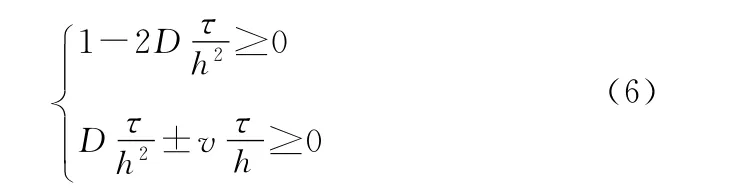
时，差分格式（4）是数值稳定的，且以O（τ＋h2）阶收敛。

容易验证：在差分格式（4）中，所取步长及常数是满足式（6）的，即按差分格式式（4）进行计算，所得结果表1是切合实际的。

5 结语

本文利用所建立的水质模型，对一段长8km河流的某种污染物浓度进行现状模拟，结果表明，计算值与实测值比较接近，模型可以接受。此外，通过本模型可以计算出污染物允许的最大排污量，为科学预测河流污染物提供可靠的理论依据，这样才有可能还河流的清白、纯净，才能可持续利用河流资源为人类子孙后代的生存提供良好的保障。由此可见，对河流水质数学模型的研究，为河流水质的控制与流域规划等都有重要的应用价值。

［1］郭劲松，李胜海，龙腾锐.水质模型及其应用研究进展［J］.重庆建筑大学学报，2002，24（02）：109－115.

［2］王焕.水污染问题特征有限差分方法的数值计算及理论分析［J］.山东大学学报（理学版），2003，38（03）：53－60.

［3］王玲杰，孙世群，田丰.河流水质模拟问题的探讨［J］.合肥工业大学学报（自然科学版），2005，28（03）：260－265.

［4］张国坤，李恒达.河流水质模型的分析及研究意义［J］.吉林师范大学学报（自然科学版），2004，26（03）：68－70.

［5］汪家权，陈众，武君.河流水质模型及其发展趋势［J］.安徽师范大学学报（自然科学版），2004，27（03）：242－245.

［6］吴迪军，黄全义，孙海燕，等.突发性水污染扩散模型及其在GIS平台中的可视化［J］.武汉大学学报（信息科学版），2009，34（02）：131－134.

［7］Kazmi A A，Hansen I S.Numerical Models in Water Quality Management：A Case Study for the Yamuna River［J］.Water Science Technology，1997，36：193－200.

［8］孙志忠，袁慰平，闻震初.数值分析［M］.南京：东南大学出版社，2002：267－287.

［9］苏煜城，吴启光.偏微分方程数值解法［M］.北京：气象出版社，1989.

［10］姜启源，谢金星，叶俊.数学模型［M］.北京：高等教育出版社，2003.

［11］宋辉，周晶，邹文萌.基于HLA的水面舰艇作战仿真系统研究［J］.计算机与数字工程，2011（9）.

［12］钱云，张寿东.水污染事件应急响应联动系统设计与实现［J］.计算机与数字工程，2008（3）.

［13］李荣华.偏微分方程数值解法［M］.北京：高等教育出版社，2005：201－288.

［14］Thomas J W.Numerical Partial Differential Equations［M］：Finite Difference Methods.New York：Springer－Verlag，1995.