飞轮姿控微小卫星控制方法研究＊

李华山 闫 野 任 利

（1.防空兵学院 郑州 450052）（2.国防科技大学航天与材料工程学院 长沙 410073）

1 引言

随着航天技术的发展，对小卫星姿态控制系统的稳态精度和响应速度要求越来越高，且对控制算法的复杂度、抗干扰性及鲁棒性有特殊要求［1］。传统控制方法是先将姿态动力学方程简化成俯仰通道和偏航－滚动通道，对前者单独控制，对后者进行解耦控制。目前，对航天器姿态控制方法多采用“优化方法＋PID控制器”组合的形式，通过优化方法整定控制器参数［2～5］，文献［6］使用 Matlab中的非线性控制设计模块实现对PD姿态控制器的参数优化，文献［7～8］分别使用遗传算法和神经元算法实现PID控制器参数调整。以上方法虽能实现对航天器姿态的精确控制，但方法较复杂，且不易满足星载小型计算机实时处理的要求。本文不考虑采用优化方法，以反作用飞轮作为控制机构，基于改进的PD控制器，对姿态耦合系统控制方法展开研究。

2 动力学方程

设沿星体的三惯量主轴各安装一个反作用飞轮，三飞轮的质心重合于星体质心。小卫星的运行轨道为低轨近圆轨道，不考虑太阳帆板扰动，由动量矩定理得到小卫星的姿态动力学方程为

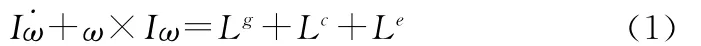
式中：I为星体的总惯量张量，且I＝diag［IxIyIz］；ω为星体角速度；Lg，Lc，Le分别为引力梯度力矩、飞轮转轴上电机的控制力矩和外力矩。

考虑到引力梯度矩Lg的表示式为

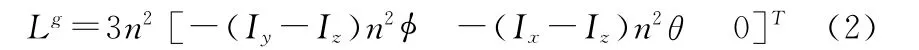
联立式（1）、（2），进行线性化得

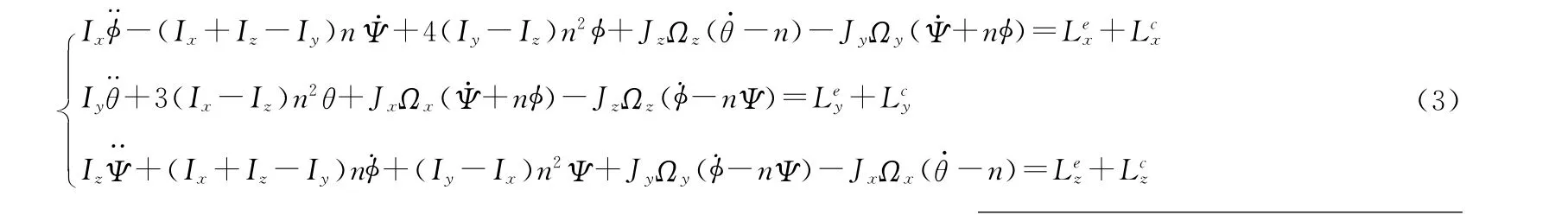
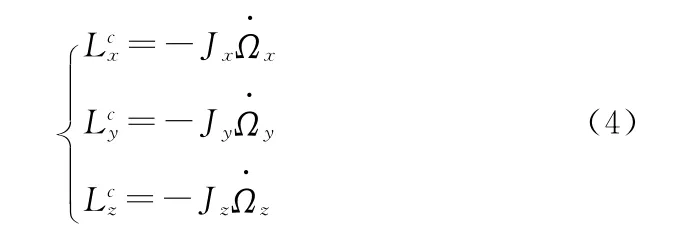
式中：φ，θ，Ψ分别为星体的滚动角、俯仰角与偏航角；n为卫星沿轨道转动角速度；Ωx，Ωy，Ωz为飞轮相对于星体的角速度；Jx，Jy，Jz分别为三飞轮的轴向转动惯量［9］。

由以上可得，卫星的姿态动力学方程是一个三输入三输出系统，且姿态的俯仰、偏航和滚动三通道相互耦合。通过解耦实现对卫星姿态的控制比较复杂，且不能满足星载计算机实时处理的要求。

3 控制器设计

3.1 PD控制器及改进

PD控制器具有原理简单，使用方便，适应性强，鲁棒性强等优点，是一种普遍的控制规律［11］。基本的PD控制规律可描述为

式中：Kp为比例系数，Kd为微分系数，两者都是可调的参数。增大比例系数，系统的响应速度加快，系统的超调也增加，调节时间也增长；增大微分时间常数，系统的超调量减小，稳定性提高，上升时间减小，快速性提高。

控制器参数整定多采用现代优化算法，计算过程复杂，效率低，通过设计的期望目标函数代替星体姿态角及角速度目标值的方法，可实现稳定控制器输入量，增强控制器参数的适用性，避开参数优化过程。期望目标姿态角函数的设置基于初始姿态角、目标姿态角和期望姿态调整时间三个因素建立。以俯仰角θ为例，期望目标函数设置为

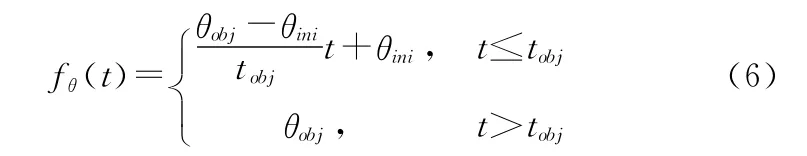
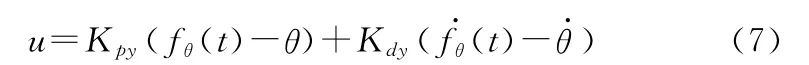
式中：θini为星体初始俯仰角，θobj为星体俯仰角目标值，tobj为期望调整时间。改进后的俯仰通道控制律描述为式中：Kpy为俯仰通道比例系数，Kdy为俯仰通道微分系数，fθ（t）、（t）分别为俯仰角及角速度的目标函数，u为控制器输出量。图1所示为改进的PD控制器结构图。

3.2 姿控系统结构

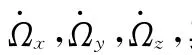
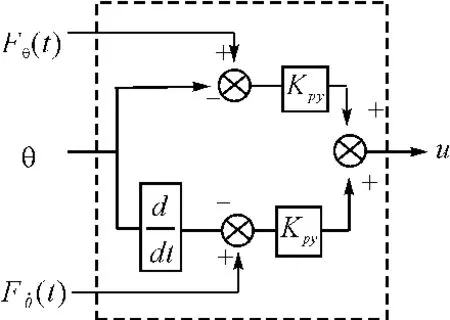
图1 改进的PD控制器结构

4 仿真分析

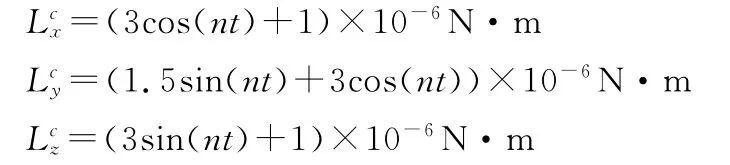
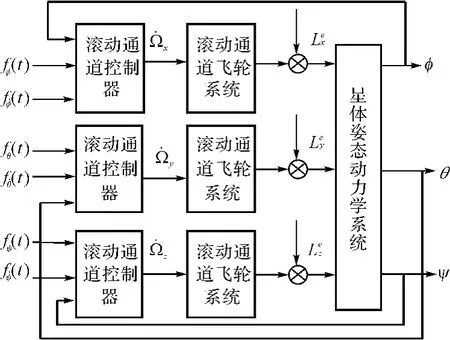
图2 控制系统结构图

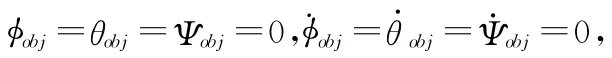
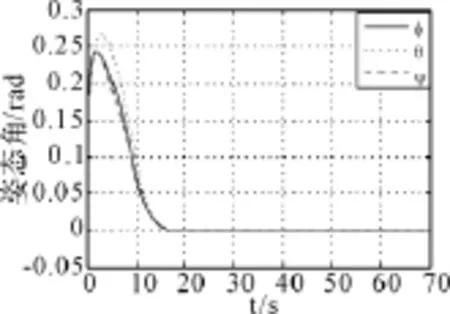
图3 姿态角响应

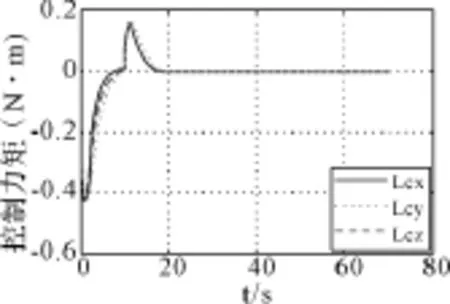
图4 控制力矩

在实际空间环境中，干扰力矩无法精确预知，其幅值可能在可在一定范围内波动。将干扰幅值提高一个量级，即时，其姿态角的响应如图5所示。与图3相比，其响应过程变化微小，系统稳态精度保持不变，控制效果明显。

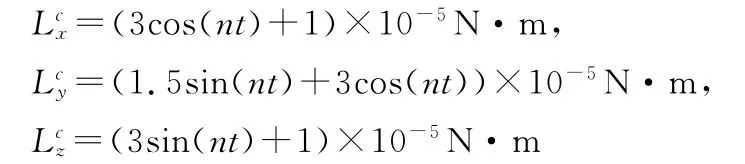
考虑飞轮系统电机性能等影响，认为飞轮实际输出的控制力矩是理想控制力矩的85%，即

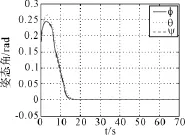
图5 干扰变化后的姿态角响应

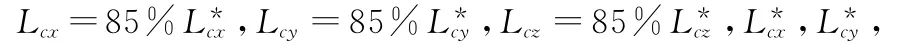
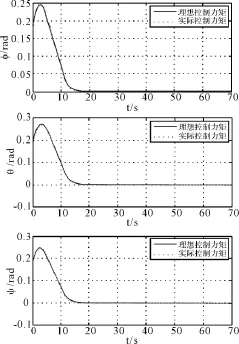
图6 实际控制力矩下的姿态角响应

5 结语

本文通过设计期望目标函数的方法，将姿态角及角速度目标值设置为期望目标函数的形式，其与实际姿态角及角速度的偏差作为控制器的输入、飞轮转动角加速度作为输出，不考虑解耦控制，在每个通道分别加入控制器。仿真结果证明：控制系统在保证姿态响应过程有良好的快速性及较高的稳态精度基础上，且对环境干扰变化及星体内部不确定性具有良好的适应性。在实际应用中可直接通过星载计算机生成期望目标函数，简单高效。稳态响应时间与理想调整时间有一定延迟，但满足工程指标。

［1］刘昆，刘述田，等.微小卫星反作用飞轮控制方法研究［J］.上海航天，2004，21（2）：11－13.

［2］王伟，张晶涛，柴天佑.PID参数先进整定方法综述［J］.自动化学报，2000，26（3）：347－355.

［3］Astrom K J，Hagglund T，Wallenborg A.Automatic Tuning of digital Controllers with applications to HVAC plants［J］.Automation，1993，29（5）：1333－1343.

［4］Astrom K J，Hagglund T，Hang C C，Ho W K.Automatic Tuning and adaptation for PID Controllers－A survey ［J］.Control Eng.Pratice，1993，1（4）：699－714.

［5］Schei T S.Automatic tuning of PID controllers based on transfer function estimation［J］.Automatica，1994，30（12）：1983－1989.

［6］周黎妮，唐国金.基于Matlab／Simulink的航天器姿态动力学与控制仿真框架［J］.系统仿真学报，2005，17（10）：2517－2520.

［7］李源，吴宏悦.基于遗传算法PID整定的卫星姿态控制研究［J］.中国空间科学技术，2007（4）：66－71.

［8］刘军，韩湘.基于单神经元的卫星姿态自适应PID控制［J］.计算机仿真，2006，23（3）：45－48.

［9］黄钏圭.航天器姿态动力学［M］.长沙：国防科技大学出版社，1997.

［10］白洪瑞，吕强，刘峰，等.基于UM6惯导模块的四旋翼飞行器姿态控制［J］.计算机与数字工程，2012（8）.

［11］刘金琨.先进PID控制 Matlab仿真［M］.第二版.北京：电子工业出版社，2006.