OFDM中基于变换域DFT信道估计算法研究＊

杜永锋

（公安海警学院电子技术系 宁波 315801）

1 引言

正交频分复用（OFDM）技术可把频率选择性信道转换为多个平坦子信道，并利用循环前缀来避免符号间干扰，使得信道均衡变得非常简单，目前已经广泛应用于众多的高速数据传输领域［1～2］。

OFDM系统一般采用相干检测方法进行解码，这就要求获得准确的信道状态信息（CSI）。研究表明，利用梳状插入的导频方式可以对时变信道环境进行可靠的估计。其中导频信道估计可采用最小平方法（LS）、最小均方误差法（MMSE）等方法［3～4］，LS估计性能虽不如 MMSE，但其计算复杂度较低。如何在LS信道估计的基础上，尽量提高估计性能，人们提出了基于离散傅立叶变换（DFT）的变换域信道估计算法［5～6］。在实际系统中，由于采样间隔是系统参数，而信道多径时延是随机变量，所以存在非整数倍采样间隔的多径时延。此时采用DFT方法时，能量并不会像整数倍采样间隔多径信道那样集中，会出现能量泄露，影响系统性能。

本文对传统的基于DFT变换域插值的信道估计方法进行了改进。首先根据LS算法得到梳状导频处的信道估计值，然后利用IDFT变换到时域，将较弱能量点置零，再适当选取补零的位置后变换到频域得到所有子载波处的信道估计。该算法有效地减小了非整数倍采样间隔多径时延能量扩散的影响，增强了算法对多径延迟分布的鲁棒性，有效提高了系统的性能。

2 系统模型

假设OFDM系统子载波总数为N，利用矩阵的表示形式，OFDM系统可表示为

式中Y为N×1的接收信号向量；X为N×N对角矩阵，对角线上的元素即为传送的导频和数据信号；W 为一独立同分布的高斯噪声向量；H为信道的频域响应向量，其时域信道冲激响应（CIR）可以表示为

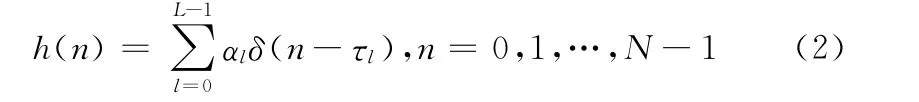
其中L为信道的多径数，αl和τl分别为第l条路径的信道增益和时延。

假设信道冲激响应长度不超过循环前缀长度，则信道频域响应（CFR）可表示为

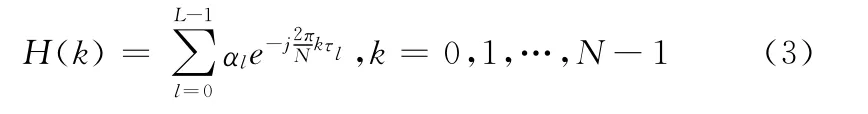
3 变换域信道估计

3.1 不同采样间隔信道时延特性分析

对式（3）抽样，则得到离散的信道冲激响应为

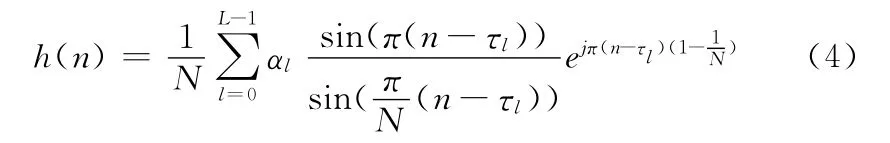
由式（4）可知，当n－τl为整数时，h（n）仅在n＝τl时有值，在n－τl为其它整数时值都为0。因此，当路径延迟τl为采样间隔的整数倍时，该路径的所有能量将映射到抽头h（τl）上。当τl为非整数时，h（n）在所有n处都有值，也就是说非整数倍采样间隔延迟使得路径能量扩散到所有抽头上，不过大部分能量还是集中在临近的若干抽头上。图1为h（t）＝δ（t－0.5T）＋δ（t－4.5T）＋δ（t－10.2T）以及每一径都为整数偏移时的信道冲激响应曲线。

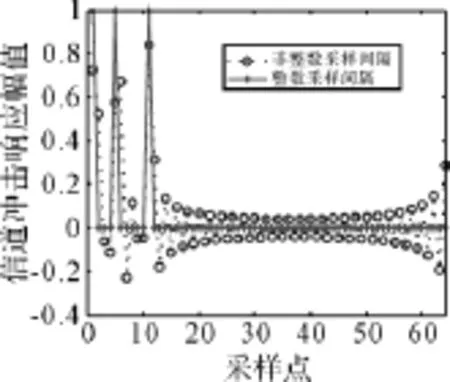
图1 不同采样间隔对应的信道冲激响应幅值

3.2 基于DFT的信道估计

假设一个OFDM符号中导频位置上的信道响应为Hp＝［Hp（0），Hp（1），…，Hp（Np－1）］，则有：

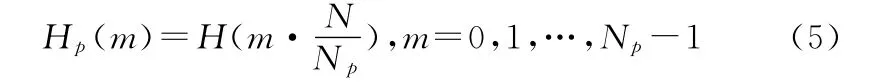
对Hp采用Np点IDFT操作，得到CIR的估计序列为

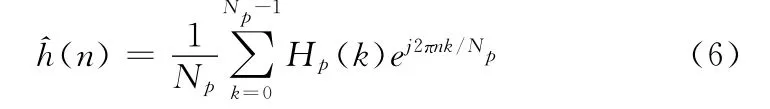
将式（5）代入式（6）得：

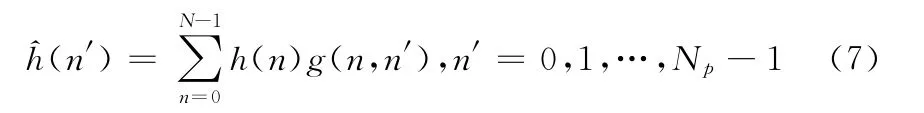
为了得到所有子载波处的信道响应，我们必须对Np个导频点信道响应值进行变换域补零操作，根据补零位置的不同，有不同的算法出现［7～9］。

1）尾部位置补零

在整数倍采样间隔信道延迟条件下，当Np不小于最大路径延迟时，由式（4）和（7）可得：

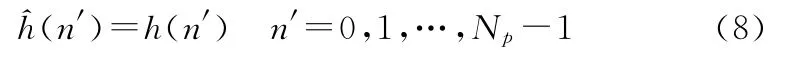
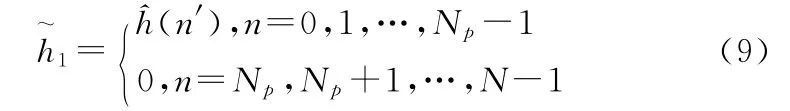
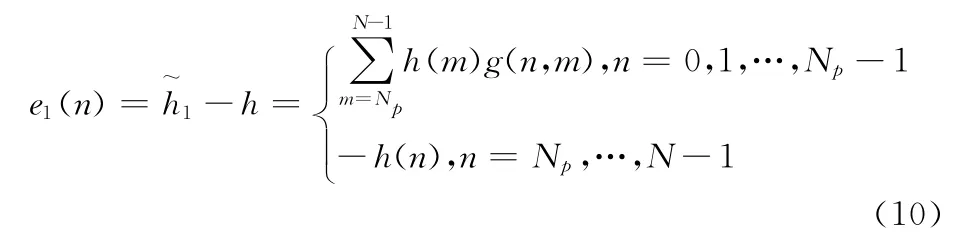
2）中间位置补零

在非整数倍采样间隔信道延迟情况下，存在能量泄露，即使不存在噪声，式（8）也不再成立。此时采用在h＾中间位置补零，得到的序列为

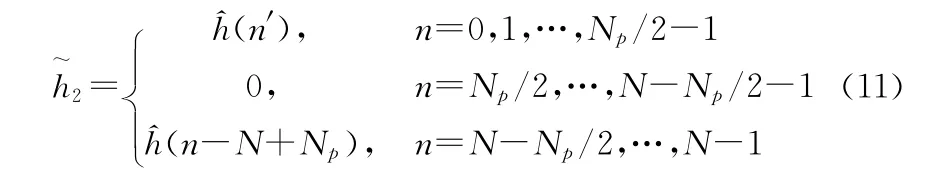
此时对应的估计误差为

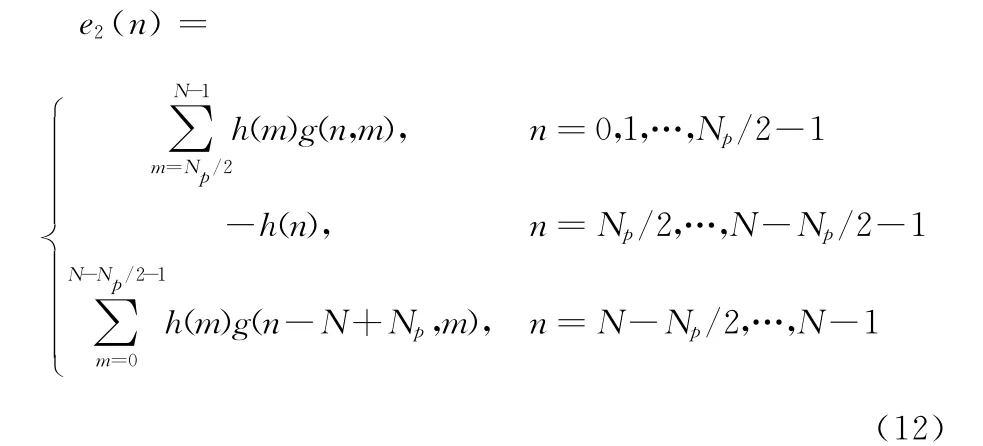
3.3 改进的基于DFT的信道估计方法

根据前面的分析可知，对估计序列进行补零的操作实际上是对N点CIR采样序列的一种逼近或重构。重构误差大小将直接影响信道估计性能优劣。由式（10）和（12）可以得到如下结论：

1）在多径信道中，当存在延迟小于Np／2的非整数倍采样间隔路径时，在中间位置补零的方法将在补零区域两端引入较大的重构误差，特别是在此延迟存在于Np／2附近时，这种重构误差会更大，并且对应的路径复增益越大，重构误差也就越大。

2）当出现延迟大于 Np／2的路径时（τl＞Np／2），在τl和τl＋Np／2处存在较大的重构误差。

3）当第一径为非整数倍采样间隔路径时，序列h尾部会出现较大能量泄露，在后部补零的方法将在n＝Np和n＝N附近引入较大的重构误差。

由上面的分析可知，为减少补零引入的误差，应适当选取补零的位置。综合考虑前述两种典型情况下算法的优缺点，这里提出一种折衷的补零方法，该算法在基本不增加复杂度的情况下可以有效地提高信道估计精度。

前述的两种算法的补零位置分别为Np和Np／2，我们取其中间位置开始补零。首先根据导频估计出信道冲激响应，并设定一个门限值，据此估计出信道的最大路径时延，则补零的起始位置为（记该方法为“方法1”）：

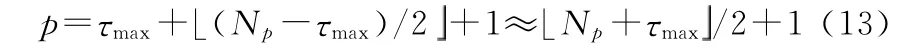
实际应用中，为了提高信道估计性能，导频数目Np通常以2倍过采样进行设置［10］。因此，一般情况下导频数目Np都大于保护间隔的长度Ng。另外，为了保证上一个符号的多径分量不会对下一个符号产生干扰，一般选择Ng＞τmax，因此在实际应用中可采用更为简单的补零位置设置方法（记该方法为“方法2”）：

可以看出，“方法1”比“方法2”所确定的补零起始位置更确切，更贴合实际信道条件，当然是以增大计算复杂度为代价的，并且与所设定的门限值关系重大。具体的性能差异情况将在下一节的仿真分析中给出，这里不再赘述。

图2给出了不同非整数倍采样间隔延迟路径条件下，不同补零方法得到的重构误差，其中N＝64，Ng＝16，梳状导频子载波数Np＝32。由于两种改进的补零方法差异不是很大，在图中难以区别显示，这里只给出其中的一种。假设系统已经理想同步，并且不考虑白噪声的影响。可以看到，改进的补零方法所得到的重构误差最小。

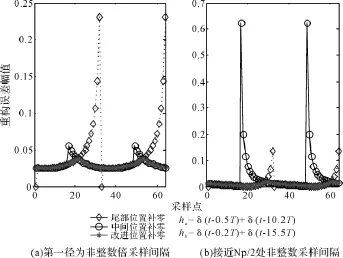
图2 采用三种不同补零方式对应的重构误差

4 算法性能仿真及讨论

为了进一步验证上述分析的正确性和改进方法的有效性，本节对所提的信道估计方法进行仿真。仿真中的信息比特通过（2，1，7）卷积码进行编码并利用QPSK调制，N＝1024，Ng＝128，Np＝256，一帧信号包含十个数据 OFDM符号。在三种不同采样间隔的等幅多径信道条件下仿真：1）h1（t）＝δ（t－0.5T）＋δ（t－100.2T）；2）h2（t）＝δ（t－0.1T）＋δ（t－100.1T）；3）h3（t）＝δ（t）＋δ（t－100T），可以看到，信道1的两径存在较大的非整数倍采样间隔延迟，也就是说存在很大的重构误差；信道2的非整倍采样间隔比较小且两径延迟一致，所以信道条件要好些，重构误差较小；信道3为整数倍采样间隔延迟的情况，也就是理想上是不存在重构误差的。为了便于比较和讨论具有针对性，假定系统已经理想同步。仿真中还给出了不同频域内插的效果。

图3给出了在信道1条件下，不同内插信道估计方法和补零DFT方法的误码率性能。可以看到，在三种内插的方法中，基于线性内插的平层最高，二阶内插的性能次之，三次样条内插的平层最低。另外，基于内插的信道估计方法比补零DFT方法的性能要差，这是显而易见的，基于内插的方法主要是根据邻近几个导频信息进行内插估计，而变换域方法利用所有导频信息通过补零、IDFT运算实现高分辨率插值。

从前面的分析可知，0.5T的非整数倍偏移构成的重构误差是最大的，所以在信道1条件下，尾部位置补零的性能要比中间位置补零的性能差。改进的两种方法最好，但差异并不是很大，这是因为即使存在非整数倍采样间隔路径，采用两种方法确定出的位置上能量泄漏均较微弱。虽然改进方法2比方法1性能上稍微差一点点，但是由于不需要进行额外的门限设置，最大时延等运算，所以更为简便和实用。基于此，后续的仿真图中也只给出改进方法2的结果。

需要特别说明的是，在考虑抑制噪声的情况下（也即先将较弱能量点置零，再利用补零的方法），当SNR小于18dB左右时，该方法的性能在所有方法中最佳，但是随着信噪比的增高，其性能明显下降。这是因为系统中存在高斯白噪声的同时，还存在非整数倍采样间隔延迟引起的重构误差，在信噪比较小时，高斯白噪声为主导干扰因素，所以将较弱能量点置零起到了抑制白噪声干扰的效果，但随着信噪比的增高，降噪的好处将小于多径泄露能量的损失，使得性能得不到改善。从图4也可以得到此结论。由于两径都引起重构误差，所以采用尾部和中间位置补零的方法都只能消除部分的重构误差，这就造成图3～图4中，当SNR大于20dB时，出现了误差地板效应。而改进方法能同时有效减小多种重构误差，增强改进算法对信道路径延迟分布的鲁棒性，有效提高了系统性能。

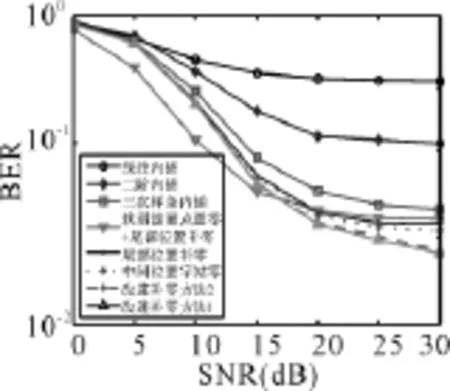
图3 信道1条件下，不同信道估计方法的误码率性能

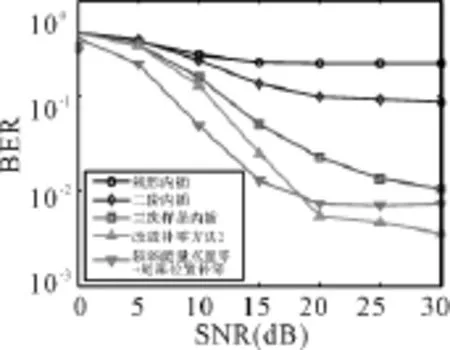
图4 信道2条件下，不同信道估计方法的误码率性能

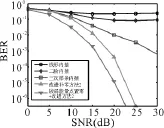
图5 信道3条件下，不同信道估计方法的误码率性能

图5给出了信道3条件下，不同信道估计方法的误码率和均方误差性能。由于没有重构误差的影响，各种方法的性能都很好，且如前所述，这种信道条件下，基于较弱能量点置零的方法是最优的。

5 结语

本文研究了梳状导频模式下的OFDM信道估计方法，针对非整数倍采样间隔信道时延会造成能量扩散到所有信道抽头点上的问题，本文提出了基于变换域补零DFT的信道估计方法，并与经典的频域多阶插值算法及两种不同的补零DFT算法进行了详细的性能比较。仿真结果显示，改进的方法增强了算法对多径延迟分布的鲁棒性，具有较低的复杂度和较好的性能。

［1］Floch B L，Halbert－Lasalle R，Castellain D.Digital audio broadcasting to mobile receivers［J］.IEEE Trans.Consum.Electron.，1989，35（3）：493－503.

［2］Stuber G，Barry J，Mclaughlin S，et al.Broadband MIMO OFDM wireless communications［J］.Proc.IEEE，2004，92（2）：271－294.

［3］Speth M，Fechtel S A，Fock G，et al.Optimum receiver design for wireless broad－band systems using OFDM－Part I［J］.IEEE Trans.Commun.，1999，47（11）：1668－1677.

［4］Jeon W G，Paik K H，Cho Y S.Two－dimensional MMSE channel estimation for OFDM systems with transmitter diversity［C］／／Proceedings of the VTC 2001，Atlantic City，USA，Oct.，2001：1 682－1 685.

［5］Jeong－Wook Seo，Jung－Wook Wee，Won－Gi Jeon，Jong－Ho－Paik and Dong－Ku Kim.An Enhanced DFT－Based Channel Estimation Using Virtual Interpolation with Guard Bands Prediction for OFDM［C］.IEEE Personal，Indoor and Mobile Radio Communications（PIMRC’06），2006：1－5.

［6］Li Huang，G.Mathew and J.W.M.Bergmans.Pilot－Aided Channel Estimation for Systems with Virtual Carriers［C］.IEEE International Conference on Communications（ICC’06），2006.vol.7，pp.3070－3075.

［7］An C，Jang S，Lee J，et al.DFT－based Channel Estimation U－sing CIR Adaptation in OFDM Systems［C］／／ICACT，2007，1：23－26.

［8］Kwak K，Lee S，Kim J，et al.A New DFT－based Channel Estimation Approach for OFDM with Virtual Subcarriers by Leakage Estimation［J］.IEEE Transactions on Wireless Communications，2008，7（6）：2004－2008.

［9］Zheng K，Su J，Wang W.DFT－based Channel Estimation in Comb－type Pilot－aided OFDM Systems with Virtual Carriers［C］／／IEEE PIMRC，2007：1－5.

［10］Yang B，Cao Z，Letaief K B.Analysis of Low－complexity Windowed DFT－based MMSE Channel Estimator for OFDM Systems［J］.IEEE Transactions on Communications，2001，49（11）：1977－1987.