基于OFDM的宽带短波波形信道估计算法研究＊

李晓勇 李丁山

（武汉船舶通信研究所 武汉 430079）

1 引言

OFDM是一种特殊的多载波调制技术，与传统多载波调制技术相比，有许多优点：把整个宽带传输带宽分成很多个窄带子载波，在一定程度上能抵抗宽带短波信道的频率选择性衰落；引入了循环前缀，能减少符号间干扰；各子载波间是正交关系，载波间频谱互相重叠，提高了频谱利用率［1］。正因如此，OFDM已被列入4G无线通信系统的解决方案，受到研究者的广泛关注。

在宽带短波传输中，多径衰落和信道的时变性是不可避免的存在，对应于信道的频率选择性和时间选择性。特别是短时间内的频率选择性，会对系统造成比较大的性能损失。如果接收方知道信道的衰落情况，就能对衰落频点进行补偿，从而恢复出正确的信号。所以，信道响应进行实时的估计对正确恢复出传输的数据就显得十分重要。文献［1］利用了维纳滤波器的方法来进行信道响应的估计，但维纳滤波需要预先知道信道特性，这在实际应用中很难做到。本文着重研究了短波信道信道响应的估计问题，经过仿真分析，找到了一种比较适合短波信道的信道响应估计方法。

2 OFDM系统的组成及工作原理

2.1 系统组成

OFDM系统的组成如图1所示：该系统主要分为四部分：第一部分为发射端基带处理单元（包括编码，交织，数字调制，串并变换等模块）；第二部分为发射端射频单元（包括DAC，射频模块）；第三部分为接收端射频单元；第四部分为接收端基带处理单元（包括同步，信道估计与补偿，解调及解码等模块）。

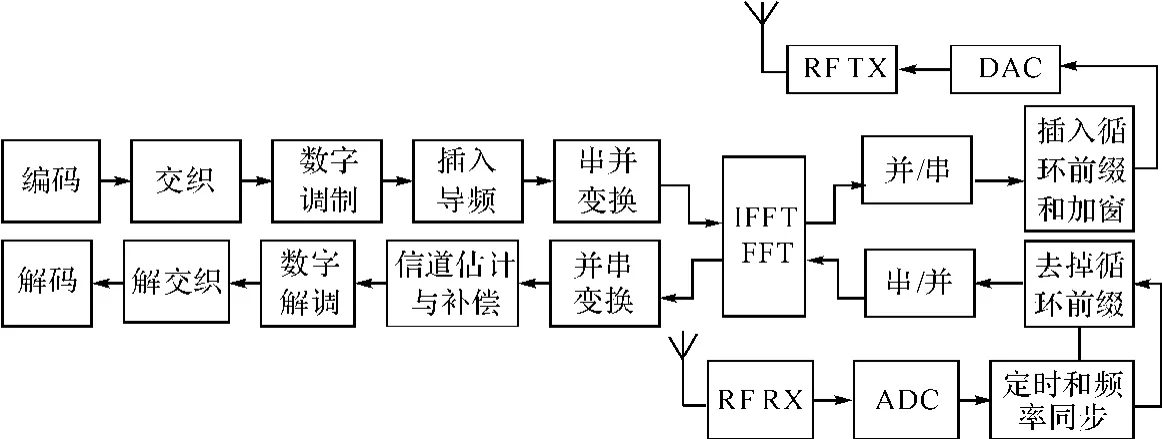
图1 OFDM系统组成框图

2.2 OFDM系统工作原理

正交频分复用（OFDM）是多载波调制技术的一种。多载波调制的基本思想是把数据流串并变换为N路数据较低的子数据流，用它们分别去调制N路子载波后再进行并行传输。

我们希望这种多载波传输方式的频谱利用率要高，即子载波间隔要尽可能小；还希望系统实现要简单。

如果子载波间隔设为Δf＝1／Tu，Tu为有用信号长度，那么可以用DFT的快速算法FFT来实现这个多载波并行调制的过程。OFDM系统工作原理如图2所示。

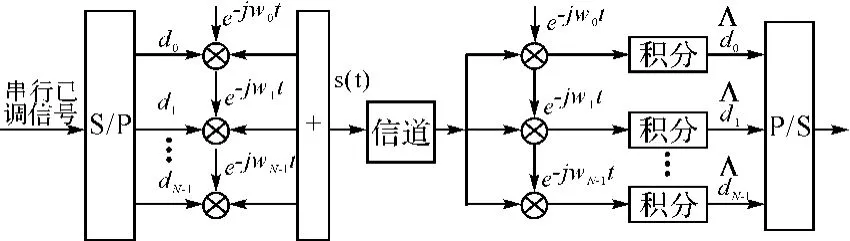
图2 OFDM系统工作原理框图

3 OFDM系统信道估计算法

信道估计方法分为盲估计和基于导频信号估计方法；依据不同的导频插入方法可分为梳状导频估计方法，块状导频估计方法和二维导频估计方法。由于短波信道的时变特性，我们采用对时变不是很敏感的梳状导频估计方法，处理过程为：

1）在发送端的适当位置插入所选择的导频单元；2）在接收端利用导频恢复出导频位置的信道响应。

导频载波处的信道增益估计方法一般有两种：一种是简单的最小二乘算法，它计算简单，容易实现，实用性比较广；另一种是最小均方误差算法，它的特点是在均方误差意义上是最优的，但是计算量大，并且需要知道信道的先验知识，或者通过估计得到信道的统计信息。

3）通过导频位置获取的信道信息生成非导频子载波信道的信道响应。

我们一般用插值算法来根据导频子载波的信道信息来得到数据子载波的信道响应。插值方法分为线性插值［4］和变换域插值。

3.1 线性插值算法［5］

线性插值算法的原理是利用相邻导频子载波的频率响应通过线性插值算法来计算出数据子载波处的信道响应。这种算法计算量小，易于实现，但估计性能较低。该算法可表示如下：

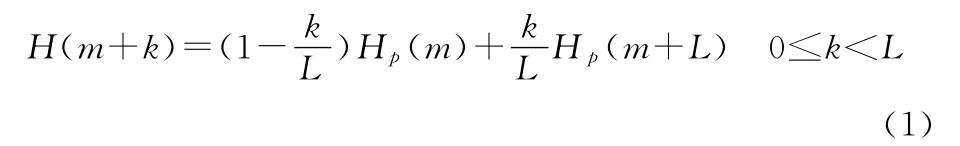
其中，Hp（m）和Hp（m＋L）为导频子载波处的信道响应，H（m＋k）为两个导频符号之间的数据子载波出的信道响应。

3.2 变换域内插算法［3～6］

由信号处理知识我们知道，频域内插等效于时域补零。因此，由导频子载波的信道响应估计出数据子载波的信道响应的过程，可以使用在导频子载波的信道冲击函数后补零，然后再把补零后的时域序列转化为频域信号的过程实现，该过程称为变换域内插算法。变换域内插算法原理如图3所示。

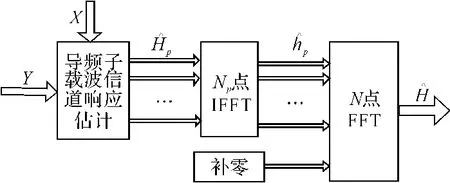
图3 变换域内插算法

这种变换域方法在高斯信道下可以很好地工作，估计性能优于线性插值算法。但是抵抗多径衰落的能力较差，在多径信道下误差底板效应明显。图6的仿真曲线也证明了这点。

3.3 一种改进的变换域方法

3.2 节中的变换域方法等效于用一个“低通滤波器”对导频信道的冲击响应进行处理，即在导频信道的冲击响应的尾部补零。对导频信道频率响应的变换域进行研究，观察导频信道频率响应的“变换域响应”，发现能量集中在原点和原点附近的“低频”区域，而噪声分布在整个“频域”中。理想导频信道频域响应的变换域特性如图4所示。

为了进一步降低噪声对信道估计的影响，可以将低通滤波器改为带阻滤波器。带阻滤波器算法与上节中的低通滤波器算法的区别主要为低通滤波器是在导频信道的冲击响应的尾部补零，而带阻滤波器算法在导频信道的冲击响应的中间补零［4］。具体可由下式实现：

图4 理想导频信道频域响应的变换域特性

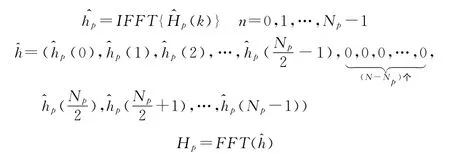
这种改进的方法能够较好地抵抗信道的多径扩展，在多径信道下也有比较理想的性能。

4 仿真分析

本文仿真使用虚拟子载波方法，具体的OFDM系统参数如表1所示。

利用上述系统参数，分别在两种信道条件下进行了仿真，高斯信道和瑞利信道。瑞利信道包含了三条路径，具体路径参数如表2所示。

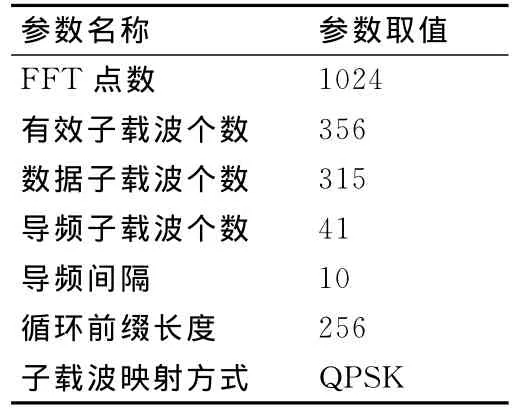
表1 OFDM系统参数

图5 高斯信道下信道估计算法仿真比较

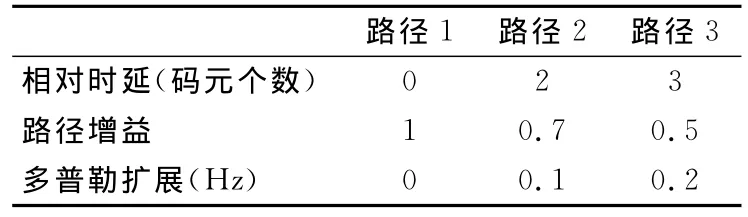
表2 瑞利信道参数

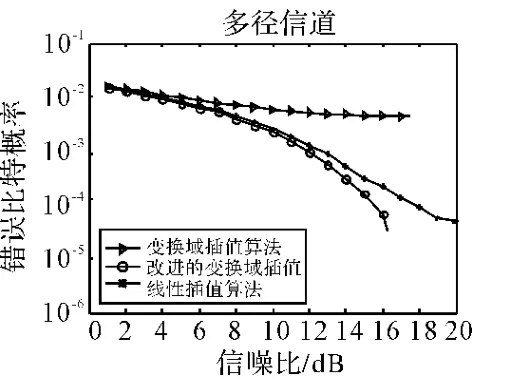
图6 多径信道下信道估计仿真比较

图5在高斯信道下对线性插值算法、变换域插值算法和改进的变换域插值算法进行了比较，总体来说，改进的变换域算法效果最好，线性插值算法和变换域插值算法性能接近。

图6在多径信道下比较了以上三种信道估计算法，可以看出，变换域插值算法效果最差，有很明显的误码率底板效应。线性插值算法和改进的变换域插值算法在低信噪比下效果相当，但当信噪比较高时（大于10dB），变换域插值性能比线性插值算法性能提高了2～4dB。

5 结语

本文在Matlab仿真平台下仿真了三种信道估计算法。结果表明，高斯信道下，变换域插值算法和线性插值算法效果接近，改进的变换域算法与这两种方法相比，性能提高了不到1dB。但在典型的短波信道下，变换域算法有明显的性能底板效应，线性插值算法性能居中，而改进的变换域算法比线性插值算法性能提高了2～4dB。所以，在实际无线信道的高速数据传输系统中，使用这种改进的变换域算法进行信道估计效果更好。

［1］Dong Li，Feng Guo，Guosong Li，et al.Enhanced DFT Interpolation－based Channel Estimation for OFDM Systems with Virtual Subcarriers［C］／／Proc.IEEE VTC＇06－Spring，Melbourne，Australia，2006，5：1580－1584.

［2］尹长川，罗涛，等.多载波宽带无线通信技术［M］.北京：北京邮电大学出版社，2004.

［3］吕春苗.OFDM宽带短波通信关键技术研究［D］.杭州：浙江大学硕士学位论文，2011，3.

［4］Yuping Zhao，Aiping Huang.A novel channel estimation method for OFDM mobile communication systems based on pilot signals and transform－domain processing［C］／／Proceedings of IEEE VTC’97.Phoenix，USA，1997，2089－2093.

［5］Huiying Jiao，Jianping An.A novel method of channel estimation for DRM system.IEEE 02［C］.2005.

［6］M.Sandell，O.Edfors.A Comparative Study of Pilot－based Channel Estimators for Wireless OFDM［C］／／Div.Signal Processing， LuleaUniv.Technology， Sweden， Res.Rep.TULEA 1996.

［7］彭明金，李智.基于叠加训练序列的MIMO－OFDM信道估计［J］.计算机与数字工程，2012（10）.

［8］汪裕民.OFDM关键技术与应用［M］.北京：机械工业出版社出版社，2006.