无人机倾斜转弯飞行控制系统设计与仿真＊

王凌艳 施敏良 林秋杰 兰 甸

（中国洛阳电子装备试验中心 洛阳 471003）

1 引言

随着无人机（UAV）开始向高空高速、大机动能力的发展，侧滑转弯（STT）控制方式已难以提供足够的过载能力来满足UAV高机动性能要求［1］。倾斜转弯（BTT）控制方式相对（STT）控制方式在气动效率、机动能力、控制性能等方面具有明显优势［2～3］，借鉴现代导弹控制系统的设计思想，BTT控制方式可以解决UAV侧向过载能力不足的问题，满足吸气式动力装置对小侧滑角的要求，是提高UAV机动性能的一项关键技术。

无人机既具有导弹的特点又有人驾驶飞机的特点，它采用面对称的飞机平台，其气动外形上的不对称性，以及BTT控制方式决定了它是一个具有较强运动学耦合、惯性耦合、气动耦合和控制耦合的多变量非线性系统［4］。为了提高无人机的制导控制精度，在BTT控制律设计中必须对模型的非线性耦合给予考虑。BTT控制系统设计面临的技术难点包括：1）由于UAV大包线飞行引起UAV参数大范围急剧变化，要求控制系统有强鲁棒性以保证UAV在整个飞行过程中始终具有优良的静态品质和动态特性，从而保持其跟踪性能在整个飞行包线范围内均能满足要求［5］；2）采用BTT控制方式的 UAV是具有气动耦合、运动耦合和控制耦合的强耦合系统［6～7］，耦合作用给控制系统设计带来了很大的挑战。

针对倾斜转弯（BTT）UAV控制中的多变量强耦合问题，文章研究了一种适用于倾斜转弯控制UAV的自适应神经网络反演算法，以实现自动驾驶仪的解耦控制。根据BTT控制的基本特性，建立UAV的非线性控制模型，并将其转化为适合于反演设计的块控模型。在此模型上，基于反演的非线性控制系统综合设计方法，并加入神经网络来估计不确定性，设计了自动驾驶仪控制器。

2 自适应反演控制律设计

控制律设计的目的是保证UAV的稳定，并达到跟踪系统侧向和法向指令信号的目的，此外在跟踪过程中还需要保持侧滑角为小量。本节将针对倾斜转弯UAV系统设计一种自适应反演控制律，该控制律加入在线神经网络估计不确定性，通过状态观测器观测神经网络权值，采用backstepping的递归算法，基于Lyapunov稳定性原理，控制系统跟踪期望的轨迹。

2.1 系统定义与假设

考虑具有如下形式的非线性系统：

式中：x＝［x1x2… xn］T为状态向量；u为实际输入向量；y为系统输出向量；Ωi为系统中存在的不确定性。

控制系统设计目标是得到能够跟踪期望输出信号的鲁棒跟踪控制器。通过自适应反演算法设计控制器，根据反演算法对系统形式的要求，对系统可作以下假设：

1）gi（i＝1，2，…，n）有界且可逆。

2）存在未知连续函数φi（x1，x2，…，xn），i＝1，2，…，n，使得‖Ωi‖≤φi，i＝1，2，…，n。

3）RBF神经网络可以逼近任意连续函数，不确定性Ωi可写成如下形式：

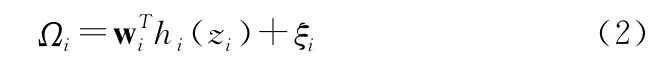
其中，

式（2）、（3）中 wi，i＝1，2…n为网络权重矩阵，为区别其他列向量与标量，使用矩阵向量形式标记；zi为输入向量；cij，j＝1，2…l为高斯函数中心点，sij，j＝1，2…l为高斯函数形状参数，l为隐含层节点数；ξi为神经网络重构误差。

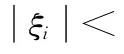
定义误差信号e1＝x1－yr，e2＝x2－x2d，…，ei＝xixid，其中yr，xid，i＝1，…，n分别为期望的输出与状态量。

2.2 反演控制器解耦设计

第1步 由e1＝x1－yr，得到

将x2作为式（4）的虚拟控制，根据反演算法，选择最优虚拟控制量

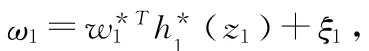
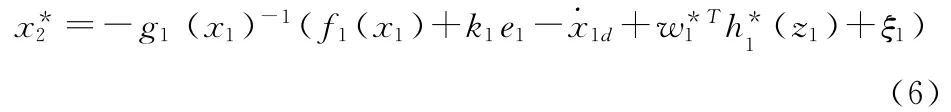
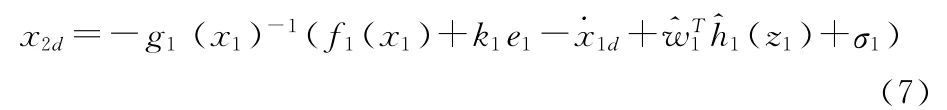
则选取Lyapunov函数如下所示

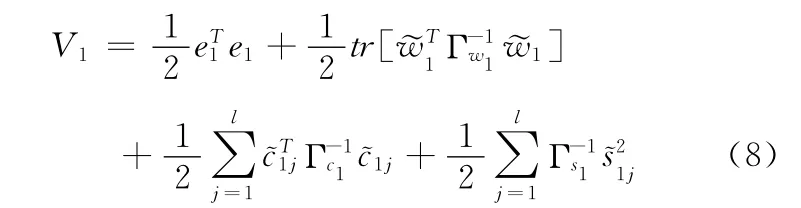
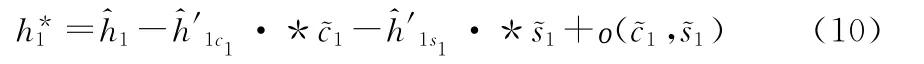
其中

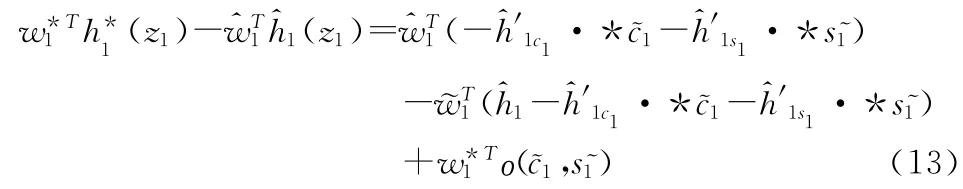
将式（10）、（13）代入式（4）得到

将式（6）、（10）、（11）、（12）、（13）代入式（4）得到

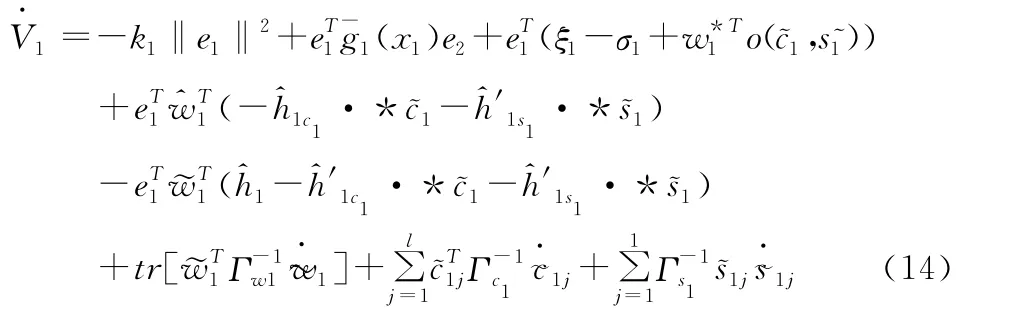
选择自适应调节律

将式（15）、（16）、（17）代入式（14），得到

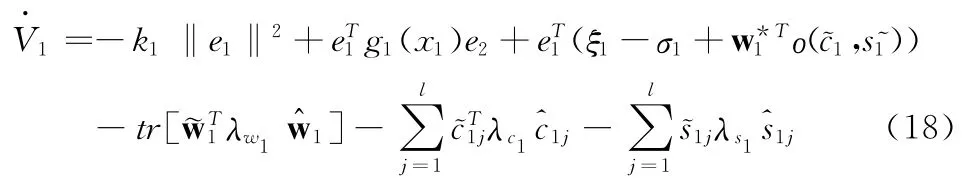
有

鲁棒项取为

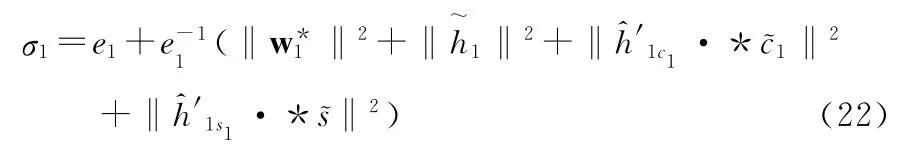
将式（19）、（20）、（21）、（22）代入式（18）

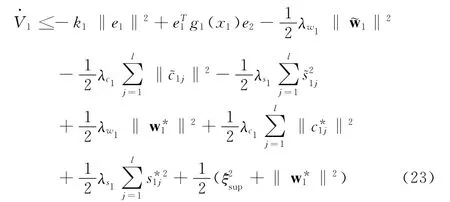
第n步 误差量en＝xn－xnd，对en求导得到

选择最优控制

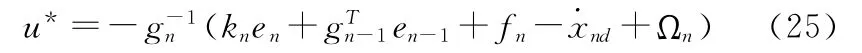
用RBF神经网络对不确定补偿，对神经网络权值和高斯函数估计得到

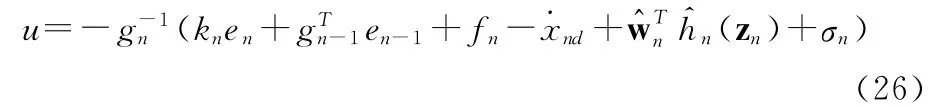
σn为引入的鲁棒项。选取Lyapunov函数

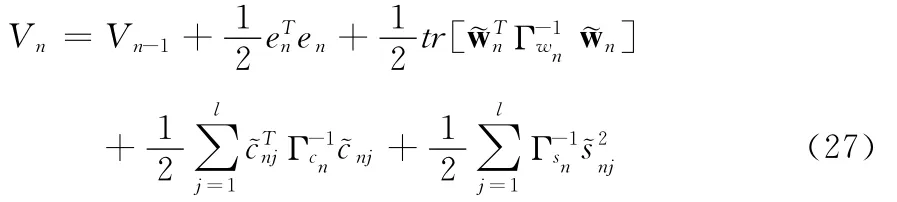
自适应调节律和鲁棒项取为

将式（28）、（29）、（30）、（31）代入式（27）得到

其中

2.3 稳定性分析

3 无人机倾斜转弯控制系统自适应反演设计

由于无人机（UAV）通常为面对称布局，因此在侧滑和滚动通道间存在与攻角密切相关的强耦合，此外滚动和偏航通道也存在较强的控制耦合。这种非轴对称的气动布局和特殊的控制方式，使得通常的线性解耦假设会导致较大的模型失真，因此需要建立考虑耦合因素的UAV非线性模型。

3.1 BTT控制UAV系统反馈模型

为了设计控制律，需要建立BTT控制UAV系统模型。在不考虑地球自转及机体气动变形的情况下，基于弹体坐标系，在文献［8］所给定气动参数的条件下，UAV飞行的动力学方程可以表示为

由此模型可以看出，在俯仰、偏航、滚转三通道存在明显的交叉耦合，是一个非线性强耦合的复杂多变量系统。tan（β）pcos（α）、psin（α）分别是俯仰，偏航通道中的运动耦合，qr、pq、pr分别为滚转、俯仰、偏航三通道间的惯性耦合。这些耦合项随滚转角速率p的增大而增大。在BTT控制无人机飞行过程中，由于滚动通道起主要控制作用，p的数值较大，因此在控制律设计过程中不能忽略由于滚动带来的控制耦合问题。

反演设计是一种基于Lyapunov方法的控制系统设计技术，能够适用于严格反馈系统或块反馈系统。为了便于利用反演设计控制律，并实现控制解耦，根据块控原理［9，11］，在不考虑地球自转及UAV机体气动变形的情况下，UAV的非线性控制模型可以改写成状态反馈块模型：

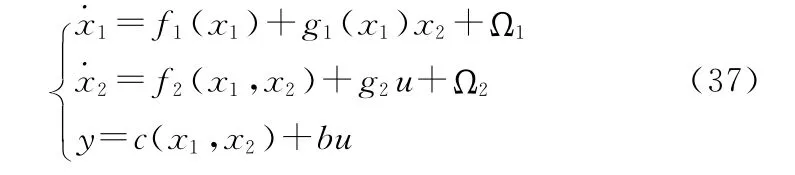
其 中，x1＝ ［αβφ］T，x2＝ ［p q r］T，u＝ ［δpδqδr］T，y＝［nynz］T。Ω1、Ω2为由于气动参数随时间变化、外部扰动、噪声引起的不确定项。

3.2 BTT控制UAV系统自适应反演设计

针对BTT控制UAV系统模型，通过神经网络自适应反演算法得到第一个虚拟控制

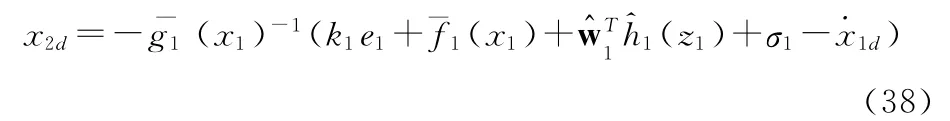
根据所推导RBF神经网络自适应反演算法取自适应调节律和鲁棒项

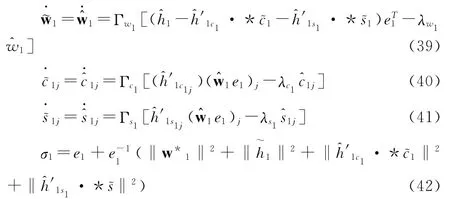
对式（37）取实际控制

自适应调节律和鲁棒项

4 仿真结果

在UAV倾斜控制系统模型上进行仿真，对于面对称布局的UAV，通常采用BTT－90控制方式，因此，倾斜控制系统调试参数时选取幅值为90°的阶跃输入作为倾斜角输入指令。

图1 指令信号为正弦波信号时跟踪曲线

选择控制器参数k1＝25，k2＝20，Γc1＝Γc2＝0.1，λw1＝λw2＝0.047，λs1＝λs2＝0.025，λc1＝λc2＝0.6。图1为指令信号为正弦信号时，在无扰动的情况下，侧滑角、攻角、侧向和法向过载跟踪指令信号曲线图。图2、3、4分别为参数摄动条件下滚转角、法向过载跟踪曲线，其中实线和点线分别为指令曲线和无参数摄动条件下跟踪曲线，点划线和虚线分别为Clδp向上和向下摄动20%时的跟踪曲线。图5为侧滑角控制图。

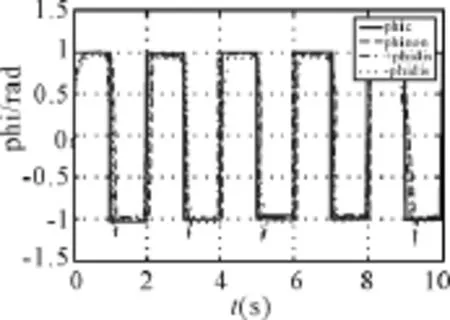
图2 参数摄动条件下滚转角跟踪曲线

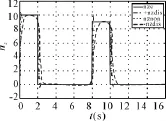
图3 指令信号为方波信号时参数摄动条件下滚转角跟踪曲线

图4 指令信号为正弦波信号时参数摄动条件下滚转角跟踪曲线

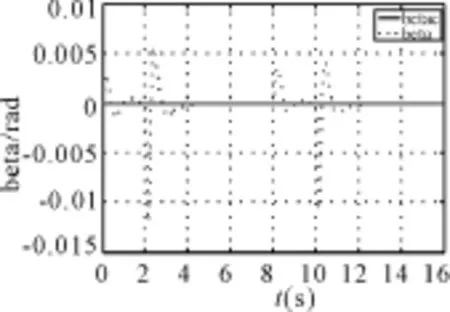
图5 指令信号为方波信号时侧滑角控制图

由图1可以看出，在不存在参数扰动的条件下，所设计的UAV飞行控制系统能够在保持侧滑角和法向过载为小量的同时较好跟踪滚转角和侧向过载指令；由图2、3、4、5可以看出所设计的系统在参数扰动条件下，仍然能够很好的跟踪滚转角和侧向过载指令，同时保持侧滑角为小量，这证明该系统具有较好的鲁棒性和自适应性。

5 结语

在建立无人机倾斜转弯控制反馈块模型的基础上，通过加入自适应神经网络的反演算法设计了无人机倾斜转弯飞行控制系统。仿真结果显示该控制器能够实现控制解耦目的，且对指令信号跟踪效果良好，表明了加入自适应反演算法设计无人机倾斜转弯飞行控制系统的可行性和有效性。

［1］李怡勇.无人机非线性飞行控制方法研究［D］.北京：装备指挥技术学院，2005：4－6.

［2］R.T.Reichert.Homing Performance Comparison of Selected Airframe Configurations Using Skid－to－Turn and Bank－to－Turn Steering Policies［R］.National Aeronautics and Space Administration，1981：723－725.

［3］Frederick W.Riedel.Bank－To－Turn Control Technology Survey for Homing Missiles［R］.National Aeronautics and Space Administration，NASA Contractor Report，1980：123－130.

［4］郑建华，杨涤.鲁棒控制理论在倾斜转弯导弹中的应用［M］.北京：国防工业出版社，2001：12－13.

［5］陈欣，杨一栋，张民.一种无人机姿态智能PID控制研究［J］.南京航空航天大学学报，2003，35（6）：23－24.

［6］江燕俊，周军，林鹏.高超音速BTT巡航飞行器变结构控制系统设计［J］.计算机仿真，2009，26（12）：73－76.

［7］李扬，陈万春.高超声速飞行器BTT非线性控制器设计与仿真［J］.北京航空航天大学学报，2006，32（3）：30－33.

［8］Schumacher，Darren Andrew，PH.D.Tactical missile autopilot design using nonlinear control［D］.America：The university of Michigan，1994：87－89.

［9］Vadim I Utkin，De Shiou Chen，Hao Chi Chang.Block control principle for mechanical systems［J］.Journal of Dynamic Systems measurement and Control，2000，122（1）：1－10.

［10］吕强，郭善亮，王冬来，等.基于DSP四旋翼飞行器姿态控制系统硬件设计［J］.计算机与数字工程，2011（7）.

［11］胡云安，晋玉强，查旭.BTT导弹块模型的鲁棒自适应设计［J］.宇航学报，2004，25（2）：225－229.