一种新的有源网络可靠性参数及其算法

李瑞莹，党 炜

(1.北京航空航天大学可靠性与系统工程学院，北京100191;2.北京航空航天大学可靠性与环境工程技术重点实验室，北京100191;3.中国科学院空间应用工程与技术中心，北京100094)

随着科技的迅速发展，通信网络、电力网络、交通网络已经成为人们生产、生活不可缺少的一部分.对网络定量与定性特征的科学理解，已成为网络时代科学研究中一个极其重要的挑战性课题，甚至被称为“网络的新科学”［1］.网络在建立起物质、信息、能量传递桥梁的同时，也为故障传播提供了条件.网络可靠性水平对网络能否正常运转起着至关重要的作用，一旦网络故障，就可能造成重大甚至是灾难性的影响.因此，网络可靠性成为了网络定量理解中的重要问题.1955年，Lee在对电信交换网络的研究过程中首次定义了连通可靠性，开启了网络可靠性的研究.根据网络中有没有固定的源点，网络可分为无源网络和有源网络.D.R.Shier［2］总结了有源网络的3类网络可靠性参数，包括Moore和Shannon提出的“ST可靠度”、“SAT可靠度”以及Moskowitz提出的“SKT可靠度”.这3类参数已成为有源网络的经典可靠性参数，数十年以来，研究者一直致力于这些参数的算法研究，如J.L.Cook和J.E.Ramirez-Marquez［3］提出了基于蒙特卡洛仿真的无线网络ST可靠度算法;R.Mishra 和 S.K.Chaturvedi［4］提出了一种基于不交积的无冗余ST可靠度算法等等，文献［5］对此进行了详细的综述.然而，上述参数仅能描述源点到指定端点集中所有端点间的连通概率(即将故障判据为“与指定端点集中任意端点失去连通路径”)，却无法对指定端点集中部分端点的连通能力进行度量.现实生活中，往往仅需要了解源点与部分端点间的连通能力是多少，而并不需要确切地知晓源点与具体哪些端点失去了连接.例如，移动通信需要实现90%用户的接入能力，却并不太关心这些用户是谁;又如野战通信网的故障判据［6］为网络内15%的端点传输中断，该判据与传输中断端点数量有关、与具体端点无关.

文中在ST、SAT、SKT这3类有源网络可靠性参数的基础上，提出一个新的有源网络可靠性参数——S(k/N)T可靠度，详细说明该参数的度量范围及与经典参数的关系，并通过“组合连通集-寻找K树-应用容斥原理计算”的方法为该参数给出一种精确算法，最后用案例进行应用说明.

1 基本概念

1.1 经典有源网络可靠性参数

对有源网络G(V，E)，其中V是网络中的端点集，E是链路集.G(V，E)的经典可靠性参数包括［2］:① ST 可靠度(source-to-terminal reliability):用于度量网络中两个端点s和t(s∈V，t∈V且s≠t)之间保持连通的概率;② SAT可靠度(source-to-all terminal reliability):用于度量网络中源点s(s∈V)和网络中其他所有端点之间保持连通的概率;③SKT可靠度(source-to-K-terminal reliability):用于描述网络的源点s与指定端点集K(s∈V，s∉K且K⊂V)中全部端点保持连通的概率.

由此可知，ST可靠度和SAT可靠度分别是SKT可靠度在k=v-1(k，v分别为端点子集K的端点数和网络G(V，E)的端点总数)和k=1时的特例.

1.2 新的有源网络可靠性参数

S(k/N)T可靠度是为了考察有源网络中指定端点集K中部分端点的连通能力而提出的，其定义如下:S(k/N)T可靠度指网络G(V，E)在规定条件下和规定时间内，某个指定端点s与端点子集N中至少k个端点之间能连通的概率，记作RS(k/N)T(t)，其中，N⊂V，s∈V且s∉N.

特殊地，当k=n时，S(k/N)T可靠度就是SKT可靠度;当k=v-1时，S(k/N)T可靠度就是原来的SAT可靠度;当n=1时，S(k/N)T可靠度就是ST可靠度.这也就是说，SKT可靠度、SAT可靠度和ST可靠度是S(k/N)T可靠度的特殊情况.新参数在有源网络可靠性参数中的位置如图1所示.

图1 新参数与其他有源网络可靠性参数的关系

S(k/N)T可靠度可表示为

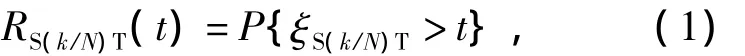
式中:RS(k/N)T(t)是t时刻网络G(V，E)的S(k/N)T可靠度;ξS(k/N)T是指定端点s与端点子集N中能相互连通的端点个数少于k前的工作时间;t是网络规定的时间.

2 算法

网络可靠性的算法包括2类:一类是精确算法，如状态枚举法、容斥原理法、不交积和法、因子分解法等［7］;另一类是近似算法，包括图变换法［8］、定界法［9］等.

对于SKT可靠度，直接的计算方法是枚举网络中所有K树(这里指能使源点s与指定端点集K连通的最小的链路和端点的集合)［10］，再对这些K树进行不交化运算从而求出网络的SKT可靠度.对于文中提出的S(k/N)T可靠度，可以枚举出指定端点集N中k个端点的组合Ki，只要源点s与任意Ki连通，则S(k/N)T可靠性的连通条件就得到了满足，由此将问题转化为SKT可靠度求解问题.考虑到容斥原理法的简洁性和计算效率，文中首先给出基于容斥原理的算法.

2.1 假设

算法的2点假设:① 各端点、链路间故障相互独立;②各端点、链路只有故障、正常两种状态.

2.2 基于容斥原理的算法

将S(k/N)T可靠性的连通条件化解为若干个K树随后再应用容斥原理便可计算出网络的S(k/N)T可靠度.由此，基于容斥原理的算法步骤如下:

1)列举从端点子集N中任意取k个端点的组合，若N中共有n个端点，则共有Ckn种组合，记作K1，K2，…，KCkn.将源点s与Ki结合起来，得到新的集合K'i=Ki+{s}.

该部分算法可表述如下:

Combine(G，N，k，s)

∥生成从指定端点集N中n个端点中选k个端点的所有组合，并与源点s组合在一起

∥输入:指定端点集合N的端点个数n、需要选出的端点个数k

∥输出:返回Ckn种端点组合K'i

fori←1 tokdo

K'［i］←i

K'［i+1］←n+1∥集合K与源点s合并

w riteK'

whileK'［1］＜n-k+1 do

∥递归算法，返回下一个组合

j←k

whileK'［j］＞ =n-k+jdo

j←j-1i←j

K'［i］←K'［i］+1

forj←i+1 tokdo

K'［j］←K'［j-1］+1

w riteK'

显然，上述组合求解算法复杂度为O(n2).

2)根据图G(V，E，Φ)中的链路集E，找出连接集合Ki中各端点的链路集Ei，二者共同构成图G(V，E，Φ)的子图Gi(K'i，Ei，Φi).子图Gi通过邻接矩阵A和关联矩阵M表示.

下面求解对于子图Gi中的树，也就是求解SKT可靠度过程中的K树.由于“G是一棵树”与“G是连通的，且其中链路数=端点数-1”等价［11］，可知图Gi中树的链路数为k.对这些链路集Ei求解k条链路的组合，再检查这些链路的组合是否能满足端点集K'i中任意两个端点连通的条件，检查时可采用深度优先遍历，如无法遍历则去掉该链路组合.剩余的链路组合即是Gi的树，分别记作{Gi1，Gi2，…，Gij}，将这些树合并成{G1，G2，…，Gr}.

对每个K子图Gi求解K树的算法可表述如下:EnumerateKTree(G，K')

∥K树的枚举算法

∥输入:图G(V，E，Φ)，端点组合Ki'

∥输出:K树Gij

m=0

fora←1 ton+1 do

forb←1 toa-1 do

ifa∈Ki'andb∈Ki'

A［a］［b］←Φ ∥邻接矩阵

If A［a］［b］≠0

m=m+1 ∥链路条数计数

else

A［a］［b］←0

∥求解从m条链路选取k条组合，并检查是否满足连通条件

j=0

forp←1 tokdo

E［p］←p

con=0 ∥连通个数计数

DFS(Ki'，E，v) ∥深度优先遍历

ifcon=k

j=j+1

Gij←E+Ki'

w riteGij

whileE［1］＜m-k+1 do

∥递归算法，返回下一个组合

q←k

whileE［q］＞ =m-k+qdo

q←q-1p←q

E［p］←E［p］+1

forq←p+1 tokdo

E［q］←E［q-1］+1con=0

DFS(Ki'，E，V)

ifcon=k

j=j+1

Gij←E+Ki'

w riteGij

DFS(Ki'，E，v) ∥v为起始端点

∥在Ki'与E组成的图中，通过深度优先遍历，检查任意两个节点间是否存在链路

Visited(v)←1con←con+1

for邻接于v的每个端点wdo

ifVisited(w)=0

DFS(Ki'，E，w)

显然，上述组合求解算法复杂度也为O(n2).

3)采用容斥原理计算S(k/N)T可靠度，算法如下:

3 示例

3.1 示例说明

以图2所示网络拓扑结构G(V，E，Φ)为例计算S(k/N)T 可靠度.其中，V={v1，v2，v3，v4}，E={e1，e2，e3，e4，e5}，Φ(e1)=v1v2，Φ(e2)=v1v3，Φ(e3)=v2v3，Φ(e4)=v2v4，Φ(e5)=v3v4.将网络中各端点可靠度记为Rvi(i=1，2，…，4)，链路可靠度记为Rej(j=1，2，…，5).令v4为源点，N={v1，v2，v3}，k=2，求解S(k/N)T可靠度

图2 示例的网络拓扑结构

3.2 基于容斥原理的计算

下面按照第2节中基于容斥原理的网络S(k/N)T可靠度计算方法进行计算:

1)列举从端点子集N={v1，v2，v3}中任意取2个端点的组合，即满足S(k/N)T连通的各种组合，有C23=3 种，分别是K1={v1，v2}，K2={v1，v3}，K3={v2，v3}.令K'i=Ki+{v4}，即K'1={v1，v2，v4}，K'2={v1，v3，v4}，K'3={v2，v3，v4}.

2)根据图G(V，E，Φ)，找出连接集合K'i中各端点的链路集Ei，得到子图Gi如图3所示.

图3 子图Gi

对子图Gi求解K树.对G1和G2，由于子图链路数恰等于k=2，且链路集合E能保证端点集K'1和K'2中任意两个端点间连通，故子图G1和G2对应的K树如图4a，4b所示.对于G3，通过链路组合和通性检验可知，其对应的K树如图4c所示.

图4 子图Gi对应的K树

3)采用容斥原理对S(k/N)T可靠度的计算如下:

若令网络中各端点可靠度相同，为0.90，链路可靠度也相同，为0.99，根据式(3)，可得

图5反映了端点和链路可靠度变化对本案例网络S(k/N)T可靠度的影响.其中图5a是链路可靠性不变的情况下，网络S(k/N)T可靠度随端点可靠度的变化;图5b是端点可靠性不变的情况下，网络S(k/N)T可靠度随链路可靠度的变化.

由图5可以看出，端点可靠度的变化对网络S(k/N)T可靠度有较大的影响，从优化网络可靠性的角度应优先提高端点可靠度.

4 结论

1)针对现有的有源网络可靠性参数无法度量源点与指定端点集中部分端点间连通概率的问题，提出了S(k/N)T可靠度这一新的有源网络可靠度参数.

2)基于容斥原理法给出了该参数的精确计算方法，通过转化S(k/N)T可靠性的连通条件解决了S(k/N)T可靠度的计算问题.该算法适用于系统二态性、故障独立性假设前提，同时考虑了端点故障和链路对网络可靠性的影响.

3)文中提出的基于容斥原理的算法尚存在计算复杂度大，不适用于大规模网络应用的问题.从已经开展的网络可靠性各类参数的精确算法研究可知，这一问题难以通过精确计算的方法解决.因此，对于大规模网络的计算还需结合SKT可靠度的近似算法进一步的研究.

References)

［1］ Watts D J.The ″new″science of networks［J］.Annual Review of Sociology，2004，30:243-270.

［2］ Shier D R.Network Reliability and Algebraic Structures［M］.Oxford:Clarendon Press，1991.

［3］ Cook JL，Ramirez-Marquez JE.Reliability for clusterbased Ad-hoc networks［C］∥Proceedings of Annual Reliability and Maintainability Symposium.Las Vegas:IEEE，2008，doi:10.1109/RAMS.2008.4925802.

［4］ Mishra R，Chaturvedi S K.A cutsets-based unified framework to evaluate network reliability measures［J］.IEEE Transactions on Reliability，2009，58(4):658-666.

［5］ 江逸楠，李瑞莹，黄 宁，等.网络可靠性评估方法综述［J］.计算机科学，2012，39(5):9-13，18.Jiang Yinan，LiRuiying，Huang Ning，et al.Survey on network reliability evaluation methods［J］Computer Science，2012，39(5):9-13，18.(in Chinese)

［6］ 中国人民解放军总装备部.GJB 1909A:装备可靠性维修性保障性要求论证［S］.2009.

［7］ Terruggia R.Reliability analysis of probabilistic networks［D］.University of Turin，2010:33-42.

［8］ Rebaiaia M L，Ait-Kadi D，Merlano A.A practical algorithm for network reliability evaluation based on the factoring theorem:a case study of a generic radiocommunication system［J］.Journal of Quality，2009，16(5):323-336.

［9］ Mohamed M H S，Yang Xiaozong，Liu Hongwei，et al.An efficient algorithm for reliability lower bound of distributed systems［J］.World Academy of Science，Engineering and Technology，2009，27:40-42.

［10］ 王 芳，侯朝桢.大型网络的SKT可靠性的分散计算法［J］.计算机工程，2003，29(18):18-19，156.Wang Fang，Hou Chaozhen.Using decomposition method to calculate SKT reliability of large-scale network［J］.Computer Engineering，2003，29(18):18-19，156.(in Chinese)

［11］ 李晓明，黄振杰.图中树的数目:计算及其在网络可靠性中的作用［M］.哈尔滨:哈尔滨工业大学出版社，1993:114.