基于投影修正和POCS的图像超分辨率重建

杨 欣，唐庭阁，费树岷，周大可

(1.南京航空航天大学自动化学院，江苏南京210016;2.东南大学自动化学院，江苏南京210096)

数字图像的获取受硬件设备，外界环境以及成像技术等因素的影响，图像质量下降，分辨率不高.因此，超分辨率技术应运而生.所谓的超分辨率技术(super resolution，SR)［1］，就是通过将多幅模糊，变形，空间微位移，频谱混叠的低分辨率图像(或视频序列)中有用信息的抽取，融合估计出一幅较高分辨率图像.其在医学诊断，交通管理，视频监控，远程遥感以及获取军事情报等方面有着广泛的应用.

20世纪60年代，超分辨率重建技术最早是由Harris和Goodman基于单幅图像复原的概念提出.后续的研究分为2类［2］:频域法和空域法.空域算法主要包括迭代反向投影法［3］(iterative back projection，IBP)，邻域嵌套方法［4］(neighbor embedding，NE)，凸集投影法［5］(projections onto convex sets，POCS)等.

空域方法中，POCS算法是一种广泛使用的重建方法.Xie Wei等［6］提出估计子像素位移并进行运动补偿的POCS盲图像复原算法.陈光盛等［7］将MAP方法和POCS方法结合起来，获得了较好的效果.肖创柏等［8］提出改进PSF系数的POCS算法，有效地抑制了边缘Gibbs现象.田敬北等［9］引入时空联合自适应机制设计自适应残差阈值，有效减缓了错误运动估计信息对重建图像的影响.

传统POCS算法中残差阈值通常选为常数，点扩散函数通常选为单一的高斯模糊函数，对全局的迭代投影采用相同程度的一致性约束，造成某些位置出现欠投影或过投影，从而形成边缘振荡效应，即Gibbs效应.

文中提出一种采用投影修正抑制Gibbs效应的超分辨率重建算法.该算法在传统POCS重建算法的基础上，通过在每一次的迭代过程中结合边缘约束和前后重建图像的差值获得能够反映欠投影和过投影信息的投影修正算子，利用该算子对残差阈值和点扩散函数进行修正，从而实现投影修正的POCS算法.试验证明文中算法能够在保持边缘细节信息的前提下，有效抑制Gibbs效应，获得更好的重建效果.

1 POCS算法

低分辨率图像的超分辨率重建可表达［10］为

式中:yk表示大小r1×r2的LR图像;z表示大小为r1N×r2N的HR图像，为采样因子;H表示点扩散函数(point spread function，PSF)，即退化矩阵;nk为噪声.

POCS算法将待求高分辨率图像^z看做成像空间Rr1×r2中的未知向量，先验信息和约束条件被描述为成像空间中的一个凸集 Ci∈Rr1×r2，i=1，2，…，m.对于每一个凸集Ci定义相应的凸集投影算子Pi.POCS的基本思想就是利用凸集投影算子Pi对高分辨率图像的初始估计^z0进行反复迭代投影，获得理想高分辨率图像.通常采用插值法构造高分辨率图像的初始估计^z0，利用观测序列的约束集修正^z0，直至满足迭代终止条件.由POCS算法重建高分辨率图像^z的基本表达式为

2 基于投影修正的POCS重建算法

2.1 边缘约束算子E

设^z0为初始高分辨率图像，^z0(s，t)为位于(s，t)的像素值.文中算法对^z0计算2阶方向差分，得到图像的边缘约束算子E.2阶方向差分法如下:

式中:Ev(s，t)和Eh(s，t)分别是垂直和水平方向的差分算子Ev和Eh相应位置的像素值，令边缘约束算子E为二者之和.算子E以数值的大小呈现图像的边缘结构特征，较小值对应平缓区域，较大值对应边缘区域.

2.2 投影修正算子M

POCS算法中每一次投影前后重建结果的差值反映了本次投影信息，即凸集约束集合对^zn所作的修正.传统POCS算法的投影方法采用固定的残差阈值和单一的点扩散函数，不能对所有位置做出适当的修正，某些位置可能出现欠投影或过投影，从而导致了Gibbs效应.由于Gibbs效应主要发生在边缘位置附近，因此将全部投影与边缘约束算子E作用的投影进行“差运算”，即可分离出欠投影与过投影.为标识这些不恰当投影的位置与程度信息，文中算法定义投影修正算子M如下:

式中:M(s，t)和E(s，t)分别是修正算子M和边缘约束算子E位于(s，t)的值;‘·’运算符代表‘矩阵点乘’;^zn+1(s，t)和 ^zn(s，t)分别表示第n+1 次重建图像和第n次重建图像;ε为修正因子，作用是令M中的数据取值范围为［0，1］;max(M)表示矩阵M中最大值.

2.3 投影修正过程

POCS算法中常见的约束集有数据一致性约束，幅值约束等.令^zn(s，t)表示当前估计的高分辨率图像 ^zn中位于(s，t)处的像素值，yk(i，j)表示低分辨率图像yk中位于(i，j)处的像素值，数据一致性约束集可定义为

式中:R(i，j)为残差;δ0为残差阈值，传统 POCS算法δ0常设为常数.

1)修正残差阈值δM

在数据一致性约束中，残差阈值大小与修正的程度成反比，考虑算子M每个位置的值标志着该处错误投影的程度，对于这些位置应该相应的进行不同程度的修正，因此文中算法对残差阈值进行修正.定义新的残差阈值矩阵δM为

式中:δM(s，t)为 δM中位于(s，t)的值;δ(s，t)为与M相同尺寸的矩阵中位于(s，t)的值，且 δ(s，t)中元素均为残差阈值δ0;参数α用于调节残差阈值的修正程度，通常α可取20～30.

2)修正点扩散函数HM

假设低分辨率图像yk中的某像素(i，j)映射到高分辨率图像^zn中相应位置为(s'，t')，则残差R(i，j)的定义式为

式中:H(s，t;i，j)为点扩散函数H相应位置的值;H通常选为高斯模糊核函数;ω为模板尺寸.式(7)中等式右侧第1部分为低分辨率图像真实值，第2部分为根据降质过程获得的模拟值.若残差R(i，j)为正且大于残差阈值δ0，说明当前估计值^zn(s，t)偏小，应对^zn(s，t)增大修正，反之减小修正.由残差R(i，j)和残差阈值δ0的关系定义数据一致性约束的投影算子PD如下:

传统POCS算法中点扩散函数H通常选用高斯模糊核函数，而单一的选择模糊核函数无法对现实世界中图像模糊化过程进行全面模拟，文献［10］中采用模糊核函数库遍历的方法获得较好的恢复效果.图像重建研究中，常用的模糊核函数有高斯模糊，离焦模糊等，表达形式为

文中针对POCS算法分别采用两种模糊核函数进行试验，对结果分析发现采用高斯模糊核函数重建结果边缘细节较清晰，但是Gibbs效应明显，而采用离焦模糊核函数重建结果能较好地抑制Gibbs效应.基于此，文中算法通过对投影修正算子M进行基于局部方差的区域分析，从而修正点扩散函数，局部均值mM和局部方差σ2M(i，j)的计算方法如下:

通过试验观察，局部方差σ2M(i，j)和Gibbs效应密切相关，σ2M(i，j)越大，Gibbs效应越明显，这说明区域局部方差σ2M(i，j)越大，错误投影程度越大.因此在算子M中错误投影严重的区域点扩散函数选用离焦模糊核函数，其余则选用高斯模糊核函数.具体形式如下:

式中:HM(s，t;i，j)为修正的点扩散函数HM相应位置的值;β为调节两种模糊核函数所占比重的参数，通常取0.8～1.2，决定了点扩散函数的形式后，在实际应用中还应对其进行归一化处理.

2.4 图像重建

获得修正后的残差阈值δM和点扩散函数HM之后，将其代入式(7)和式(8)即可得到修正的残差阈值RM(i，j)和数据一致性约束投影算子PDM，如下:

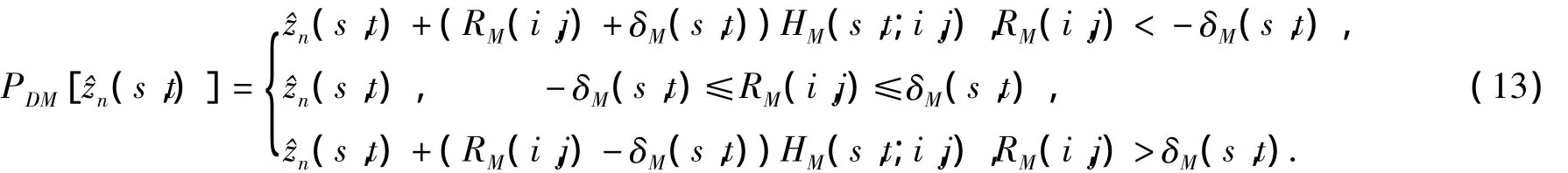
另根据先验知识“8 bit图像的取值范围为［0，255］”可定义幅值约束凸集CA为

其相应的幅值约束投影算子PA为

完成相应约束凸集及其投影算子的定义之后，代入式(2)即可得到具体的投影修正POCS重建方法:

2.5 详细算法

1)初始化:最大迭代次数nMAX，点扩散函数H，残差阈值δ0，由配准法进行运动估计，获得配准参数，双线性插值获得初始高分辨率图像^z0，根据式(3)计算边缘约束算子E.

2)根据式(7)，计算残差R(i，j)，根据式(8)和(15)，分别对模拟高分辨率图像进行数据一致性约束投影修正和幅值约束投影修正，获得模拟高分辨率图像^zn+1.

3)根据式(4)，(6)，(11)及当前HR图像^zn+1，前次模拟高分辨率图像^zn，计算投影修正算子M，修正残差阈值δM，修正点扩散函数HM.

4)根据式(12)，(13)，利用修正的残差阈值δM和点扩散函数HM计算一致性约束投影算子PDM，代入式(16)获得高分辨率图像^zn+1.

5)若n+1＜nMAX，转到步骤3)，否则程序结束，最终的^zn+1即为重建图像zn+1.

3 试验结果与分析

根据文中提出的基于投影修正的POCS算法，选用6幅大小为256×256像素的图像作为试验对象进行测试，并对所有试验对象做平移，模糊，降采样等处理，分别生成5幅低分辨率图像.模糊函数采用尺寸为3×3，方差为1的高斯模糊，降采样采用1/2的行列抽样，运动估计采用keren配准方法.为衡量算法性能，在客观评判标准方面选用常用的峰值信噪比(peak signal to noise ratio，PSNR)［10］进行评判.在试验中取迭代次数nMAX=5，残差阈值调节参数α=30，点扩散函数调节参数β=1，初始残差阈值δ设置较低时，有利于图像恢复，但是同噪声及Gibbs效应也更严重，因此，文中以δ=3和δ=5分别进行两组试验，试验所得的峰值信噪比数据如表1所示.

表1 算法改进前后峰值信噪比

由表1的数据可知，在δ=3和δ=5两种情况下，文中算法的客观数据均优于传统POCS算法.为了进一步验证试验效果，列出在δ=3和δ=5两种情况下，3幅图像的视觉效果对比如图1所示.

图1的2个子图中第1排3幅图是传统POCS算法重建结果，第2排是文中算法重建结果，可以看出，传统POCS算法重建结果在图像边缘附近有明显的Gibbs效应，而文中算法对Gibbs效应取得了不错的抑制效果，重建图像质量更好.

由上述试验可知，文中算法中的残差阈值调节参数α和点扩散函数调节参数β的选取会对试验结果产生影响，具体分析如下.

1)残差阈值调节参数α的影响

参数α用于调节残差阈值δ的修正程度，若α太小，则起不到对δ的修正作用，无法实现Gibbs的抑制;若α过大，导致残差阈值整体过大，则式(13)中POCS算法对真实值与模拟值的数据一致性投影修正失去意义.

2)点扩散函数调节参数β的影响

参数β用于调节高斯模糊核函数和离焦模糊核函数在点扩散函数的选取中所占的比重，它根据算子M相应区域错误投影程度决定模糊核函数的选取.β过小或过大都会导致某一种模糊核函数的过度使用用，造成重建图像Gibbs效应严重或是过度模糊.

图1 算法改进前后视觉效果对比

4 结论

1)算法在传统POCS重建算法的基础上做出改进，获得能够反映欠投影和过投影信息的投影修正算子.

2)对残差阈值和点扩散函数进行修正，有效抑制了Gibbs效应.仿真试验证明了文中算法在客观数据和视觉效果方面都优于传统POCS算法.

3)文中算法尚存在一些问题，譬如算法复杂程度增加，导致程序运行时间变长;一些参数的选取不当会导致重建效果变差，这些问题都会在以后的研究中解决.

References)

［1］ Farsiu S，Robinson D，Elad M，et al.Advances and challenges in super-resolution［J］.International Journal of Imaging Systems and Technology，2004，14(2):47-57.

［2］ van Ouwerkerk JD.Image super-resolution survey［J］.Image and Vision Computing，2006，24(10):1039-1052.

［3］ Qin Fengqing，He Xiaohai，Chen Weilong，et al.Video super-resolution reconstruction based on subpixel registration and iterative back projection ［J］.Journal of Electronic Imaging，2009，doi:10.1117/1.3091936.

［4］ Chang Hong，Yeung D Y，Xiong Yimin.Super-resolution through neighbor embedding［C］∥Proceedings of the2004IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE Computer Society，2004:1275-1282.

［5］ Tian B，Sclabassi R J，Hsu JT，et al.POCS superresolution image reconstruction using wavelet transform［C］∥Proceedings of2004International Symposium on Intelligent Signal Processing and Communication Systems.Seoul:IEEE，2004:67-70.

［6］ Xie Wei，Zhang Feiyan，Chen Hao，et al.Blind superresolution image reconstruction based on POCSmodel［C］∥Proceedings of2009International Conference on Measuring Technology and Mechatronics Automation.Zhangjiajie，China:IEEE Computer Society，2009:437-440.

［7］ 陈光盛，李树涛.MAP和POCS算法实现超分辨率图像的重建［J］.科学技术与工程.2006，6(4):396-399.Chen Guangsheng，Li Shutao.Reconstruction of superresolution image using MAP and POCS algorithms［J］.Science Technology and Engineering，2006，6(4):396-399.(in Chinese)

［8］ 肖创柏，段 娟，禹 晶.序列图像的POCS超分辨率重建方法［J］.北京工业大学学报，2009，35(1):108-113.Xiao Chuangbai，Duan Juan，Yu Jing.POCS super-resolution reconstruction from image sequences［J］.Journal of Beijing University of Technology，2009，35(1):108-113.(in Chinese)

［9］ 田敬北，侯天峰，李梦和.基于POCS框架的时空联合自适应视频超分辨率重建算法［J］.计算机应用研究，2011，28(7):2778-2781.Tian Jingbei，Hou Tianfeng，Li Menghe.Spatio-temporal adaptive super-resolution reconstruction of video based on POCS frame ［J］.Application Research of Computers，2011，28(7):2778-2781.(in Chinese)

［10］ 杨 欣，王从庆，费树岷.基于最大后验概率的SAR图像自适应超分辨率盲重建［J］.宇航学报，2010，31(1):217-221.Yang Xin，Wang Congqing，Fei Shumin.An adaptive technology for SAR image blind super-resolution based on MAP［J］.Journal of Astronautics，2010，31(1):217-221.(in Chinese)