复杂环境中交通标志的实时识别方法

缪小冬，李舜酩，沈 峘，余宏兵

(1.南京航空航天大学能源与动力学院，江苏南京210016;2.合肥通用机械研究院，安徽合肥230031)

道路交通标志是重要的道路安全设施，在规范交通行为，引导车辆及行人顺利通行，保障道路安全等方面具有重要作用.近年来，随着社会经济的发展，交通环境变得愈加复杂，人们期望能够出现一种智能化的视觉辅助导航设备，能够自动识别交通标志信息，帮助驾驶员以及色弱人群对道路上的状况做出预判，从而提高交通安全性.这也是智能车辆及智能交通的关键技术之一.如何有效地进行交通标志识别存在着很多问题，例如曝光不均、尺度变化、遮挡、角度、模糊等，其中光照带来的亮度不均是最常见的影响因素，一般通过提高硬件性能和算法改进来解决.由于图像传感器的高性能与成本息息相关，因此，采用性价比合理的硬件平台，尽量提高算法在复杂光照环境下的鲁棒性和实时性成为人们的研究重点［1］.迄今为止，前人已经在此领域做了大量的研究，主要考虑了交通标志的颜色和形状差异，并通过关键点匹配以及神经网络等方法进行分类识别.Y.Y.Nguwi等［2］以颜色作为特征，采用 Resillient反向传播神经网络和尺度共轭梯度算法，对自身数据库的识别准确率为95.96%，但对于光照差异大的目标容易出现误判，算法效率不理想.A.de la Escalera等［3］认为交通标志是由颜色能量，彩色能量，梯度能量和距离能量等先验知识组成的，他采用了遗传算法和模拟退火算法.以他们课题组采集的数据为测试对象，遗传算法的识别率为90.4%，退火算法的识别率为82.9%.X.W.Gao等［4］利用CIECAM97颜色空间，并结合形状信息，设计了一种基于模板相似度匹配的识别方法.对英国交通标志的识别率为95%，牺牲了一定的计算效率，对于曝光不均匀的目标容易出现识别误差.C.Bahlmann等［5］采用Harr小波提取特征，然后用Adaboost来训练，通过层次贝叶斯模型进行样本分类，在标准PC机上计算效率为10帧·s-1，但识别率受样本质量的影响较大.X.Baró等［6］提出了一种渐进式的adaboost检测方法和多类聚类纠错输出编码方法(Forest-ECOC)，对于不同类型的交通标志识别率大概在90%左右，但对光线较暗以及形状类似情况效果不理想.Fu Mengyin等［7］提供了一种基于有约束的快速二值径向对称检测算法，并采用基于伪Zernike特征提取的支持向量机进行目标分类，算法在Lab颜色空间进行，对径向对称以外的交通标志缺乏测试数据.由此可以看出，这些方法主要采用颜色和形状特征，难以满足复杂曝光情况下的交通标志识别，如图1所示.

图1 GTSRB数据库的随机样本

在实时性方面也不理想，而根据颜色恒常性理论，物体表面的颜色并不取决于刺激的物理特性和视网膜感受的特性，也就是说，在强曝光的情况下，颜色数值并不能完全反映其本质性质.此外，在不同试验平台上的结果也不具有可比性.针对以上问题，笔者提出一种能够有效消除尺度影响和曝光的交通标志识别方法，并在标准的数据库中进行测试.首先，提出一种基于Log Gabor小波的多分辨率特征提取方法，实现多尺度特征的提取，再将其与相位一致性相结合，提取出多尺度相位信息，然后选择数据库中的部分数据进行样本学习，得到43个支持向量，最后将这些支持向量用于剩余数据的测试，输出结果与原标记进行比较，通过将识别结果与其他几种典型方法进行对比，说明该方法的有效性.

1 特征提取

1.1 Log Gabor小波

Gabor滤波器已被广泛应用于图像的纹理分析等方面，这是因为Gabor小波具有良好的方向和频率选择特性，同时它能够达到空域和频域联合测不准原理的下限.但是Gabor函数不是严格带通，并且其最大带宽被限制在1倍频，因此A.Koncar［8］提出了Log-Gabor函数，并证明，对数频率尺度上传递函数为高斯函数的滤波器可以对图像进行更有效地编码，也就是说，对数Gabor函数能更真实反映自然图像的频率响应.在线性频率尺度上，Log Gabor函数的传递函数为

式中:ω0为滤波器的中心频率;为了保证滤波器的形状恒定，对于不同的中心频率必须保持不变，例如为0.74时，大致相当于子滤波器为1倍频的带宽，为0.55时相当于2倍频，0.41相当于3倍频.

与Gabor函数相比，Log Gabor函数有2个重要特征:①没有直流分量，因此，图像处理时不受亮度条件的影响;②Log函数的传递函数在高频段有较长的冗余量，可以填补普通Gabor函数低频信息冗余.D.J.Field等［9］关于自然图像统计的研究显示，自然图像的幅度大约在1/ω处逐渐衰落，对具有这种谱特征的图像编码，必须使用具有相似谱的滤波器，存在延拓的Log Gabor函数能够更有效地对自然图像进行编码，并且Log Gabor更符合人的多尺度视觉模型，图2为Log Gabor的实部和虚部.

图2 Log Gabor(8个方向，5个尺度)

1.2 相位一致性

虽然Log Gabor能够很好地模拟出类似人眼的多尺度模型，但是实际环境中，克服光照不均对于目标的识别是最需要解决的问题.由于相位一致性的模型不是基于局部亮度梯度，而是假定图像相位中极大值的点被感知，因此其能有效地遏制曝光不均对交通标志的影响［10］.

以某一维信号I的傅立叶展开为例.

式中:An为第n个余弦分量的振幅;ωx为常数，一般取2π;φn0为第n个分量的相位偏移量;φn(x)表示在x位置傅立叶变换的局部相位.

将相位一致性定义为

式中:¯φ(x)为相位的加权平均值.

为了简化，可从能量角度求解PC函数，令

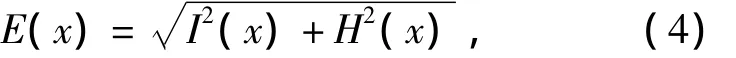
式中:I为实部;H为虚部.

而PC函数与能量函数的关系可以表示为

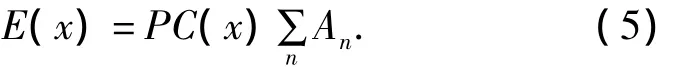
将原始信号和Gabor进行卷积可以完成信号的特征提取.如果Men表示偶小波，Mon表示奇小波，则信号I的振幅为

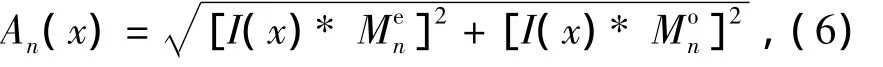
相位表达为

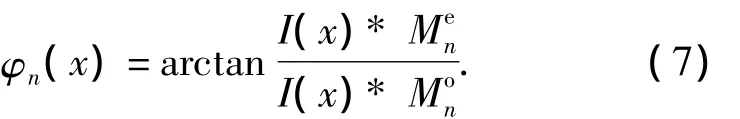
用偶小波和信号的卷积的结果近似表示去掉DC分量的信号F(x)，相应地，F(x)的希尔伯特变换H(x)可近似用信号和奇小波卷积之和表示:

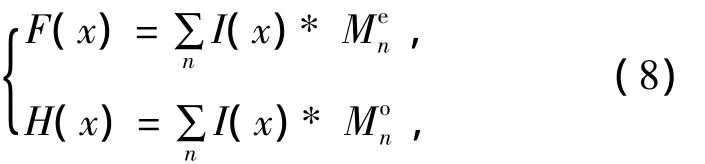
根据上式可以求出PC函数为

式中ε可以防止分母为0.

由式(9)可知:局部能量的峰值与PC函数峰值相对应;PC函数是能量和幅值的比值，量纲为1，因此不受图像亮度变化的影响.

1.3 Log Gabor小波对相位一致性的表达

由于在相位一致性中，能量E与相位角的余弦有关，而当φn(x)和¯φ(x)相等时，余弦函数最大，即能量最大，只有在¯φ(x)±25°时，无论¯φ(x)取何值，都为常量，从而使 PC对相位差的余弦值不敏感［11］.为此，构造了PC函数对相位角敏感的函数，使相位角的差值分布在0～±π/2之间，计算公式表示为

结合式(1)和式(10)提取出来的Log Gabor小波的相位一致性特征可以用来有效地描述交通标志，抑制曝光和尺度变化的影响［12］.

采用不同方法对目标提取的结果如图3所示，图3a为曝光不均情况下采集到的交通标志图，图3b，c，d 分别为采用 Gabor，Log Gabor以及融合 Log Gabor和相位一致性的检测方法，可以看出，第3种方法要优于直接用前2种方法，较好地抑制了光照不均对目标特征提取的影响.

图3 采用不同方法对目标提取的结果

2 分类器设计

分类器的种类比较多，目前能够满足工程应用的主要有基于模板匹配和机器学习的方法，由于模板匹配的计算难以兼顾计算量和鲁棒性的要求，因此机器学习是目前交通标志识别应用的主流.其中，SVM，神经网络，决策树，贝叶斯分类，Adaboost，隐马尔可夫过程等理论被广泛地研究及应用［13］.由于支持向量机具有完善的理论基础和更为出众的性能，在许多领域得到了更广泛的关注.

2.1 支持向量机

支持向量分类机由Vapnik等提出，是由线性可分情况下最优分类器发展而来，基本思想为对2类不同的数据样本，找出1个分类线，同时满足将2类正确分开，使训练错误率最小，且分类间隔最大.

设样本集合S={(xi，di)}Ni=1，xi∈Rn，di∈{+1，-1}，将输入向量非线性的映射到高维特征空间，通过定义特征空间的维数，即可定义向量使之对未训练样本具有同样的分类效果.线性判别函数的一般形式为

对应的分类面方程为

将判别函数进行归一化，使2类所有的样本都满足|f(x)|≥1，此时离分类面最近的样本满足|f(x)|=1，如果要求分类面对所有样本都能正确分类，需要满足:

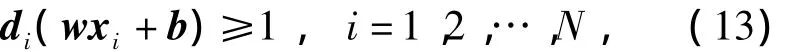
因此，满足上式且使‖w‖2最小的分类面就是最优分类面，应用拉格朗日乘子法，构造拉格朗日函数:

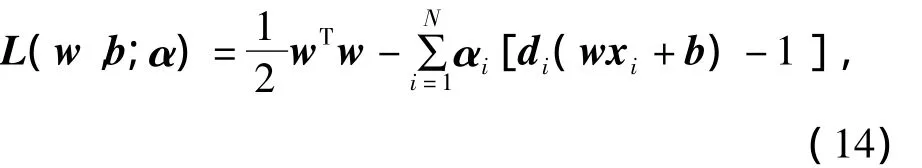
式中:α为拉格朗日乘子.

为了求取式(14)的最小值，可根据KKT(Karush-Kuhn-Tucker)条件，即

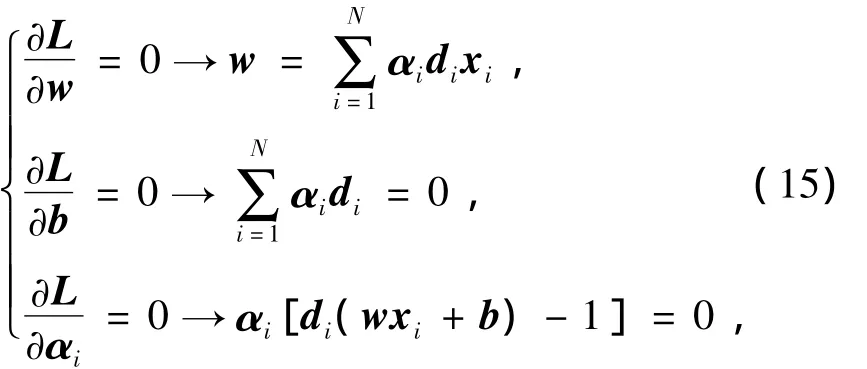
求得最优超平面的决策函数为

式中:b*为分类阈值.

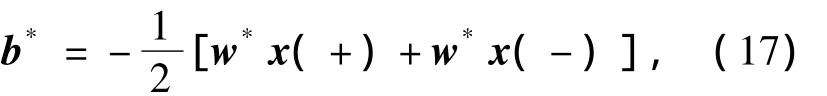
式中:x(+)代表“+”类中1个支持向量;x(-)代表“-”类中1个支持向量.

在线性不可分的情况下，需要通过1个非线性映射把线性不可分的样本空间映射到1个高维的Hilbert空间，使得在原来空间中非线性不可分的问题转化为在特征空间中的线性可分的问题.SVM方法应用核函数解决了计算复杂性的问题，在某种程度上避免了维数灾难.常用的核函数主要有n次多项式函数，Gauss径向基函数，Sigmoid函数.根据经验，选择Gauss径向基函数.

在进行交通标志分类时，给的每个样本由1个向量和1个标记，表示为(xi，yi)，其中xi就是交通标志的特征向量，其维数表示问题的复杂度;yi表示分类标志，只能选择1或者-1，分别意味着属于还是不属于这个类.对于线性分类的问题，SVM分类器通过输入向量的线性函数来实现.

2.2 多分类问题

前文介绍了2分类的情况，在多分类情况下(数量为N)，主要有2种方式:①1对多，②1对1.方法①需要训练N个分类器，第i个分类器是观察属于分类i还是分类i的补集(除去i的N-1个分类).方式②需训练N*(N-1)/2个分类器，分类器(i，j)能够判断某个点是属于i还是属于j，显然前者在检测中的效率更高，因此采用1对多的方法.

由于随意采集的数据不具有可比性，处理的交通标志来源于German Traffic Sign Recognition Benchmark(GTSRB)，这是目前国际上普遍认可的交通标志数据库，能够进行不同识别算法的性能对比，具有43个大类，共144 769个样本［14］.图4为具有代表性的12类，包括速度限制、禁行、取消限制、转向指示、危险警示和特有标志6大项.每一类型的交通标志至少包括200种以上的数据，涵盖了不同尺度，光照，角度，遮挡等情况.

图4 GTSRB数据库中主要的交通标志

测试硬件平台为Intel Core 2.4 GHz CPU，内存2 GB的台式计算机上，软件平台为Matlab 7.0和Libsvm 1.8.由于每一类的样本数并不一致，为了统一测试结果，仅选择每一类的前200个样本，将剩下的前100个样本作为测试对象，识别的结果如果与标定数值相同表明识别正确，如果不同则意味着识别错误.

表1为几种典型方法的识别率，分类器都是SVM.很明显，进行Log Gabor与相位一致性计算后的识别效果要明显好于单独采用Gabor或者Log Gabor的方法，且能很好地保证实时性.

表1 文中方法与传统方法的比较

3 结论

文中方法对6大类主要交通标志样本的平均识别率达到98%;在Intel双核CPU 2.4 GHz硬件平台上，对于数据库中不同尺度的图片处理速度达到28帧·s-1，满足了实时性的要求;很好地克服了光照不均的问题，鲁棒性强，适用于不同曝光条件下的交通标志识别，能够满足实际需求.

References)

［1］ 王 进，康 雄.基于演化硬件的道路限速标志识别方法［J］.江苏大学学报:自然科学版，2011，32(6):689-694.Wang Jin，Kang Xiong.Recognition method of road speed limit sign based on evolvable hardware［J］.Journal of Jiangsu University:Natural Science Edition，2011，32(6):689-694.(in Chinese)

［2］ Nguwi Y Y，KouzaniA Z.Detection and classification of road signs in natural environments［J］.Neural Computation and Application，2008，17(3):265-289.

［3］ de la Escalera A，Armingol JM，Pastor JM.Visual sign information extraction and identification by deformable models for intelligent vehicles［J］.Transaction of Intelligent Transportation System，2004，5(2):57-68.

［4］ Gao XW，Podladchikova L，Shaposhnikov D.Recognition of traffic signs based on their colour and shape features extracted using human vision models［J］.Journal of Vision Communication and Image Representation，2006，17(4):675-685.

［5］ Bahlmann C，Zhu Y，Ramesh V，et al.A system for traffic sign detection，tracking and recognition using color，shape，and motion information［C］∥IEEE Intelligent Vehicles Symposium.Piscataway，USA:IEEE Press，2005:255-260.

［6］ BaróX，Escalera S，VitriáJ，et al.Traffic sign recognition using evolutionary adaboost detection and forest-ECOC classification ［J］.IEEE Transaction of IntelligentTransportation Systems，2009，10(1):113-126.

［7］ Fu Mengyin，Huang Yuanshui，Ma Hongbin.New method for recognition of circular traffic sign based on radial symmetry and pseudo-zernike moments［J］.Journal of Beijing Institute of Technology，2011，20(4):520-526.

［8］ Koncar A，JanBen H，Halgamuge S.Gabor wavelet similaritymaps for optimizing hierarchical road sign classifiers［J］.Pattern Recognition Letters，2007，28:260-267.

［9］ Field D J，Chandler D M.Method for estimating the relative contribution of phase and power spectra to the total information in natural-scene patches ［J］.Journal of the Optical Society of America A:Optics，Image Science，and Vision，2012，29(1):55-67.

［10］ Fischer S，Šroubek F，Perrinet L，et al.Self invertible 2D Log-Gabor wavelets［J］.International Journal of Computer Vision，2007，75(2):231-246.

［11］ Wang Ke，Xiao Pengfeng，Feng Xuezhi，et al.Image feature detection from phase congruency based on two dimensional Hilbert transform［J］.Pattern Recognition Letters，2011，32(15):2015-2024.

［12］ 许廷发，倪国强.基于Log Gabor小波相位一致不变量的目标识别［J］.光电子·激光，2006，17(2):222-225.Xu Tingfa，Ni Guoqiang.Target recognition based on Log Gabor wavelet phase congruency feature invariant［J］.Journal of Optoelectronics·Laser，2006，17(2):222-225.(in Chinese)

［13］ Maldonado-Bascón S，Acevedo-Rodríguez J，Lafuente-Arroyo S，et al.An optimization on pictogram identification for the road-sign recognition task using SVMs［J］.Computer Vision and Image Understanding，2010，114(3):373-383.

［14］ Stallkamp J，Schlipsing M，Salmen J，et al.Man vs.computer:benchmarking machine learning algorithms for traffic sign recognition［J］.Neural Networks，2012，32:323-332.