一种验证软件演化过程行为的代数推导方法

2013-10-09 11:19王黎霞谢仲文

江苏大学学报（自然科学版） 2013年5期

代飞，王黎霞，谢仲文，张璇，朱锐

(1.云南大学软件学院，云南昆明650091;2.云南大学云南省软件工程重点实验室，云南昆明650091;3.云南大学经济学院，云南昆明650091)

软件过程的研究大致始于20世纪80年代中期，以Osterweil于1987年发表的“软件过程也是软件”为代表性著作，自此掀起了“软件过程运动”，并逐步形成软件过程工程.在软件过程领域，软件过程建模和软件过程验证是两大关键活动.软件过程建模是对软件过程进行抽象和表示的活动，方式可以是非形式化、半形式化或形式化的，其目的是建立过程模型［1］.通过对过程模型的认识和分析，增强对过程本身的理解，进而更好地支持软件开发.软件过程验证是检验软件过程模型与过程需求是否一致的活动，方式也可以是非形式化、半形式化或形式化的，其目的是验证过程模型的正确性、提高过程模型的可靠性，进而提高软件质量.与非形式化的建模和验证相比，形式化的建模和验证更加准确，有利于计算机实现，是开发半自动化或自动化验证工具的基础.与软件过程建模相比，有关软件过程验证的研究相对较少.

针对软件演化过程建模，本文作者之一基于基本Petri网，扩展了面向对象技术和Hoare逻辑，提出了软件演化过程元模型EPMM(software evolution process meta model)，以及一系列建模方法、技术和工具，用以支持软件演化过程的建模［2］.EPMM的提出，有效解决了软件演化过程的形式建模问题.但是，软件演化过程模型被EPMM建模产生后，软件演化过程模型的形式验证问题却尚未得到解决.

对软件过程验证而言，一方面，目前相关文献主要集中在结构和性质层面，方法以语法检验和模型检测为主.结构验证是指检验过程模型的结构是否满足某些语法要求，只能从静态角度对软件过程模型的结构和语法进行检验，无法确保动态性质的满足;性质验证是指检验过程模型在执行过程中是否满足性质，无法确保过程模型的行为与过程规约一致.本文作者之一在文献［3］中对结构验证和性质验证的现状作了系统地总结.另一方面，现有的基于Petri网的过程模型验证方法可以大致分为4类［4］:①基于状态空间的验证方法，以Petri网模型检测方法为代表［5］;② 基于结构的验证方法;③ 基于逻辑推理的验证方法;④ 基于代数网的验证方法.但是，这些方法只能支持结构验证或性质验证，并不能很好地支持行为验证［4］.

针对当前软件过程缺乏行为验证的不足，文中引入ACP［6］风格的进程代数，对EPMM进行扩展，提出软件演化过程元模型代数EPMM-A(software evolution process meta model-algebra)，在其公理系统的支持下，基于等式推导验证软件演化过程模型的行为与行为规约是否一致，进而使得行为验证方式从模型推导变为代数推导.最后，通过证明EPMM-A公理系统的可靠性来说明代数推导方法的正确性.

文中首先提出拟解决的问题及其相关概念，然后讨论行为验证的方式，进而证明代数推导的正确性.

1 问题描述与相关概念

1.1 问题描述

形式验证软件演化过程模型的行为涉及3个问题:软件演化过程模型的形式化描述、行为规约的形式化描述和形式化的行为验证方式.

1.1.1 软件演化过程模型的形式描述

对于第1个问题，本文作者之一基于基本Petri网，扩展了面向对象技术和Hoare逻辑，提出了软件演化过程元模型EPMM.自上而下，EPMM分为4层:全局层、过程层、活动层和任务层.详细定义具体参见文献［2］.由EPMM的形式定义可知，由此建模产生的软件演化过程模型是形式化的.

例子过程工程师基于EPMM建模产生的软件演化过程模型p1，如图1所示.

本质上，由EPMM建模产生的软件演化过程模型是一个扩展的基本Petri网，条件集C中的元素只有“有托肯”和“无托肯”2种状态.

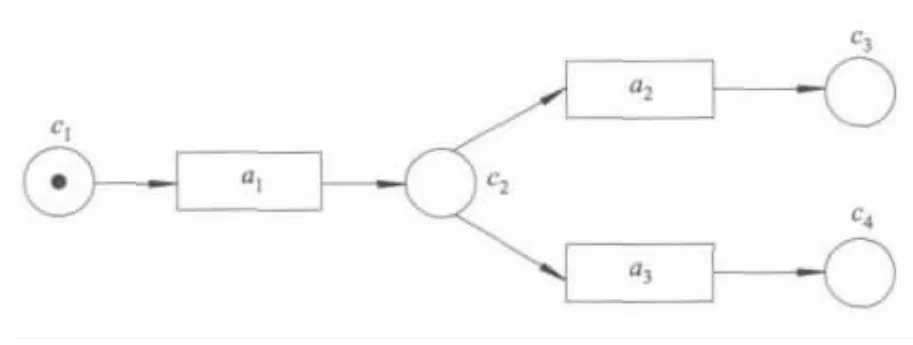
图1 一个软件演化过程模型p1

为了简便，这里忽略了全局层、活动层和任务层的形式定义，只给出了p1过程层的形式定义:

C={c1，c2，c3，c4};A={a1，a2，a3};F={(c1，a1)，(a1，c2)，(c2，a2)，(c2，a3)，(a2，c3)，(a3，c4)};M0={c1}，

式中:N={C，A;F}，称为p1的结构.

图形化的软件演化过程模型中的条件通常用圆圈表示，软件演化过程模型中的活动通常用方框表示.

1.1.2 行为规约的形式描述

对于第2个问题，本文作者之一使用ACP风格的进程代数对EPMM进行扩展，提出了软件演化过程元模型代数EPMM-A，既作为软件演化过程模型的代数语义域，又作为行为规约的形式规约语言.

EPMM-A包含3部分:第1部分是类子和常量，第2部分是操作符，第3部分是公理，具体参见表格1.其变迁规则规定了进程间的操作语义，参见表2.

表1 EPMM-A

关于EPMM-A的非形式化描述和变迁规则的非形式化描述，具体参见文献［3］.

定义1(行为规约) 行为规约是过程工程师根据过程需求，规定软件演化过程中活动的执行顺序.

例子假设软件演化过程开始执行活动a1，随后选择执行活动a2和a3，最后执行终止.根据过程需求，过程工程师使用EPMM-A，行为规约被描述为a1·(a2·δ+a3·δ).

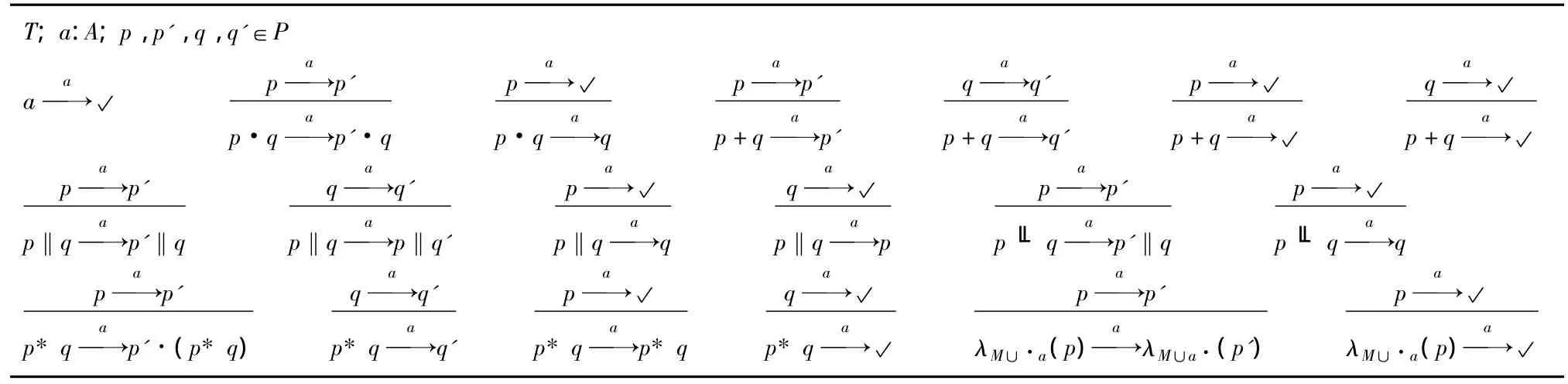
表2 EPMM-A的变迁规则

1.2 相关概念

为了从进程理论的角度对软件演化过程的行为进行研究，本节提出了行为空间、行为图和互模拟关系等基本概念.

定义2(变迁) 变迁是一个三元组b=(p，a，p')，形如pp'，其中，①p和p'表示进程，p，p'∈P，P是进程集;②a表示活动，a∈A，A是活动集.

变迁pp'表示进程p执行活动a后演化为进程p';变迁p表示进程p执行活动a后，能成功终止;变迁pδ表示进程p执行活动a后变为死进程.

需要注意的是，这里P是个抽象概念.在EPMM的上下文中，P指软件演化过程模型的集合;在EPMM-A中，P指进程项的集合.

为了以统一的方式比较进程间的行为，下面提出行为空间和行为图.

定义3(行为空间) 行为空间是一个二元组PBS=(P，B)，其中，①P是进程集;②B是变迁集.

定义4(行为图) 行为图是一个三元组BG=(P，E，R)，其中，①P是进程集;②E={(pi，pj)|pi，pj∈P，∃a∈A:(pi，a，pj)∈B}，其中，A是活动集，B是变迁集;③R:E→A，R(pi，pj)=a当且仅当(pi，a，pj)∈B;④ 选pi∈P作为顶点.称P中的元素为节点，E中的元素描述进程间的执行关系，R中的元素是进程执行的活动，pi为行为图的顶点.

互模拟关系是行为等价关系中最好的一种.所以，采用互模拟关系作为行为比较的一个标准.

定义5(互模拟关系) 互模拟关系R是直积P×P的子集当且仅当对于任意的p，p'，q，q'∈P和a

∈ 有:①;②;③ 其中，P是进程集，A是活动集.2个进程是互模拟的，记为p～q.

2 行为验证方式

仍给一个由EPMM建模产生的软件演化过程模型和一个基于EPMM-A定义的行为规约，如何判断软件演化过程模型的行为与行为规约定义的行为一致，这涉及验证方式.

文中行为验证的方式有两种:一种是人工推导的方式，称为模型推导，具体参见定义6;另一种是形式推导的方式，称为代数推导，具体参见定义7.

为了说明模型推导和代数推导的区别，下面将分别使用两种方式验证图1所示的P1是否满足行为规约a1·(a2·δ+a3·δ).

2.1 模型推导

定义6(模型推导) 判断一个由EPMM建模产生的软件演化过程模型的行为与一个基于EPMM-A定义的行为规约规定的行为是否等价，需要分别构建各自的行为图，找到互模拟关系，进行行为比较，这种行为验证方式称为模型推导.

使用模型推导验证p1是否满足行为规约a1·(a2·δ+a3·δ)，需要 3 步:

第1步，构建软件演化过程模型的行为图.根据Petri网的点火规则，p1的行为图如图2所示.其中，M0，M1，M2，M3是P1的情态，为M0={c1}，M1={c2}，M2={c3}，M3={c4};N是P1的结构，N={C，A;F}.

第2步，构建行为规约的行为图.根据EPMM-A的变迁规则，a1·(a2·δ+a3·δ)的行为图如图3所示.

第3步，判断软件演化过程模型和行为规约间是否存在互模拟关系.根据互模拟关系的定义，对基于p1的行为图和a1·(a2·δ+a3·δ)的行为图进行比较，不难发现，p1和a1·(a2·δ+a3·δ)间存在互模拟关系，如图4所示.

图4 p1和 a1·(a2·δ+a3·δ)间的互模拟关系

为了直观，图4中将存在互模拟关系的进程用虚线连接起来.不难证明:(N，M0)和a1·(a2·δ+a3·δ)、(N，M1)和 (a2·δ+a3·δ)、(N，M2)和 δ、(N，M3)和δ均是互模拟的.值得注意的是，p1在情态M2和M3处不能发生点火任何操作，则(N，M2)和(N，M3)代表死进程.

综上所述，软件演化过程模型p1与行为规约a1·(a2·δ+a3·δ)规定的行为等价.

从上述验证步骤可以看出，模型推导的过程需要分别构建软件演化过程模型和行为规约的行为图，并根据互模拟关系的定义，人工判断两者之间是否是互模拟的.

这种行为验证方式缺乏严格的形式化基础，具有相当的随意性，不利于开发计算机辅助验证工具.

2.2 代数推导

定义7(代数推导) 在EPMM-A的上下文中，基于公理系统，使用等式关系判断软件演化过程模型和行为规约是否等价，这种方式称为代数推导.

使用代数推导验证p1是否满足行为规约a1·(a2·δ+a3·δ)，需要2 步:

第1步，计算p1的代数语义.基于文献［3］提出的软件演化过程模型的代数语义，在行为等价的前提下，可以将待验证的软件演化过程模型p1形式转换为一个基于EPMM-A定义的进程项a1·(a2·δ+a3·δ).限于篇幅，具体计算过程参见文献［3］.

第2步，使用EPMM-A的公理系统，形式推导p1的代数语义和a1·(a2·δ+a3·δ)是否存在等式关系.若存在，则软件演化过程模型满足行为规约规定的行为.通过推导，不难发现，p1的代数语义a1·(a2·δ+a3·δ)和行为规约a1·(a2·δ+a3·δ)间存在等式关系.

综上所述，软件演化过程模型p1与行为规约a1·(a2·δ+a3·δ)规定的行为等价.

从上述验证步骤可以看出，代数推导的过程不需要构建软件演化过程模型和行为规约的行为图，也不需要人工判断两者间是否存在互模拟关系，只需计算软件演化过程模型的代数语义，并根据公理系统，形式推导软件演化过程模型的代数语义和行为规约间是否存在等式关系.

这种行为验证方式具有严格的形式化基础，支持形式验证，有利于开发计算机辅助验证工具.

3 代数推导的正确性

对软件演化过程模型的行为验证而言，为了说明代数推导的正确性，需要证明EPMM-A作为一个形式推理系统的可靠性.非形式化地说，可靠性是指在EPMM-A中，若存在进程项p和q，且p=q是由公理系统推导出的等式关系，则在进程项的行为空间中，p和q是互模拟的，即由公理系统形式推导出的互模拟关系一个也不会多，形式定义见定理4.

既然等式关系是由EPMM-A的公理系统通过替换性、等价性和同余性3种方式推导所得，从可靠性证明的角度，那么互模拟关系也应具有这3种性质.因此，文中首先证明互模拟关系具有等价性和同余性(congruence).

直观地说，等价关系是指如果p和q是互模拟的，则在EPMM-A的公理系统中，将p换成q后，不会改变系统的行为;同余关系是指多次应用EPMMA的公理系统中的公理将p转换成p'，将q转换成q'后，p'和q'也是互模拟的，参见定义9.

文中借鉴了通信与移动系统Pi演算中［7］进程上下文的定义，给出了代数项上下文的定义.非正式地说，一个进程项的上下文是包含一个洞的进程项表达式.

定义8(进程项的上下文) 一个进程项的上下文C由如下文法定义:

C::=［］|C+p|p+C|C·p|p·C|C‖p|p‖C|C╙p|p╙C|p*C|C*p，其中［］表示洞，p表示进程项.

C［q］表示将C中的洞里填入进程项q后得到的结果.

C::=［］|C+p|p+C|C·p|p·C|C‖p|p‖C|C╙p|p╙C|p*C|C*p称为进程项的上下文.

定义9(进程项上的同余关系) 令 Σ是EPMM-A上的基调，p，q和u是进程项，若进程项上的等价关系↔被进程项的上下文所保持，则称这个等价关系为进程项上的同余关系.

形式地说，等价关系↔被代数项的上下文所保持是指如果p↔q成立，则下列式子都成立:①p+u↔q+u;②u+p↔u+q;③pu↔qu;④up↔uq;⑤p‖u↔q‖u;⑥u‖p↔u‖q;⑦p╙u↔q╙u;⑧p*u↔q*u;⑨ λM(p)↔λM(q).

从定义9可知，同余关系必然是等价关系.

为证明进程项间的互模拟关系是同余关系，需引入两个概念:推导后的肯定变迁系统规约和组合格式.

3.1 推导后的肯定变迁系统规约

在并发交互式系统中，否定前提(参见定义10)的引入可以很好地解决死锁检测、优先级、随机行为和离散时间等问题.但是，否定前提的引入带来2个严重问题:①变迁规则不一致;② 变迁规则无法决定操作语义［8］.

定义10(肯定前提和否定前提) 若变迁规则的前提中包含否定变迁，则称前提为否定前提.若变迁规则的前提中不包含否定变迁，则称前提为肯定前提.

例如，一个变迁规则形如

由于前提中存在t!t'，所以此前提为负前提.由前提可知，代数项t不能执行活动a，演变为代数项t';由结论可知，代数项t执行活动a，演变为代数项t'.显然，前提和结论不一致，根据变迁规则无法判断变迁是否发生.

为了解决第1个问题，Groote在文献［8］中提出了一个方法用于检查变迁规则是否一致的问题.该方法基于逻辑编程(logic programming)中的分层法(stratification)，其基本思路:如果变迁规则的结论复杂性大于前提的复杂性，则此变迁规则是一致的.

为了解决第2个问题，Baeten在“带优先规则的项重写系统”中提出了三值稳定模型(three valued stable model)［9］，其基本思路:将变迁系统规约 TSS(由变迁规则组成)推导出的变迁分为彼此互不相交的3个集合:① 集合T表示可以发生的变迁集合;②集合F表示不可以发生的变迁集合;③集合U表示不确定是否可以发生的变迁集合.这样，一个变迁集合的划分可以由一个序偶＜T，U＞来决定，通过序偶＜T，U＞消除负前提带来的不确定性.

定义11(肯定变迁系统规约) 对于变迁系统规约TSS，若每个变迁规则的前提都不包含负变迁，则称TSS为肯定变迁系统规约.

由于肯定变迁系统规约不包含否定变迁，那么就不会出现变迁规则不一致的情形，因此也就不会出现无法判断变迁是否发生的情况.

定义12(推导后的肯定变迁系统规约)［8］若一个变迁系统规约TSS的最小三值稳定模型不包含不确定的变迁，则称变迁系统规约是推导后的肯定变迁系统规约.

定理1 EPMM-A的变迁系统规约是推导后的肯定变迁系统规约.

证明据表2可知，EPMM-A的每个变迁规则均不含有否定变迁，自然，EPMM-A的变迁系统规约必然是推导后的肯定变迁系统规约.

证毕.

综上所述，EPMM-A的变迁规则中由于不包含否定变迁，因此不必考虑负前提所带来的两个严重问题.

3.2 变迁规则的格式

自1981年Plotkin首次提出了结构化操作语义方法以来，使用Plotkin式的结构化方法定义进程代数、进程演算和规约语言的操作语义已经成为了一种事实上的标准.对于结构化操作语义，一个关键问题是:通过研究变迁规则的语法格式来确保互模拟关系是同余关系.

定义13(组合格式)［10］一个变迁规则ρ符合组合格式(panth format)，当满足以下3个条件:①对于ρ中的每个形如tt'的肯定前提，t'是单个变量;②对于ρ中的源只含有不超过一个的操作符;③在ρ的肯定前提的右边和ρ的源中都出现的相同变量，出现次数不能超过一次.

事实上，组合格式是ntyft/ntyxt格式［8］和path格式［10］的组合.它允许变迁和谓词同时存在，具有最大的语法自由性.

定理2 EPMM-A的变迁规则满足组合格式.

证明据表2可知，EPMM-A的每个变迁规则均满足定义13的3个条件，因此，EPMM-A的变迁规则满足组合格式.

证毕.

定理3 如果EPMM-A的变迁规则满足推导后的肯定变迁系统规约和组合格式，那么由变迁系统规约所推导出的进程项间的互模拟关系是同余关系，称为同余互模拟关系，记为.

证明设p，q，u是进程项;～是进程项上的互模拟关系.

先证互模拟关系是等价关系，再证其是同余关系.

1)证明互模拟关系是等价关系.根据互模拟关系的定义，p～p成立，即～是自反的，所以有:

若p～q成立，根据互模拟关系的定义，进程项p和q之间的行为可以相互模拟，那么q～p也成立，因此～是对称的.

若p～q和p～u成立，根据互模拟关系的定义，则有:进程项p和q之间的行为可以相互模拟，进程项q和u之间的行为也可以相互模拟，即p，q和u之间的行为都可以相互模拟，那么p～u成立，因此～是传递的.

综上所述，互模拟关系～是等价关系.

2)证明～是被进程项的上下文所保持.也就是说，如果p～q成立，则下列式子都成立:

①p+u↔q+u;②u+p↔u+q;③p·u↔q·u;④u·p↔u·q;⑤p‖u↔q‖u;⑥u‖p↔u‖q;⑦p╙u↔q╙u;⑧p*u↔q*u;⑨ λM(p)↔λM(q).

证明的详细过程，参见文献［6］.

综上所述，互模拟关系～是同余关系.证毕.

3.3 替换性的证明

证明了互模拟关系具有等价性和同余性后，对于可靠性的证明，还需要证明互模关系具有替换性，即证明:公理系统中的公理x=y(x和y代表变量，属于过程集P)，通过替换操作后，σ(x)和σ(y)是互模拟的.

定理4(可靠性) 如果EPMM-A┝p=q成立，则在进程项的行为空间中╞p～q成立，其中┝代表形式推导，╞代表逻辑蕴含.

证明为了证明简便，令σ(x)=a，σ(y)=b，σ(z)=c，其中a，b，c∈T(Σ).

1)在EPMM-A中，对于公理A1-A7而言，可靠性的证明过程如下:

公理A1:x+y=y+x描述了选择复合操作符具有交换性.通过替换操作，2个进程项的行为图如图5所示.

图5 2个进程项的行为图

由图5可以找出进程项间存在的互模拟关系:a+b～b+a，b～b，a～a.因此，进程项a+b和b+a是互模拟的.

公理A2:(x+y)+z=x+(y+z)描述了选择复合操作符具有结合性，采用上述方法，不难证明(x+y)+z=x+(y+z)是互模拟的.

公理A3:x+x=x描述了变量x和x之间的选择复合等价于x本身，采用上述方法，不难证明x+x和x是互模拟的.

公理A4:(x+y)·z=x·z+y·z描述了选择复合操作符对于顺序复合操作符满足分配律，采用上述方法，不难证明(x+y)·z和x·z+y·z是互模拟的.

公理A5:(x·y)·z=x·(y·z)描述了顺序复合操作符具有结合性，采用上述方法，不难证明(x·y)·z=x·(y·z)是互模拟的.

公理A6:x+δ=x描述了变量x和死进程δ之间的选择关系，采用上述方法，不难证明x+δ和x是互模拟的.

公理A7:δ·x=δ描述了变量x和死进程δ之间的顺序关系，采用上述方法，不难证明δ·x和δ是互模拟的.

2)在EPMM-A中，对于公理S1和S2而言，可靠性的证明过程如下:

公理S2:(t1|t2)|t3=t1|(t2|t3)描述了任务间的同步操作具有结合性.从执行效果看，(t1|t2)|t3和t1|(t2|t3)均表示活动a，因此两者是互模拟的.

3)在EPMM-A中，对于公理M1-M4而言，可靠性的证明过程如下:

公理M1:x‖y=x╙y+y╙x定义了并发复合操作的内涵.EPMM-A支持交叠式语义，并发复合操作可以简化为左并发复合操作符.在交织式语义的上下文中，从观察者的角度，x‖y和x╙y+y╙x的执行效果是等价的，因此两者是互模拟的.

公理M2:a╙x=a·x定义了左并发复合操作符的内涵.在交织式语义的上下文中，从观察者的角度，a╙x和a·x的执行效果是等价的，因此两者是互模拟的.

公理M3:a·x╙y=a·(x‖y)也定义了左并发复合操作符的内涵.在交织式语义的上下文中，从观察者的角度，a·x╙y和a·(x‖y)的执行效果是等价的，因此两者是互模拟的.

公理M4:(x+y)╙z=x╙z+y╙z描述了左并发复合操作符对选择复合操作符具有右分配性.采用上述方法，不难证明(x+y)╙z和x╙z+y╙z x是互模拟的.

4)在EPMM-A中，对于公理C1-C3而言，可靠性的证明过程如下:

公理C1:x‖y=y‖x描述了并发复合操作符具有交换性.采用上述方法，不难证明x‖y和y‖x是互模拟的.

公理C2:(x‖y)‖z=x‖(y‖z)描述了并发副恶化操作符具有结合性.采用上述方法，不难证明(x‖y)‖z和x‖(y‖z)是互模拟的.

公理C3:(x╙y)╙z=x╙(y‖z)描述了左并发复合操作符和并发复合操作符之间的关系.采用上述方法，不难证明(x╙y)╙z和x╙ (y‖z)是互模拟的.

5)在EPMM-A中，对于公理CSO1-CSO5而言，可靠性的证明过程如下:

公理CSO1:λM(δ)=δ描述了死进程不能发生任何点火操作.从观察者的角度，λM(δ)和δ都不能执行任何活动，两者是互模拟的.

公理CSO2:·a⊆M∧a·∩M=⇒λM(a)=a定义了状态操作符的内涵.若活动a在情态M处是使能的，则λM(a)=a，那么，λM(a)和a是互模拟的.

公理CSO3:·a!⊆M∧a·∩M≠⇒λM(a)=δ定义了状态操作符的内涵.同上，两者也是互模拟的.

公理 CSO4:λM(x+y)=λM(x)+λM(y)描述了状态操作符对选择复合操作符具有左分配律.通过替换操作，2个进程项为λM(a+b)和λM(a)+λM(b)，分4种情况进行讨论:若活动a在情态M处是使能的，则 λM(a+b)=a，λM(a)+λM(b)=a+δ=a，因此，λM(a+b)=a和 λM(a)+λM(b)是互模拟的;若活动b在情态M处是使能的，则λM(a+b)=b，λM(a)+λM(b)=δ+b=b，因此，λM(a+b)=a和λM(a)+λM(b)是互模拟的;若活动a和b在情态M处不是使能的，则 λM(a+b)=δ，λM(a)+λM(b)=δ，因此，λM(a+b)=a和 λM(a)+λM(b)是互模拟的;若活动a和b在情态M处都是使能的，则 λM(a+b)=a+b，λM(a)+ λM(b)=a+b，因此，λM(a+b)=a和λM(a)+λM(b)是互模拟的.综上所述，λM(x+y)和λM(x)+λM(y)是互模拟的.

公理 CSO5:λM(a·x)= λM(a)·(x)定义了状态操作符的内涵.采用上述方法，不难证明 λM(a·x)和 λM(a)·λ(x)是互模拟的.

6)在 EPMM-A中，对于公理 BKS1、BKS2和BKS3的可靠性证明过程，请参看文献［6］.

证毕.

4 结论

1)使用ACP对EPMM进行扩展，提出了软件演化过程元模型代数EPMM-A.

2)使用EPMM-A形式定义软件演化过程模型的行为规约.

3)基于文献［3］提出的代数语义，在EPMM-A公理系统的支持下，使用等式推导验证软件演化过程模型的行为与行为规约是否一致，进而使得行为验证方式从模型推导(非形式化)变为代数推导(形式化).

4)为了说明代数推导的正确性，证明了软件演化过程元模型代数作为一个形式推理系统的可靠性.

References)

［1］李明树，杨秋松，翟健.软件过程建模方法研究［J］.软件学报，2009，20(3):524-545.Li Mingshu，Yang Qiusong，Zhai Jian.Systematic review of software process modeling and analysis［J］.Journal of Software，2009，20(3):524-545.(in Chinese)

［2］ Li T.An Approach to Modelling Software Evolution Processes［M］.Berlin:Springer-Verlag，2008.

［3］代飞，李彤，谢仲文，等.一种软件演化过程模型的代数语义［J］.软件学报，2012，23(4):846-863.Dai Fei，Li Tong，Xie Zhongwen，et al.Towards an algebraic semantics of software evolution process models［J］.Journal of Software，2012，23(4):846-863.(in Chinese)

［4］代飞.基于EPMM的软件演化过程模型验证［D］.昆明:云南大学软件学院，2011.

［5］段振华，张曼.Petri网模型检测概述［J］.中国计算机学会通讯，2009，5(10):21-28.Duan Zhenhua，Zhang Man.Detection survey of Petri net model［J］.Communications of the CCF，2009，5(10):21-28.(in Chinese)

［6］ Fokkink W.Introduction to Process Algebra［M］.Berlin:Springer-Verlag，2007.

［7］ Robin Milner.通信与移动系统π演算［M］.北京:清华大学出版社，2009.

［8］ Groote J F.Transition system specifications with negative premises［J］.Theoretical Computer Science，1993，118(2):263-299.

［9］ Baeten JCM，Bergstra JA，Klop JW，et al.Term-rewriting systems with rule priorities［J］.Theoretical Computer Science，1989，67(2/3):283-301.

［10］ Baeten J C M，Verhoef C.A congruence theorem for structured operational semantics with predicates［C］∥Proceedings of CONCUR93，LNCS715.Berlin:Springer-Verlag，1993:477-492.