一种改进的LLL模糊度规约算法

吕 浩，吕志平，翟树峰，邝英才，王福林

（1.信息工程大学 地理空间信息学院，郑州 450000；2.61287部队，昆明 650000）

一种改进的LLL模糊度规约算法

吕 浩1，吕志平1，翟树峰1，邝英才1，王福林2

（1.信息工程大学 地理空间信息学院，郑州 450000；2.61287部队，昆明 650000）

整周模糊度的高效解算是GNSS高精度数据处理中的关键，基于格论进行GNSS模糊度估计时需要通过格基规约来实现最优整周模糊度向量的快速搜索。针对高维情况下常规LLL规约算法辅助整周模糊度解算存在规约耗时较长和规约性能有限的问题，引入最小列旋转QR分解技术对基向量进行预排序，采用延后尺度规约和部分尺度规约来减少规约过程中的冗余尺度规约，以改善LLL算法的执行效果。分别通过模拟和实测数据进行实验，结果表明：改进后的LLL算法可以明显降低格基规约耗时，实测环境下其规约效率相比于传统方法提高了约 10倍，且能够保证较好的规约性能，从而有效提升高维模糊度的解算效率。

模糊度解算；格基规约；LLL规约；QR分解；尺度规约

在GNSS精密定位数据处理中，相位整周模糊度的快速、精确解算是保证定位精度和可靠性的关键，也是GNSS研究领域中的热点问题和难点问题。在众多的模糊度解算方法中，基于模糊度域内的LAMBDA算法应用最为广泛[1]，该方法以整数最小二乘原理为基础，通过降低模糊度方差分量间的相关性来压缩搜索空间，提高搜索效率。随后，针对模糊度降相关问题的多种方法被相继提出[2-5]。

模糊度解算作为一个整数最小二乘问题，实际上等价于格理论中的最近向量问题（CVP）[6-7]。由于格的特殊性质，为保证高效、精确地求解CVP，首先要对格基进行规约处理，其中以LLL规约算法最为流行[8-9]。文献[10]最早将格基规约的思想引入到 GNSS整周模糊度解算当中；文献[11]从理论上证明了 LLL规约算法和LAMBDA降相关之间的等价性；文献[12]指出单纯的尺度规约过程对搜索空间和搜索效率没有影响，并提出了部分尺度规约；文献[13]通过改变尺度规约顺序来降低LLL算法计算复杂度；文献[14-15]分别采用最小列旋转技术和贪心算法来减少规约过程中的基向量交换次数。近来的研究进一步指出，为提高模糊度搜索效率，格基规约的本质在于尽可能促使基向量按照一定方向排序[16-17]。已有的格基规约算法主要是围绕基向量交换条件和尺度规约的有效性来寻求单一的规约计算复杂度的降低或规约性能的改善，而提高规约性能往往会导致计算复杂度的增大，因此需要对两者进行平衡来减少整体解算耗时。

在解决高维模糊度参数时，由于规约耗时通常远大于搜索耗时，因而减少规约耗时对于提高模糊度整体解算效率影响显著。鉴于此，本文在分析LLL规约算法的基础上，对该算法进行优化改进，在降低规约复杂度的同时兼顾规约性能，并结合模拟和实测数据进行了验证与分析。

1 基本数学模型

1.1 基于格的模糊度估计

基于载波相位测量的GNSS定位模型是一种混合整数模型，通过经典最小二乘可以得到模糊度的实数解及其方差协方差阵Qˆa。考虑模糊度的整数约束，则对应的整数最小二乘的估计准则为：

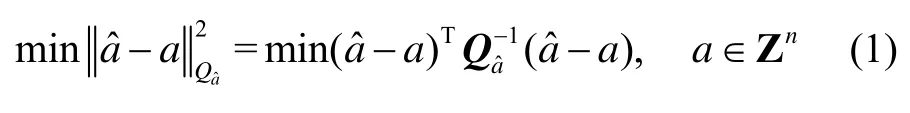
对Qˆa进行Cholesky分解：

其中，B为上三角矩阵。则式(1)可以表示为：

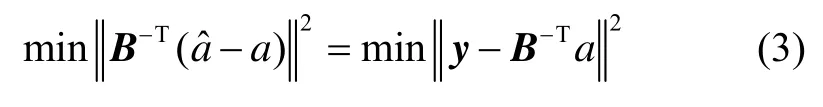
式中，y=B-T为常量。该式在格理论中被称为最近向量问题，B为基于Qˆa获得的格基。

于是，模糊度解算过程即可转化为求解与目标向量y最近的格上向量，常采用LLL规约算法来处理此类问题。

1.2 LLL格基规约

采用经典 LLL规约算法对上述问题进行处理时还需要对基矩阵B进行分解：

若矩阵B*和U中的元素满足以下条件[8]：

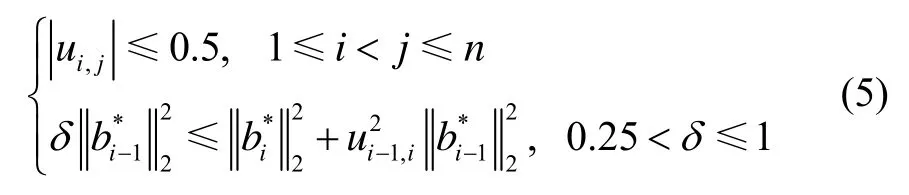
则称B为LLL规约基，其中第一项称为尺度规约，第二项称为基向量交换。

在实际解算中，为了保证较好的数值稳定性，常基于QR分解来实现LLL规约[18-19]。令基矩阵B=QR，其中，Q为正交矩阵，R为上三角矩阵，且对角线元素则有：

于是，LLL算法的规约条件可以改写为：

为了满足上述规约条件，通常需要构造变换矩阵进行规约操作。

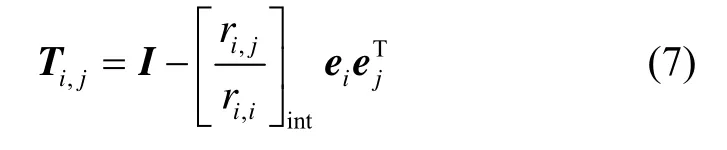
式中，[ ]int为取整操作，利用其右乘基矩阵B即可实现对应元素的尺度规约，同时更新上三角矩阵R。

2）基向量交换（Swap变换）：若不满足式(6)中条件2的要求，即时，则构造初等变换矩阵来调换的顺序，并对上三角矩阵R进行更新。

基于QR分解的LLL规约同经典LLL规约本质上是相同的，但仅基于上三角阵进行变换操作，较为简便，且拥有更高的浮点精度。

2 LLL改进算法

根据LLL规约算法定义可知，其主要由尺度规约和基向量交换两部分构成，其中：尺度规约对模糊度搜索效率并无直接影响[14]，而是为了促使基向量得以充分交换；LLL规约的核心正是通过基向量交换来实现模糊度快速搜索。因此，本文基于规约效率和规约性能的平衡这一目的，对LLL算法进行改进。

2.1 延后尺度规约与部分尺度规约

在引入新的尺度规约手段之前，首先对常规LLL算法中尺度规约的特点和有效性进行分析。将LLL算法中的尺度规约分为两类：第一类是次对角线元素的尺度规约；第二类是当基向量交换条件（Swap条件）不满足时，对列向量中其余元素进行尺度规约。这两类尺度规约的计算过程如图1所示。

图1 LLL算法尺度规约过程Fig.1 Process of LLL size reduction

由图1可知，LLL算法中尺度规约的执行是根据是否满足Swap条件，在第k层、第max(k-1, 2)层和第k+1层三个规约层之间循环往复，因而相同的规约层由于基向量交换的影响，必然会导致部分第一类尺度规约和第二类尺度规约的重复执行。

1）延后尺度规约

根据LLL算法尺度规约的特点，由于同一规约层存在重复规约，所以只有当规约后能够进行基向量交换时，第一类规约才是必需的；除此以外的第一类和第二类规约均可在规约基B完成所有基向量交换后再执行。

将第一类尺度规约和基向量交换步骤进行合并，此时的基向量交换条件如下：

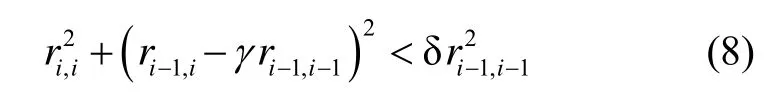
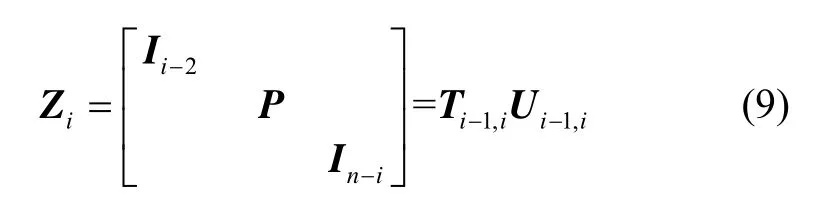
其中2维矩阵P表示如下：

利用变换矩阵Zi对格基B和上三角矩阵R进行更新，用Zi右乘R，同时消去R的对角线以下元素。

该过程即为规约后基向量交换，在对B完成所有上述操作后可以将剩余的第一类和第二类尺度规约延迟到算法最后执行。需要说明的是，延后尺度规约仅消除LLL算法中基向量交换引起的冗余尺度规约，不改变基向量交换策略。

2）部分尺度规约

对于常规LLL算法，文献[12]从几何角度说明了尺度规约不改变规约基的施密特正交化向量长度，因而其对于搜索效率并不构成影响。考虑到基向量交换对搜索效率改善的作用，一般仅对次对角线元素进行尺度规约，亦即第一类尺度规约；但为了保证算法的有效性和稳定性，还需要有选择性地进行第二类尺度规约。

在延后尺度规约中，不影响基向量交换的第一类和第二类尺度规约被置于算法最后一步。因此，采用部分尺度规约，对于其中的第二类尺度规约只在满足一定条件下进行。

部分尺度规约针对的是第二类尺度规约，为避免出现数值稳定性问题而选择部分执行，在不影响基向量交换的基础上进一步减少了LLL算法的尺度规约数。

2.2 最小列旋转QR分解

已有的研究表明，格基规约的目的是为了使基向量按照特定方向排序[17]。除了尺度规约的个数，基向量交换的次数也会对格基规约的效率产生影响，且基向量的排序直接影响到规约基性能的好坏。因此，考虑在正式的格基规约前可以按照某种准则对规约基向量进行预排序，进而减少规约过程中的基向量交换。

通常基于Householder变换实现QR分解，假设对格基B的前i-1个向量进行 Householder变换后得到的矩阵为Ri-1。最小列旋转QR分解是指在对格基B进行第i步 QR分解之前，找到对应当前子矩阵中列向量长度最小的那一列并构造初等变换矩阵Ui交换Ri-1的第i列和第j列；然后再构造Householder变换矩阵Hi进行常规的第i步 QR分解，实现矩阵的上三角化最小列旋转QR分解的整体变换过程可以表示为：

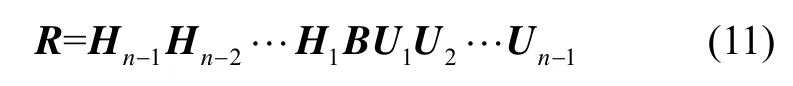
显然，在第i步最小列旋转QR分解完成后，R中的元素满足如下条件：

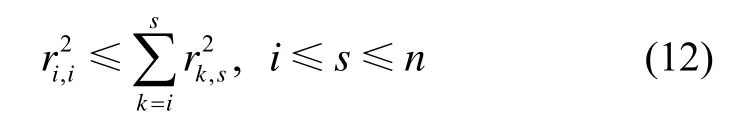
根据Householder变换的性质，对矩阵Ri-1Ui进行上三角化并不改变矩阵列向量长度。式(12)表明，通过以上策略能够保证每一步变换后得到的对角线元素ri,i小于子矩阵中其它列向量长度。

2.3 算法流程

将上述基于LLL算法的改进策略进行整合，主要从尺度规约和基向量交换两个方面对算法进行优化处理，具体流程见图2。

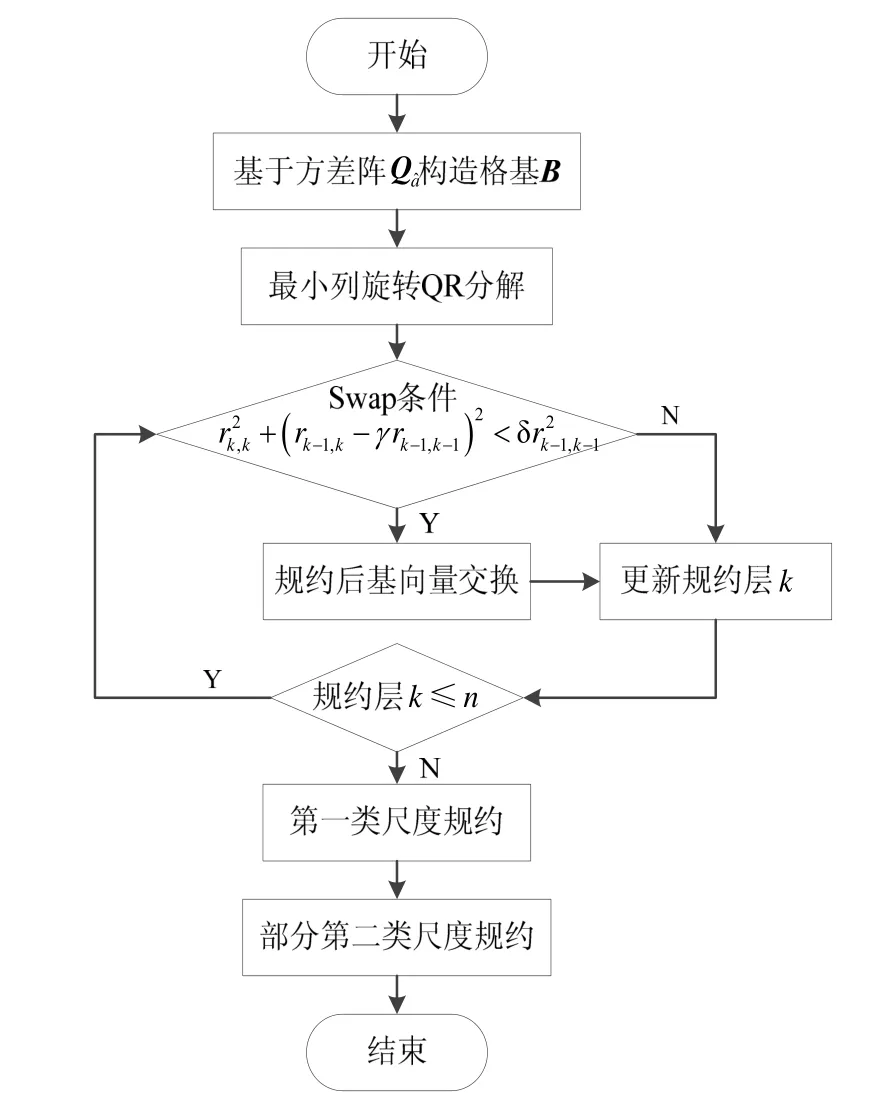
图2 LLL改进算法流程图Fig.2 Flow chart of modified LLL algorithm

如图2所示，改进后算法的处理步骤主要包括：基于模糊度方差协方差阵Qˆa构造格基B，对原始格基进行最小列旋转QR分解得到上三角阵R；设定初始的规约层k，根据式(8)的基向量交换条件进行判断，如果成立则进行规约后基向量交换，即对应式(9)的第一类尺度规约与基向量交换的合并操作，并更新规约层否则直接进入规约层k=k+1；若规约层k≤n，则重复上步操作直到循环结束；最后在第一类尺度规约的基础上，根据当前次对角元素是否满足进行部分第二类尺度规约。

3 算例分析

文献[7]提出的基于Householder变换的LLL规约（HLLL规约）其实就是基于QR分解的LLL规约；文献[20]提出的 HELLL规约算法实际上是基于最小列旋转和全部尺度规约的迭代操作。本文将基于延后尺度规约技术和QR分解的LLL规约称为DLLL算法，将图2中对应的LLL改进算法称为DPLLL算法。

为了评估 LLL改进算法在模糊度解算中的应用效果，分别基于模拟和实测数据结合不同指标对LLL、HLLL、DLLL、HELLL和DPLLL算法进行验证比较和统计分析。在模糊度解算过程中，模糊度的搜索部分统一采用目前广泛应用的SE-VB算法[5]。实验环境为：华硕PC机（Intel Core i7-6700 CPU，2.60GHz，内存 8.0GB，64位 Windows10 操作系统），软件MATLAB R2014a（8.3.0.532）。

3.1 实验1

利用文献[2]的随机模拟方法构建模糊度协方差阵，具体构造如下：

式中：U为单位正交矩阵，通过 Givens旋转原理进行构造；Λ为对角阵，其元素为矩阵Qˆa的特征值的升序排列。当Qˆa的维数大于20时，条件数对数值取值范围为[3, 4.5]；低维情况下条件数对数值取值范围为[0, 4.5]。条件数按照均匀分布在取值范围内随机产生，特征值也按照均匀分布随机产生，且最大值λmax与最小值λmin满足与条件数c的关系：在实验1中，本文分两组方案进行模拟数据实验。

1）第一组模拟实验

由式(13)生成10、20、30、40维的仿真数据，每一维构造100组数据，分别采用LLL、HLLL和DLLL算法对每一维数据进行模糊度规约处理，并计算 100组数据的平均尺度规约个数和平均规约耗时，结果如表1所示。由表1可以看出，随着维数的增加，模糊度规约过程中的尺度规约个数和规约耗时均逐渐增加，HLLL与LLL相比仅基于上三角阵操作，其规约耗时更少但尺度规约数不变，而DLLL在HLLL基础上引入延后尺度规约技术，其规约耗时和尺度规约数均明显小于 HLLL。此外，三种规约算法的基向量交换部分的步骤相同，因而其处理后的规约基是一致的。

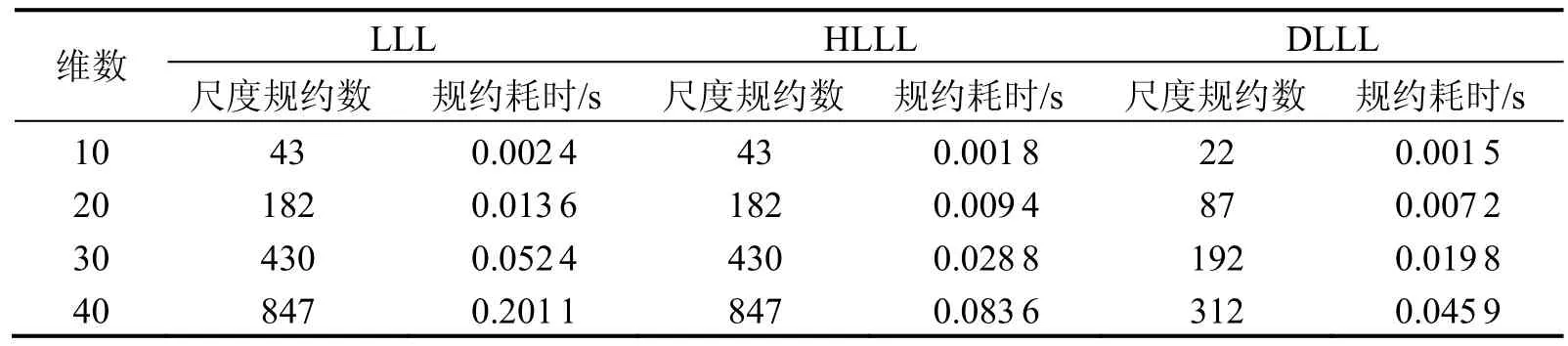
表1 不同维数下的尺度规约数和规约耗时Tab.1 Numbers of size reduction and the reduction time in different dimensions

2）第二组模拟实验

利用随机模拟方法构建 3～40维的模糊度方差协方差阵，同样每一维构造100组数据，分别采用HLLL、HELLL和DPLLL算法对其进行规约处理。图3(a)和图3(b)分别为三种算法对应100组数据的平均尺度规约数和平均基向量交换数随不同维数的变化趋势。图4为对应不同维数下的平均规约耗时的情况。

图3 不同维数下的尺度规约数和基向量交换数Fig.3 Numbers of size reduction and base vectors swapping in different dimensions

从图3中可以看出，三种算法的尺度规约数和基向量交换数均与维数成正相关关系，即随着维数的增大而呈整体上升趋势，其中改进后的 DPLLL规约算法拥有最少的尺度规约数和基向量交换数，且明显小于HLLL和HELLL算法。

从图4中可以看出，三种算法的规约耗时均随着维数的增加而变大，其中：HELLL在低维（10维以下）可能存在耗时大于HLLL的情况，随着维数增加HELLL规约时间要小于HLLL算法；而DPLLL则由于大大减少了尺度规约和基向量交换的操作次数，所需要的规约耗时最少。

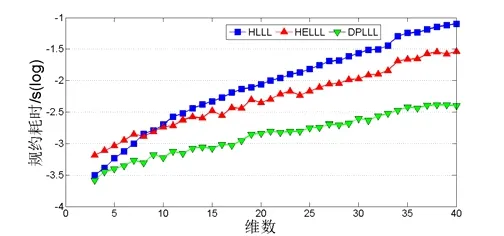
图4 不同维数下的规约耗时Fig.4 Reduction time in different dimensions

3.2 实验2

为进一步验证改进后算法的有效性，采用HLLL、HELLL和DPLLL算法基于实测GNSS数据进行实验。实验选取基线长约为10.5 km的GPS+BeiDou双频数据单历元处理后的模糊度及其方差协方差阵，接收机型号为Trimble NETR9，采样间隔为30 s，历元数为200，模糊度维数均在30维以上。

图5为三种规约算法200个历元下的规约耗时情况，从图中可以看出，DPLLL算法的规约耗时最小，而HELLL与HLLL算法的规约时间在实测环境下无明显大小差异规律，这可能与HELLL算法迭代操作过程有关，其中DPLLL算法的平均规约耗时仅为传统算法的1/10。

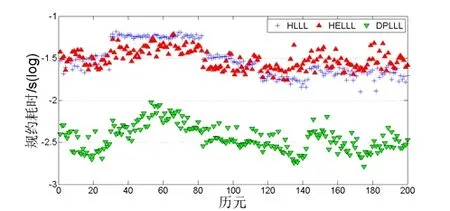
图5 不同历元下的规约耗时Fig.5 Reduction time in different epochs

进一步地，鉴于格基规约的本质在于促使基向量按特定方向排序，以规约得到的规约基的施密特正交化向量长度排列趋势来衡量不同规约算法的性能[7]，如图6所示。从图6中可以看出：HLLL算法规约后的正交化向量长度排列抖动较大；DPLLL算法由于采用最小列旋转QR分解进行预排序，其排列趋势明显改善；而HELLL算法通过迭代处理可获得满足式(12)的更强的规约基，其正交化向量长度排列最为平缓，从而说明其规约后的性能要优于HLLL和DPLLL算法。这里 HELLL算法可获得性能最优的规约基，但由图4和图5可知，相比于DPLLL算法，HELLL算法并不能有效提高规约效率。

图6 单历元规约后正交化向量长度变化趋势Fig.6 Trend of the length of orthogonal vectors after reduction in single epoch

图7(a)和图7(b)分别对应三种算法不同历元下的搜索耗时和模糊度整体解算耗时。由图 7(a)可知，HELLL算法的搜索耗时小于其他两种算法，这与图6的分析是一致的，即HELLL算法获得的规约基性能最优，DPLLL算法次之。但在高维模糊度解算中，搜索耗时占模糊度整体解算耗时的比例很小，减少模糊度整体解算耗时的关键在于提高规约效率，而不是单一地追求性能最优，因此考虑结合规约耗时来比较三种算法对模糊度解算效果的影响。根据图7(b)可以发现，同时顾及模糊度规约和搜索过程时，本文提出的DPLLL算法的整体解算耗时最小，即模糊度处理整体效率最高。

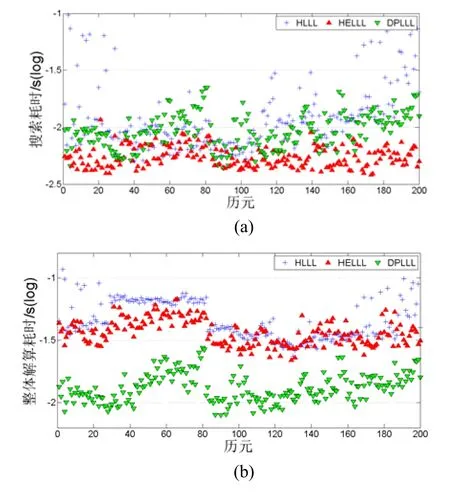
图7 不同历元下的搜索耗时和整体解算耗时Fig.7 Search time and entire computation time in different epochs

4 结 论

本文在分析 LLL规约算法的流程和特点的基础上，通过引入最小列旋转QR分解、延后尺度规约和部分尺度规约技术对常规LLL算法进行改进，提出了DPLLL规约算法，并基于仿真和实测数据进行了验证分析。从实验结果可以看出，改进后的算法可以有效减少格基规约过程中的尺度规约数和基向量交换数，并且能够获得较好的规约性能，显著改善了LLL算法的规约效果。利用 DPLLL算法处理的规约效率和模糊度整体解算效率都得到了明显提高，从而有利于模糊度解算的快速实现。同时，随着组合系统定位和观测频率的增加，如何更好地平衡高维模糊度解算过程中的规约效率和规约性能将是下一步研究的重点。

（References）：

[1]Li B, Verhagen S, Teunissen P J G.GNSS integer ambiguity estimation and evaluation: LAMBDA and Ps-LAMBDA[C]//Proceedings of China Satellite Navigation Conference.Wuhan, 2013: 291-301.

[2]Xu P L.Random simulation and GPS decorrelation[J].Journal of Geodesy, 2001, 75: 408-423.

[3]Chang X, Yang X, Zhou T.MLAMBDA: a modified LAMBDA method for integer least-squares estimation[J].Journal of Geodesy, 2005, 79(9): 552-565.

[4]Xu P L.Parallel cholesky-based reduction for the weighted integer least squares problem[J].Journal of Geodesy,2012, 86(1): 35-52.

[5]李豹, 许江宁, 曹可劲, 等.改进 LAMBDA 算法实现单频GPS 整周模糊度快速解算[J].中国惯性技术学报,2013, 21(3): 365-368.Li B, Xu J N, Cao K J, et al.Fast resolution of single frequency GPS integer ambiguity realized by improved LAMBDA algorithm[J].Journal of Chinese Inertial Technology, 2013, 21(3): 365-368.

[6]刘经南, 于兴旺, 张小红.基于格论的GNSS模糊度解算[J].测绘学报, 2012, 41(5): 636-645.Liu J N, Yu X W, Zhang X H.GNSS ambiguity resolution using lattice theory[J].Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 636-645.

[7]范龙.基于格理论的 GNSS模糊度估计方法研究[D].郑州: 信息工程大学, 2013.Fan L.Research on method of integer ambiguity estimation with lattice theory[D].Zhengzhou: Information Engineering University, 2013.

[8]Aliev I, Henk M.LLL-reduction for integer knapsacks[J].Journal of Combinatorial Optimization, 2012, 24(4): 613-626.

[9]Neumaier A, Stehle D.Faster LLL-type reduction of lattice bases[C]//Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation.Canada, 2016: 373-380.

[10]Hassibi A, Boyed S.Integer parameter estimation in linear models with applications to GPS[J].IEEE Transactions on Signal Processing, 1998, 46(11): 2938-2952.

[11]Lannes A.On the theoretical link between LLL-reduction and Lambda-decorrelation[J].Journal of Geodesy, 2013,87(4): 323-335.

[12]Cong L, Howgrave-graham N.Effective LLL reduction for lattice decoding[C]//IEEE International Symposium on Information Theory.Nice, France, 2007: 196-200.

[13]Luo Y X, Qiao S Z.A parallel LLL algorithm[C]//Proceedings of the Fourth International C* Conference on Computer Science and Software Engineering.Montreal.Quebec, Canada, 2011: 93-101.

[14]Xie X, Chang X W.Borno M A.Partial LLL reduction[C]//Proceeding of IEEE GLOBECOM.Houston, USA, 2011.

[15]卢立果, 刘万科, 李江卫.一种有效的LLL规约算法[J].武汉大学学报(信息科学版), 2016, 41(8):1118-1124.Lu L, Liu W K, Li J W.An effective LLL reduction algorithm[J].Geomatics and Information Science of Wuhan University, 2016, 41(8): 1118-1124.

[16]Borno M A, Chang X W, Xie X H.On decorrelation in solving integer least-squares for ambiguity determination[J].Survey Review, 2014, 46: 37-49.

[17]卢立果，刘万科，李江卫.降相关对模糊度解算中搜索效率的影响分析[J].测绘学报2015, 44(5)：481-487.Lu L G, Liu W K, Li J W.Impact of decorrelation on search efficiency of ambiguity resolution[J].Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 481-487.

[18]卢立果.基于球形搜索的模糊度格基规约方法研究与分析[D].武汉: 武汉大学, 2013.Lu L G.The research and analysis based on sphere search for ambiguity on reduction[D].Wuhan: Wuhan University,2013.

[19]Jazaerl S, Amiri-Simkooei A R, Sharifi M A.Fast integer least-squares estimation for GNSS high-dimensional ambiguity resolution using lattice theory[J].Journal of Geodesy,2012, 86: 123-136.

[20]谢恺, 柴洪洲, 范龙, 等.一种改进的LLL模糊度降相关算法[J].武汉大学学报(信息科学版), 2014, 39(11):1363-1368.Xie K, Chai H Z, Fan L, et al.An improved LLL ambiguity decorrelation algorithm[J].Geomatics and Information Science of Wuhan University, 2014, 39(11): 1363-1368.

[21]Wu M K, He J, Wang H C.Reliable single epoch ambiguity resolution for precise attitude determination using BeiDou triple-frequency observations[J].Journal of Chinese Inertial Technology, 2016, 24(5): 624-631.

Improved LLL ambiguity reduction algorithm

LYU Hao1, LYU Zhi-ping1, ZHAI Shu-feng1, KUANG Ying-cai1, WANG Fu-lin2
(1.Institute of Geography and Spatial Information, Information Engineering University,Zhengzhou 450000, China; 2.Unit 61287 of PLA, Kunming 650000, China)

Efficient ambiguity resolution is the key of GNSS data processing with high precision.Based on the lattice theory, the computational efficiency of searching the optimal integer ambiguity vector can be improved by using lattice reduction.According to the fact that the routine LLL reduction algorithm for ambiguity resolution under high-dimensional case has long reduction time and limited reduction performance, the QR factorization with minimum column pivoting was introduced to preorder the reduction base vectors, and the algorithms of delayed size reduction and partial size reduction were used to reduce the number of redundant size reduction.These methods were optimally combined to improve the implementation effects of LLL reduction algorithm.Experiments with simulated and real GNSS data were executed,respectively.The consequence shows that the modified LLL algorithm can effectively reduce the reduction time and provide better performance than those of current reduction methods.The computing efficiency of lattice reduction using the proposed method with real data is improved by nearly 10 times than those of traditional algorithms.Therefore the computational efficiency of ambiguity resolution under high-dimensional case can be improved significantly by using the proposed algorithm.

ambiguity resolution; lattice reduction; LLL reduction; QR decomposition; size reduction

P228.1

A

1005-6734(2017)05-0611-07

10.13695/j.cnki.12-1222/o3.2017.05.010

2017-07-25；

2017-09-10

国家自然科学基金（41674019）；国家重点研发计划（2016YFB0501701）

吕浩（1989—），男，博士研究生，从事测量数据处理理论与方法研究。E-mail: lyangeo@126.com