基于浸入与不变原理的四旋翼姿态系统反步滑模控制

夏琳琳，丛靖宇，马文杰，赵 耀，刘惠敏

（1.东北电力大学 自动化工程学院，吉林 132012；2.东北电力大学 理学院，吉林 132012；3.青岛农业大学 机电工程学院，青岛 266109）

基于浸入与不变原理的四旋翼姿态系统反步滑模控制

夏琳琳1，丛靖宇1，马文杰2，赵 耀1，刘惠敏3

（1.东北电力大学 自动化工程学院，吉林 132012；2.东北电力大学 理学院，吉林 132012；3.青岛农业大学 机电工程学院，青岛 266109）

针对较大幅度外部不确定扰动下的四旋翼姿态稳定问题，设计了一种基于浸入与不变原理（I&I）的自适应反步滑模控制器（ABSMC）。首先建立了未知大扰动下四旋翼姿态系统动力学模型，然后以横滚角子系统搭建为例，设计并应用了反步法和基于趋进率的滑模控制策略。在扰动估计误差流型设计中，融合了I&I原理，即自适应率的选取实现了误差流型的不变和吸引，确保估计误差收敛到0。最后，对系统进行了稳定性分析和数字仿真。结果表明，在较大未知扰动情况下，融合I&I原理方法后，经10 s所测跟踪误差平方的累加和仅为传统ABSMC方法的11.2%，控制精度大幅提高。

四旋翼；姿态系统；浸入与不变原理；反步法；滑模控制

四旋翼飞行器的动力学模型具有非线性、强耦合、高阶数等特点[1]。得益于自身可垂直起降、可悬停等灵活机动的特性，广泛应用于近地环境下的航拍、刑侦、风力发电设备检修、环境监控及交通管理等领域。在多旋翼无人机家族中，四旋翼系统的机械结构最为简单、紧凑，对称的旋翼可同时完成逆时针或顺时针旋转，这种旋翼布局可以抵消螺旋桨引起的陀螺效应，产生更大的升力。注意到，在 MEMS（微机电）、新型传感器及新型材料等相关技术的推动下，搭载MIMUs（微惯性测量元件）、小型成像设备（照相机、摄像机）、磁罗盘、GPS接收机等导航设备的四旋翼系统还可实现近地面环境下的导航、定位与通信。

本文对四旋翼无人机的姿态控制系统开展专门研究。为确保飞行控制系统在风力扰动、陀螺效应、重力及旋翼惯量矩等诸多物理效应[2-3]影响下的控制效果，在传统自适应反步滑模控制（ABSMC）算法基础上，提出融合浸入与不变（I&I）原理的ABSMC算法，涉及滑模面的选择以提升系统鲁棒性，反步法的设计以抑制系统抖动，Lyapunov函数的选择以确保系统状态收敛等内容。同时，在对自适应滑模器控制率和自适应率的选择上，引入了基于I&I原理的误差流型设计理念，确保了系统的稳定性，提升了控制精度与扰动估计误差收敛效果。这部分研究内容将在第2～4节进行详尽阐述。作为必备基础内容，本文开篇给出四旋翼系统动力学模型及控制系统结构。

1 四旋翼系统动力学模型及控制系统结构

飞行控制方面，在外部传感器已提供了卓越的导航信息、机载电池已提供了稳定的动力能源的情况下，我们还需要对飞行状态进行数学建模。其中，由于6个自由度中的姿态与位置具有直接耦合关系，是否实现精确的姿态控制直接影响后续速度与位置控制的效果。

1.1 系统动力学模型

考虑到未知大幅度外部扰动的影响，结合文献[4]，建立非线性四旋翼姿态系统的动力学模型，表示为

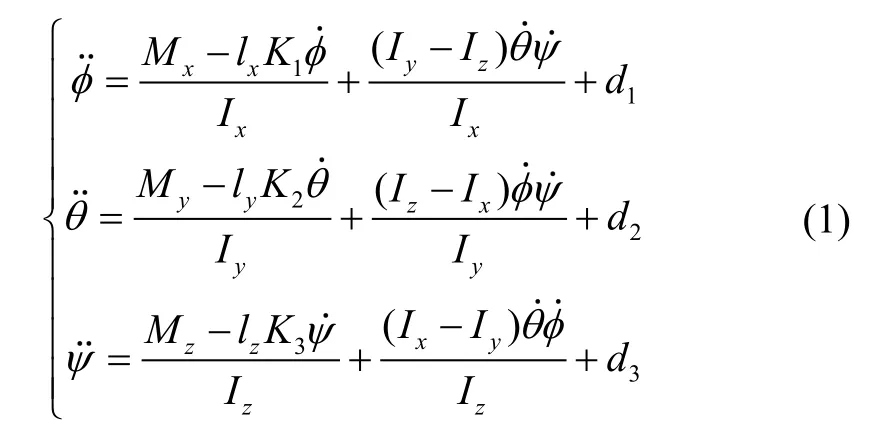
1.2 控制系统结构

如前所述，四旋翼系统中，姿态与位置存在直接的耦合关系，即横滚角/俯仰角的变化直接引起机体向前后/左右移动，因此，位置系统并不仅仅由位置控制量实施控制，还要由实时的姿态角进行调节。所设计的控制系统结构如图1所示。该系统为双闭环结构，通过信号发生器给出期望的位置轨迹和期望的偏航角，在位置控制器中根据位置系统动力学方程以及期望的位置计算出两个期望的虚拟姿态角后连同给定的期望偏航角送至姿态控制器，这样外环是实施PD控制率的位置系统，其输出是四旋翼的总体升力控制量，内环是本文研讨的姿态系统输出的三个姿态角的控制力矩。

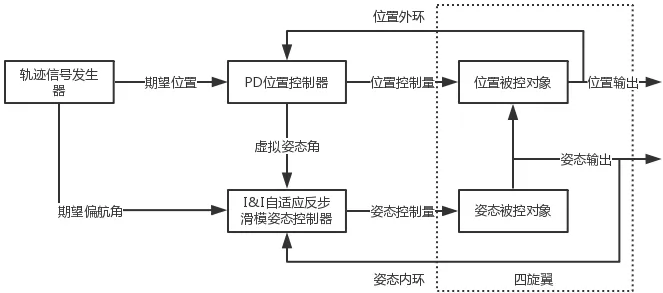
图1 四旋翼控制系统结构图Fig.1 Structure diagram of quadrotor control system

如文献[5-6]所述，在双闭环结构的控制系统中，内环的动态性能对外环的稳定性影响很大。针对这一问题，工程上一般使用内环收敛速度大于外环的控制策略。在上述四旋翼控制系统中，内环的姿态跟踪误差会影响外环位置系统的稳定性，进而对整个系统的稳定性造成影响。我们考虑通过合理地选取内环姿态控制率和自适应率，来确保整机系统的稳定性。具体方法是：控制率的设计结合了反步法，解决了系统抖动、控制不连续等问题；自适应率的设计中引入了额外的补偿项，保证了估计误差的收敛性，也提高了系统的抗干扰能力。第3节将给出详尽的设计方法。

2 自适应反步滑模控制器(ABSMC)设计

由于姿态系统是整个飞行控制的关键，国内外相关实验室、高校和科研机构已投入了大量研究工作，文献[7-9]着眼于 PID、滑模、自适应等诸多控制方法的研究，致力于获得更优的非线性控制效果，以提升系统的控制性能。

滑模控制方法的优点是当系统到达滑模面时，其运行状态只取决于滑模面，而与系统的原参数无关（抑制了参数不确定性[10]）。由于该性能是通过控制量的高频抖动换取的，此方法在实际工程中受到限制。注意到，反步法是一种基于Lyapunov函数的构造性方法，其首先将系统分解为低阶的子系统，然后分别设计各子系统的Lyapunov函数和虚拟控制量，再一步步反推，从而确保整个系统的稳定性。结合两者的优势，以下以横滚角子系统为例，给出传统ABSMC的实现原理。

改写式(1)中滚转角子系统的动力学模型，表示为

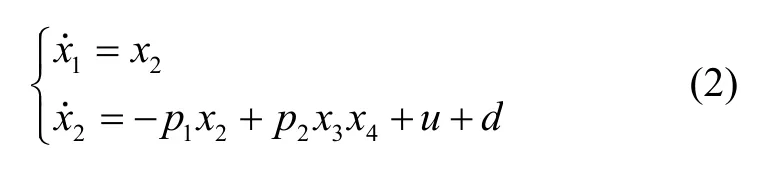
定义位置误差：

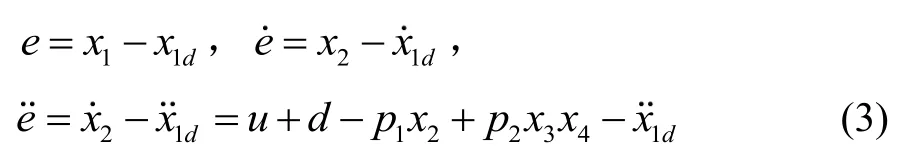
其中，x1d表示横滚角的期望值。

定义估计误差：

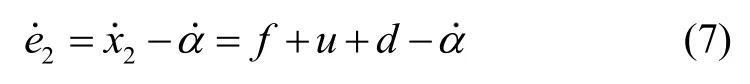
由滑模设计方法，设计滑模面为

其中，系数λ1＞0，则：

引入自适应算法，取Lyapunov函数，表示为

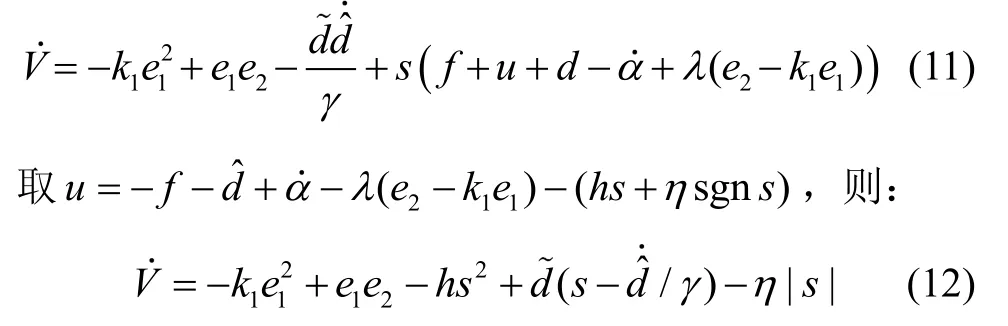
诚然，该设计方法可以保证系统全局是渐进稳定的。然而，系统对未知扰动估计误差的动态变化过程是无法调节的，这一现象虽然不会影响系统最终的稳定性，但有时会对系统的暂态响应造成严重的影响。

基于浸入与不变原理的自适应方法可以很好地解决这个问题。

3 基于浸入与不变原理（I&I）的自适应反步滑模控制器设计

I&I原理是通过设计流型并保持其吸引与不变，来维持系统稳定的。本文对误差估计建立流型，通过对控制率和自适应率的设计确保估计误差收敛到0。

仍以横滚角子系统为例，根据式(2)及式(7)中关于f的定义，有：

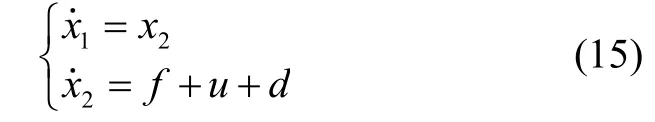
定义误差流型：

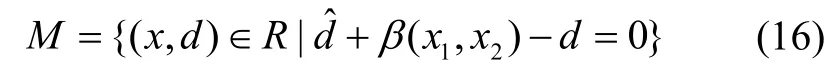
假定上述流型能够不变，则扩展横滚角子系统模型，对照公式(15)，有：

由公式(4)～(6)的反步法设计Lyapunov函数，为了保证负定，需要再设计函数，根据式(16)及式(17)中关于的定义，有：

以下完成控制率设计，令：

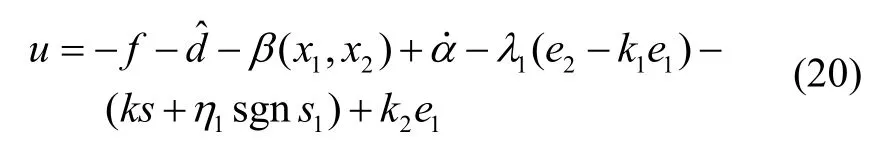
对扰动估计误差求导，有：

4 稳定性分析

由于滑模控制的切换增益η1需大于扰动估计误差绝对值的最大值才能保证负定，这里令有：

注意到，指数形式的趋近率可以改进系统的动态品质，但随着符号函数的引入而带来的不连续性问题却容易造成系统控制量的抖动。为了进一步抑制抖动发生，可采用相应的双曲正切函数为较小的正数）代替符号函数这部分内容将在后续数字仿真与分析中予以证明。

由于欧拉角各角度具有相同的特性，其余两个子系统的设计可参照完成，在此不再赘述。

5 数字仿真

5.1 仿真条件与初值

参照文献[12]中关于 PD外环位置系统中虚拟控制量的选取，得到：

该姿态系统动力学模型的参数取值如表1所列。

表1 姿态系统动力学模型中参数取值Tab.1 Parameter values in the dynamic model of attitude system

5.2 仿真结果与分析

图2给出了I&I方法下，姿态系统状态的相平面，从中可以看出，通过对控制率和自适应率的设计，确保了系统误差及其变化率收敛到0，整个系统渐进稳定。

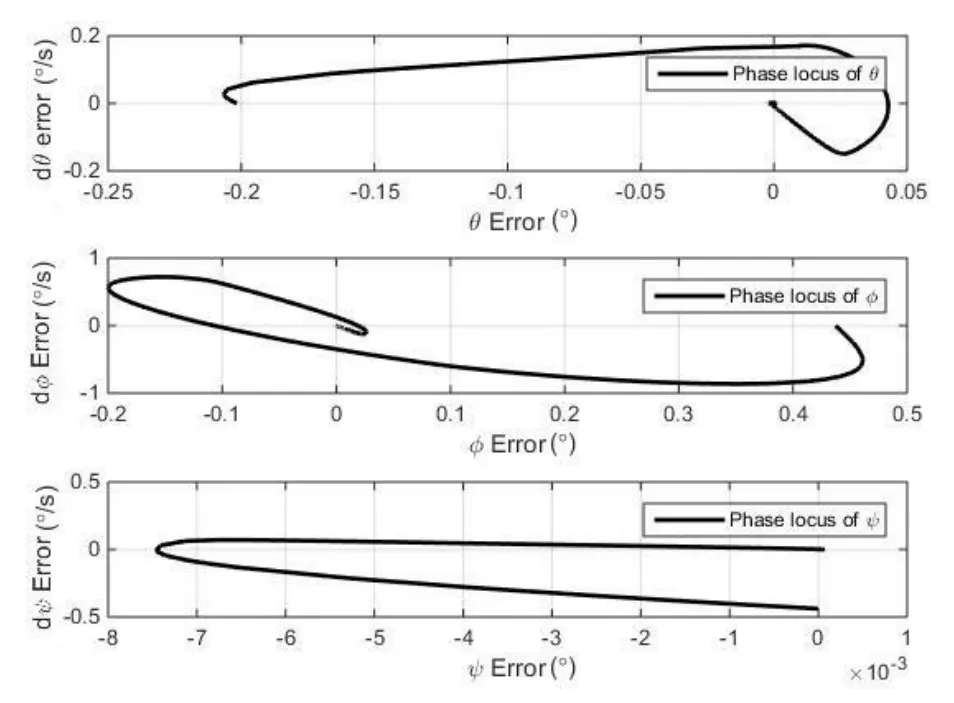
图2 姿态系统误差相平面Fig.2 Error phase plane for attitude system

为了比较滑模运动中趋近率的设计在采用及未采用连续切换函数时两种情况对系统控制量的影响，图3和图4分别给出了在符号函数、双曲正切函数作用下，系统控制量的变化曲线。

图3 符号函数作用下的控制量变化曲线Fig.3 Changing curves of controlled variables by sign function

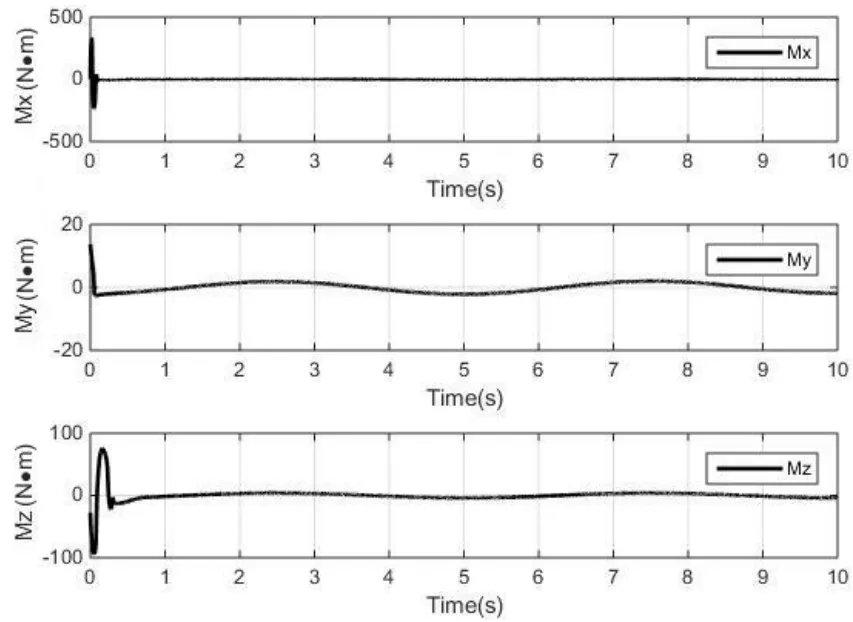
图4 双曲正切函数作用下的控制量变化曲线Fig.4 Changing curves of controlled variables by hyperbolic tangent function

图5 传统ABSMC方法的三轴扰动力矩估计Fig.5 Tri-axial torque disturbance estimates by classic ABSMC

图 5和图 6分别给出了相同仿真条件下，传统ABSMC和本文方法所获得的三轴扰动力矩估计效果，其中，红色虚线代表实际真值，黑色实线代表估计值。图7和图8为对应的扰动估计误差。

可以看出，传统ABSMC对扰动的跟踪误差较大，本文方法由于在自适应率中引入I&I原理，从而大幅提高了对外部未知扰动的适应能力，指数率及比例积分形式的补偿项促使收敛速度不断提升，更快地调整了扰动估计与给定扰动相一致。图8表征了三轴扰动估计误差已完全收敛，进一步直观地验证了这一效果。

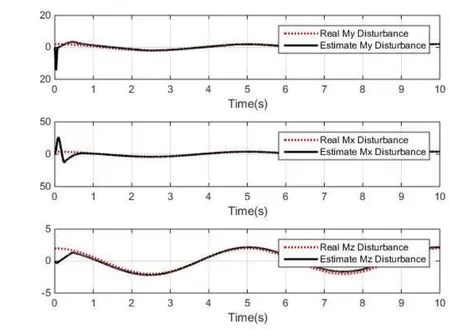
图6 本文方法的三轴扰动力矩估计Fig.6 Tri-axial torque disturbance estimates by method adopted

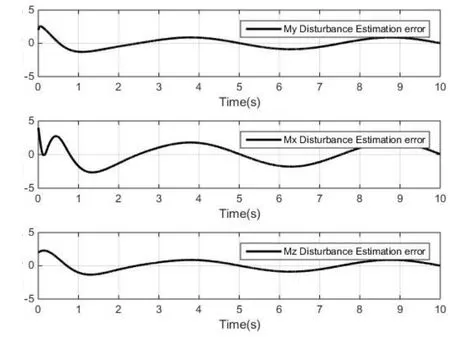
图7 传统ABSMC方法的三轴扰动力矩估计误差Fig.7 Tri-axial torque disturbance estimates error by classic ABSMC

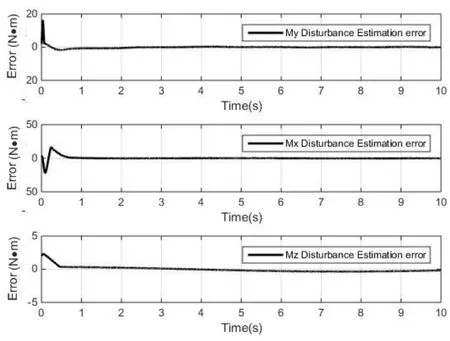
图8 本文方法的三轴扰动力矩估计误差Fig.8 Tri-axial torque disturbance estimates error by method adopted

图9和图10分别给出了相同仿真条件下，传统ABSMC和本文方法所获得的欧拉角角度跟踪效果，其中，红色虚线代表期望角度，黑色实线代表实际角度。选用有限时间偏差平方值积分（ISE）的比值B来衡量二者的跟踪效果，在仿真时间10 s时有：

式(27)表明本文方法在10 s内跟踪误差平方的累加和仅为传统方法的11.2%，控制精度大幅提高。

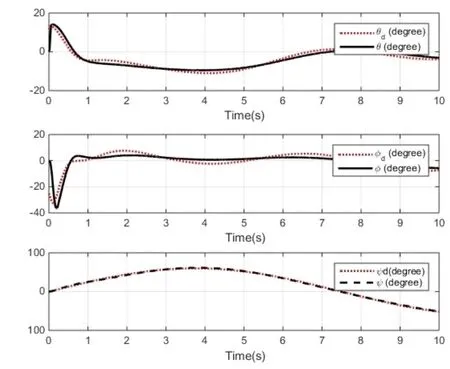
图9 传统ABSMC方法的角度跟踪效果Fig.9 Angle tracking by classic ABSMC

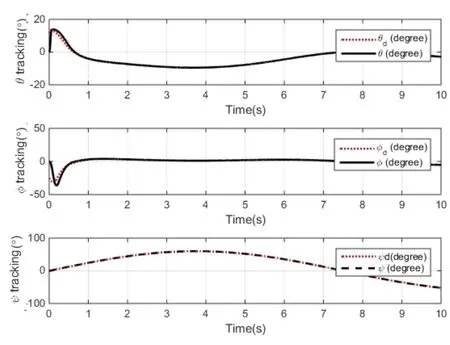
图10 本文方法的角度跟踪效果Fig.10 Angle tracking by method adopted

图 9～10这组对比图同样证明了基于 I&I原理的ABSMC方法在角度跟踪方面具有更优的性能。传统方法对于扰动估计的不足导致了跟踪的误差较大，而本文方法可以对外部扰动做出及时地估计，在提高鲁棒性的同时，进一步提升了控制精度。

6 结 论

本文对四旋翼无人机的姿态系统开展专门研究，以横滚角子系统为例，探讨基于浸入与不变（I&I）原理的自适应反步滑模控制（ABSMC）策略，在确保物理系统稳定工作的前提下，解决了飞行控制系统对于较大幅度外部不确定扰动下的精确误差估计与稳定跟踪问题。相同条件下的仿真对比表明，基于I&I原理的ABSMC在获得优化的扰动估计效果方面具备更卓越的性能，可实现三轴扰动估计误差的完全收敛以及姿态角的无差跟踪。同时，该方法为滑模控制中控制率与自适应率的设计提供了模型参考。

（References）：

[1]范云生, 曹亚博, 赵永生.四旋翼飞行器轨迹跟踪控制器的设计与验证[J].仪器仪表学报, 2017, 38(03): 741-749.Fun Y S, Cao Y B, Zhao Y S.Design and validation of trajectory tracking controller for quadrotor[J].Chinese Journal of Scientific Instrument, 2017, 38(3): 741-749.

[2]张居乾, 任朝晖, 周来宏, 等.基于指数收敛的四旋翼无人机鲁棒自适应飞行控制[J].中国惯性技术学报,2016, 24(4): 548-553.Zhang J Q, Ren C H, Zhou L H.Robust and adaptive flight control of quadrotor based on exponential convergence[J].Journal of Chinese Inertial Technology, 2016, 24(4): 548-553.

[3]窦景欣, 孔祥希, 闻邦椿, 等.四旋翼无人机模糊自抗扰姿态控制及稳定性分析[J].中国惯性技术学报,2015, 23(6): 824-830.Dou J X, Kong X X, Wen B C.Attitude fuzzy active disturbance rejection controller design of quadrotor UAV and its stability analysis[J].Journal of Chinese Inertial Technology, 2015, 23(6): 824-830.

[4]Bertrand S, Guénard N, Hamel T, et al.A hierarchical controller for miniature VTOL UAVs: Design and stability analysis using singular perturbation theory[J].Control Engineering Practice, 2011, 19(10): 1099-1108.

[5]Jankovic M, Sepulchre R, Kokotovic P V.Constructive Lyapunov stabilization of nonlinear cascade systems[J].IEEE Transactions on Automatic Control, 1996, 41(12): 1723-1735.

[6]Zhao B, Xian B, Zhang Y, et al.Immersion and invariance based adaptive attitude tracking control of a quadrotor UAV in the presence of parametric uncertainty[C]//2014 33rd Chinese Control Conference.Nanjing,China, 2014: 1932-1937.

[7]Yang K S, Cheng C C.Robust adaptive controller design for a quadrotor helicopter[J].Applied Mechanics &Materials, 2013, 284-287: 2296-2300.

[8]Gong X, Hou Z C, Zhao C J, et al.Adaptive backstepping sliding mode trajectory tracking control for a quad-rotor[J].International Journal of Automation and Computing, 2012, 9(5): 555-560.

[9]Pounds P E, Bersak D R, Dollar A M.Stability of small-scale UAV helicopters and quadrotors with added payload mass under PID control[J].Autonomous Robots,2012, 33(1): 129-142.

[10]曾令全, 王美琪, 张佳琦, 等.基于滑模控制的大型变速风机的最大风能捕获研究[J].东北电力大学学报,2017, 37(2): 31-38.Zeng L Q, Wang M Q, Zhang J Q, et al.Maximum power point tracking of large scale variable speed wind turbine based on sliding mode control[J].Journal of Northeast Electric Power University, 2017, 37(2): 31-38.

[11]侯小燕, 薛文涛, 张晨.基于浸入与不变的气动弹性系统反演滑模控制[J].航天控制, 2016, 34(4): 3-9.Hou X Y, Xue W T, Zhang C.Backstepping sliding mode control of aeroelastic system based on immersion and invariance[J].Aerospace Control, 2016, 34(4): 3-9.

[12]刘金琨.先进PID控制MATLAB仿真(第4版)[M].北京: 电子工业出版社, 2016.

Backstepping sliding mode control of quadrotor attitude system based on immersion and invariance

XIA Lin-lin1, CONG Jing-yu1, MA Wen-jie2, ZHAO Yao1, LIU Hui-min3
(1.School of Automation Engineering, Electric Power University, Jilin 132012, China;2.Science College, Northeast Electric Power University, Jilin 132012, China; 3.College of Mechnical and Electrical Engineering, Qingdao Agricultural University, Qingdao 266109, China)

When it comes to the issue of quadrotor’s attitude system stabilization under large uncertain external disturbances, an adaptive backstepping sliding mode controller (ABSMC) on basis of immersion and invariance(I&I) principle is designed.Firstly, the dynamic model of quadrotor’s attitude system with unknown large disturbances is established.In sequence, the roll subsystem is designated to be set as an illustration, and the corresponding sliding mode control strategies related to the backstepping form & reaching law are designed and introduced accordingly.Specifically, the I&I principle is invoked in the design process for disturbance estimates error manifold, that is, choosing suitable adaptive rate helps to gain error manifold’s invariant and attractive properties, guaranteeing the estimates error mentioned above converges to zero as expected.Finally, the stabilization analysis and numerical simulation are carried out.The results illustrate that, under adverse operation circumstances, the summation of tracking error square within 10 s by I&I principle descend to 11.2%of that derived by typical ABSMC, and the control precision is tested to be drastically enhanced.

quadrotor; attitude system, immersion and invariance; backstepping method; sliding mode control

U666.1

A

1005-6734(2017)05-0695-06

10.13695/j.cnki.12-1222/o3.2017.05.024

2017-07-07；

2017-09-15

国家自然科学基金项目（61503073）；吉林省科技厅自然科学基金项目（20170101125JC）；吉林省教育厅科学技术研究项目（20171005）；吉林市科技局杰出青年项目（20166005）

夏琳琳（1980—），女，博士，教授，从事导航系统研究。E-mail: prettylin521@aliyun.com

联 系 人：刘惠敏（1983—），女，博士生，讲师。E-mail: lhmgct@126.com