人类通信行为中的标度律

王春娟，林振权

（温州大学物理与电子信息工程学院，浙江 温州 325035）

人类通信行为中的标度律

王春娟，林振权

（温州大学物理与电子信息工程学院，浙江 温州 325035）

对钱学森书信的响应时间和信件长度进行统计分析，发现信件长度服从系数为0.005的负指数分布，同时信件响应时间和信件长度在一定范围内存在标度关系。该结果揭示了人类通信行为的一个内在规律，为通信机制的进一步挖掘提供了实证依据。

人类动力学；通信模式；幂律分布；标度特性

0 引言

最近几年里，通过对人类活动历史（包括通讯、工作和娱乐）的海量数据库的分析，越来越多的证据显示人类许多行为的时间统计特性无法用泊松分布刻画。2005年，Barabási和他的同事对3 188位用户收发的共129 135封电子邮件进行了统计分析，发现用户相继发送两封邮件的间隔时间服从的不是指数分布，而是幂函数分布。表现为邮件发送会密集出现在一段很短的时间内，然后会有很长一段时间没有任何邮件发出［1］。Oliveira和Barabási，以及Vázquez等［2-3］对达尔文、爱因斯坦和弗洛伊德的书信通信记录的研究发现，一封信在τ天被回复的概率可用指数为α=1.5的幂律尾衰减分布很好地近似。

而针对电子邮件的研究显示，人们发送电子邮件的间隔时间和响应时间服从α=1的幂律尾衰减分布。Vázquez等［3］经过研究指出人类动力学存在两大普适类，分别对应幂指数为α=1和α=1.5。紧接着许多学者就人类系统的普适性发生了激烈的争辩，认为在人类系统中提出的重尾分布的渐近幂律行为是否有足够的统计证据？简单地根据幂指数划分普适类的假设合理吗？对于有争议的普适类讨论话题和幂律问题，人类通信是很好的范例，在文献中被广泛关注。2008年，李楠楠等［4］对钱学森、鲁迅书信进行统计，发现钱学森信件的响应时间分布也服从幂律分布，但幂指数为2.1，据此对普适类的说法提出了质疑。2009年，曹盼盼等［5］选取了中国近代的茅盾、傅雷、陶行知和胡适等文化名人的书信，分析他们的通信行为同样得到了时间特性的幂律分布，且提出了社会环境对幂指数的影响。与此同时，Malmgren等［6］对16位作家、演员、政治家、科学家的电邮和通信数据进行分析，认为幂律的时间间隔是人类行为周期性、重复性和需求量变化的结果，随着年龄增长和社会角色的确定，人们趋向于每天周期性的重复某些活动，不会有太大程度的改变，并由此建立了一种级联式的非齐次泊松过程来描述这种行为的产生。该模拟结果对16位用户的电子邮件和书面通信行为有个很好的解释，揭示了不同通信活动可能存在着相似的驱动机制，为人类通信行为的研究提供了方向。

对于人类各种行为表现出来的幂律特性的起源，众多学者从不同的角度进行了尝试。Barabási等率先给出了基于个人决策的排队论解释，通过改变模型参数的取值使其适应不同的情况，尽管该模拟结果对于电子邮件和书面通信的重尾分布有个很好的解释，但还是存在着部分缺陷，该模型的核心与实质是把人类的行为看做执行一系列的任务，然而任务选择型机制并不能解释真实生活中全部的人类活动，比如浏览网页［7］，在线电影点播［8］，手机短信［9］等等。但是这些活动也展现出一些相类似的统计规律（胖尾时间间隔分布）。同时所研究的数据中也并没有包括一个人所参与的所有任务，于是有学者又在排队论的基础上提出了其他交互模型［10］。Kentsis等［11］注意到一封电子邮件或者书面信件的响应时间还依赖于通信发生时的社会内容，个体信件语义内容，任务的难度和社会关系等一系列复杂的影响机制。由此对Barabási的排队模型进行了深入探讨，随后根据许多实际情况国内学者提出了自身的生理活动［12］、兴趣［13］、截止时间［14］、记忆［15］等诸多影响机制，但始终没有得到统一共识。这些研究工作表明人类行为潜在的规律性和复杂性。

书面通信有别于人们在网络上的通信行为，它更能反映出人在社会中与人交流的真实情况，为进一步挖掘其内在统计规律，除研究信件的发信时间间隔和响应时间统计分布规律外，本文还提出信件长度这一属性，以反映人们在写信时难以察觉的心境和外部事件的影响。因此本文中将结合信件长度和响应时间两方面分析人类通信行为，并且将全部信件按其字数分为不同长度段，分析各不同长度段信件的响应时间分布之间的关系，为建立人类通信行为模型提供实证依据。

1 数据分析

本文采用了钱学森从1955年至2000年的通信数据，其中有1 782封信标注了信件的收信时间和回复时间，把它定义为响应时间τ，以天为单位。当同一个人在一段时间内发送了几封信件时，以最近一封信为收录时间计算响应时间，假设最后一封信激起回复，前面的信件并没有得到真正的回复，把它看做是信件的遗弃，以避免响应尺度的大量重叠。举个例子，在发短信时你收到了很多条来自同一个人的信息，人们不会逐条进行回复，而是就上一封内容做出回应，连带着告知前面信息有收到。然而在研究短信、邮件的时间特性时，由于个人隐私受法律保护，无法了解个体信件的语义内容，以至于无法明确是否是对此封信件的响应，导致不清楚是上段话题未完还是已经开始下一个话题，故等待时间不明确，把话题的完结当做长时间的响应做了处理［16］。而本文研究的钱学森书信中内容已经公开，且都标有收录时间，如10月4日的信收读，通过语义分析也能明确是否是对上封信件的响应，使响应时间的计算更精确。

以往学者在确定幂指数时，用了极大似然估计方法，结果一般依赖最小值的选取，在数据量有限的情况下幂指数会偏离真实值。本文对响应时间分布使用了补函数［17-20］。

对于幂律分布（1），在α＞1时有

补分布不仅可以消除尾部波动，还可以避免对数装箱方法中难以准确确定装箱宽度的问题，不丢失任何信息，在数据点较少的情况下，补分布统计更准确，对幂律特性有较好的表达［19］，在大量的实证研究中被广泛使用［5-6，12，17，20-21］。

2 实证结果

由于间隔时间分布受个人决策的优先级影响［1-3］，不能作为人类动力学的适当量度，因此要实现最终成功预测响应的统计性质，本文将注意力放在响应时间的统计上。首先是对钱学森信件的响应时间分布采用补分布函数，如图1所示，响应时间分布在双对数坐标下为幂律衰减尾分布，τ表示响应时间的横坐标，以天为单位。纵坐标用p（t≥τ）表示响应时间所对应的补分布概率。直线是对数据点的线性拟合，其中5≤τ≤100，负相关系数R=-0.996，响应时间的幂律衰减尾分布形式（1），其幂指数为α=2.6±0.02。与［4］相比偏大，这与本文收集数据和处理的方法有关，回信机制在整体上较快，随着统计方法的发展，其精确度会略有波动。而响应时间大于100天的只有17封信，只占大约总量的1%。

在分析人们在互联网上的行为时，认为传输文件大小分布属于帕累托分布，从而导致互联网上通信量的胖尾特性［21］。对此，本文对钱学森具有确切响应时间的信件按信件长度进行统计分析。信件长度数据来源于人工计数，为避免人为误差影响，数据以20字为统计字数段，每个统计字数段内各信件字数的加权平均值作为该字数段内信件的长度k。图2画出长度在63≤k≤1 490范围的通信量分布N（k），在数据中除去下垂头部的影响作线性拟合，结果在单对数坐标下为指数衰减分布。

其中λ=0.005。在图2的插图中给出了相应的补分布图，补分布线性拟合指数值与直接拟合结果一致。可以这样解释，在早期人们基于写信习惯和交流条件的限制，会按照相对稳定的模式进行书信往来，交流中轻易不会长篇大论。该结果与当前人们在即时交流通讯中表现出的规律并不相同，例如QQ群用户在线交流行为中每次发送QQ消息的字符数呈现出幂律尾分布［22］，类似地人们在互联网上传输文件的大小分布也是幂律形式［21］。可见现代通信的便利性使得人们的交流方式在不断改变。

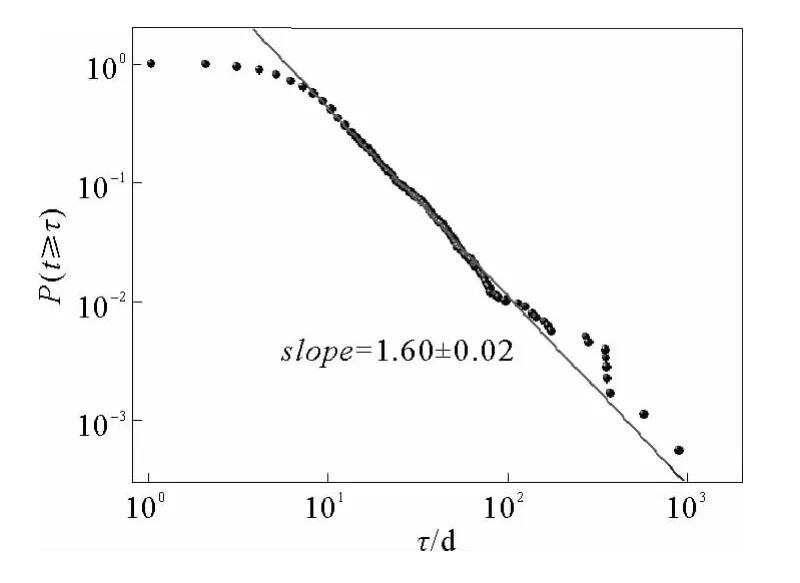
图1 钱学森书信响应时间的补分布Fig.1 Response time complementary cumulative distribution function of Qian Xuesen’s correspondence

图2 信件字数长度分布Fig.2 Empirical response size distribution of Qian Xuesen’s correspondence

进一步考察不同长度段信件的响应时间分布，并分析各不同长度段信件的响应时间分布之间的关系。以钱学森书信的响应时间分布为例，本文将钱学森有确切回复时间记录的全部信件按其字数分为不同长度段，其中72%的信件字数在165～572字之间，将此范围的信件分成4个字数长度段，每个统计字数段内各信件字数的加权平均值kc代表该字数段内信件的长度，如表1所示。

通过对k1～k4区间内钱学森写信响应时间的统计，分别得到其书信响应时间服从幂律尾分布，且幂指数与总体分布都接近α=2.6，随k的增大依次向下，如图3所示。说明在k1～k4区间的信件对响应时间的幂律尾分布做出了主要的贡献，而大于k4的范围由于数据不足没有明显的分布关系，除去这部分信件对整体的响应时间分布几乎没有影响。

在图4中，通过重新定标揭示了不同长度段信件的响应时间分布之间存在标度律，它们在相同的有特定标度指数的曲线上塌缩。横坐标为响应时间，纵坐标为累计通信量与信件长度补函数的比值。该结果可以表示为

表1 各字数段范围及kc取值Tab.1 The every word scope and kcvalue

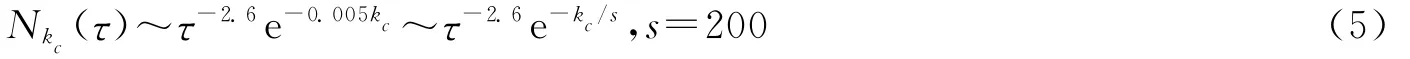
这里排除了偶尔写短信和长信的概率，假设个体写信内容长度是稳定地控制在k1～k4范围内。不同长度段信件的响应时间分布之间存在的标度律（5）反映了在统计范围中的信件存在一个特征字数长度，s=200，对应图2中的峰值。

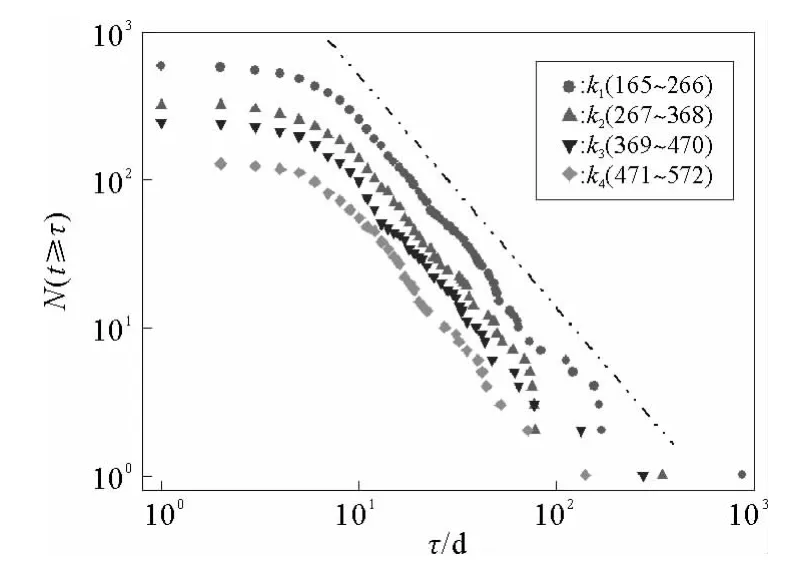
图3 不同信件长度下的响应时间补分布Fig.3 Response time distribution for communication scales

图4 信件长度与响应时间的标度关系Fig.4 Collape of I distributions for correspondence pattern

3 总结和讨论

本文统计了钱学森一生中与人交流的通信数据，发现信件长度服从系数λ=0.005的负指数分布，其特征字数长度约200字。该结果不同于快捷的群用户聊天中字符数的分布［22］或者互联网传输文件的大小分布［21］，书信较注重思想上的交流，字数跨度大多集中在165～572字的范围内，而QQ即时通讯在交流时可以简单的回复“Yes”或者“No”，使得字符少的占总体比重较大，对于钱学森书信字数一般不少于63个字，这更类似于人们写日记的长度。通过对钱学森书信响应时间的分析，发现响应时间的幂律尾分布受多方面因素影响，如地理位置、节假日、出差、由他处转来、任务难度等。举个例子，钱学森在1985年2月11日给夏振坤的一封信中写到：“您在去年5月14日写给我的信和两篇尊著收到后就细读过，但您提出的问题我也一时说不出来什么，所以就放下了。一放就是九个月！请您原谅！”。这也符合Oliveira等对通信模式复杂性的探讨［2-3，11］。

本文还分析了在不同信件长度下信件的响应情况，发现在信件长度相对稳定的区间分别表现出依次向下的幂律尾分布，且幂指数与总的响应时间分布近乎一致，也就是说在这段稳定的交流中人们趋向于相似的通信机制，信件响应时间的幂律特性主要由字数在165～572的信件贡献，大的信件长度对响应时间的分布几乎没有影响。通过重订标得到了数据的塌缩，暗示了响应时间和信件长度之间潜在的标度关系，对文献［1］中电子邮件大小和等待时间关系的探讨给予进一步的实证依据。相信随着信息挖掘的发展，在足够的信息量情况下，可能会有更丰富的标度关系。那么设想在纷繁多样的个体行为模式下可能隐藏着某种共同的人类通信机制，并且这种潜在的模式可能不区分古今时代，对不同的个体和通信方式普遍适用，是一种潜在的人类通信普适模式。对它的深入研究将有利于优化资源配置，便于商家制定商业决策，如邮政通信行业可以采取相应的策略提高其性能指标。其应用价值和商业潜质在不断兴起的新型服务行业中也会不断地体现。对于其他通信领域这只是一个初探，有待于有兴趣的学者们进一步挖掘。

［1］Barabási A L.The origin of bursts and heavy tails in human dynamics［J］.Nature，2005，435（7039）：207-211.

［2］Oliveira J G，Barabási A L.Human dynamics：Darwin and Einstein correspondence patterns［J］.Nature，2005，437（7063）：1251-1253.

［3］Vázquez A，Oliveira J G，DezsöZ，et al.Modeling bursts and heavy tails in human dynamics［J］.Physical Review E，2006，73（3）：036127.

［4］李楠楠，张宁，周涛.人类通信模式中基于时间统计的实证研究［J］.复杂系统与复杂性科学，2008，5（3）：43-47.

Li Nannan，Zhang Ning，Zhou Tao.Empirical analysis on temporal statistics of human correspondence patterns［J］.Complex Systems and Complexity Science，2008，5（3）：43-47.

［5］曹盼盼，阎春宇.人类通信模式的幂律分布和Zipf定律［J］.复杂系统与复杂性科学，2009，6（4）：51-56.

Cao Panpan，Yan Chunyu.The power law and Zipf's law in human communication patterns［J］.Complex Systems and Complexity Science，2009，6（4）：51-56.

［6］Malmgren R D，Stouffer D B，Campanharo A S L O，et al.On universality in human correspondence activity［J］.Science，2009，325：1696-1705.

［7］赵庚升，张宁，周涛.网页浏览中的标度行为研究［J］.统计与决策，2009（1）：18-19.

Zhao Gengsheng，Zhang Ning，Zhou Tao.Study on scaling behavior in webpage visiting［J］.Statistics and Decision，2009（1）：18-19.

［8］Zhou T，Kiet H A T，Kim B J，et al.Role of activity in human dynamics［J］.Europhys Letters，2008，82（2）：28002.

［9］Hong W，Han X P，Zhou T，et al.Heavy-tailed statistics in short-message communication［J］.Chinese Physics Letters，2009，26（2）：028902.

［10］Rybsli R，Buldyrev S V，Havlin S，et al.Scaling laws of human interaction activity［J］.PNAS，2009，106（31）：12640-12645.

［11］Oliveira J G，Barabási A L.Correspondence patterns：mechanisms and models of human dynamics（replay）［J］.Nature，2006，441：E5-E6.

［12］Nakamura T，Kiyono K，Yoshiuchi K，et al.Universal scaling law in human behavioral organization［J］.Physical Review Letters，2007，999（13）：138103.

［13］韩筱璞，周涛，汪秉宏.基于自适应调节的人类动力学模型［J］.复杂系统与复杂性科学，2007，4（4）：1-5.

Han Xiaopu，Zhou Tao，Wang Binghong.The model of human dynamics based on adaptive interest［J］.Complex Systems and Complexity Science，2007，4（4）：1-5.

［14］邓竹君，张宁，李季明.截止时间对人类动力学模型的影响［C］//郭近利，周涛，张宁，等.人类行为动力学模型.香港：上海系统科学出版社.2008：29-34.

Deng Zhujun，Zhang Ning，Li Jiming.The impact of deadline on human dynamics model［C］//Guo Jinli，Zhou Tao，Zhang Ning，et al.The Dynamics of Human Behavior.Hongkong：Shanghai system science press，2008：29-34.

［15］Vázquez A.Impact of memory on human dynamics［J］.Physica A，2007，373（1）：747-752.

［16］Wu Y，Zhou C S，Xiao J H，et al.Evidence for a bimodal distribution in human communication［J］.PNAS，2010，107（44）：18803-18808.

［17］Ethan P W，Brian J E，Jessica L G.On estimating the exponent of power-law frequency distribution［J］.Ecology，2008，89（4）：905-912.

［18］Clauset A，Shalizi C R，Newman M E J.Power-law distribution in empirical data［J］.SIAM Review，2009，51（4）：661-703.

［19］史定华.网络度分布理论［M］.北京：高等教育出版社，2011：34-40.

［20］Newman M E J.Power laws，Pareto distribution and Zipf's law［J］.Contemporary Physics，2005，46（5）：323-351.

［21］Crovella M E，Bestavros A.Self-similarity in world wide web traffic：evidence and possible causes［J］.IEEE/ACM Trans Networking，1997，5（6）：834-846.

［22］王洪川，郭进利，樊超.基于群聊天记录的人类行为动力学分析［J］.计算机应用与软件，2012，29（7）：9-10.

Wang Hongchuan，Guo Jinli，Fan Chao.Group chat records based human behavior dynamics analysis［J］.Computer Applications and Software，2012，29（7）：9-10.

Scaling Law in Human Communication Pattern

WANG Chun-juan，LIN Zhen-quan
（School of Physics and Electronic Information Engineering，Wenzhou University，Wenzhou 325035，China）

Through the statistics from Qian Xuesen's communication，we present that the size distribution of the letters obeys an exponent distribution with the best fitting exponentλ=0.005.In addition，we reveal a scaling law relating response time and the size of replied letter within a certain range.It is possible to characterize inherently statistical regularities in communication behavior.Our findings provide theoretical evidence for the future excavation of the communication mechanism.

human dynamics；communication pattern；power-law distribution；scaling-law

N94

A

1672-3813（2013）03-0025-06

2012-12-12

国家自然科学基金（10875086，11175131）

王春娟（1987-），女，吉林榆树人，硕士研究生，主要研究方向为人类动力学。

（责任编辑 耿金花）