由动态信号揭示社团结构

杨春林，张四平

（1.兰州商学院信息工程学院计算机系，兰州 730020；2.兰州大学物理科学与技术学院，兰州 730000）

由动态信号揭示社团结构

杨春林1，张四平2

（1.兰州商学院信息工程学院计算机系，兰州 730020；2.兰州大学物理科学与技术学院，兰州 730000）

就一个社团网络系统，基于不同的链接，给出了观察动态信号及分析动力学变量快照的方法。结果表明如果节点能够正确排序，当网络体系处于退同步状态时，通过几张动力学变量快照就足以确定社团网络结构。此外，当社团结构演变为规则晶格时，动力学变量将表现为某种正弦波形式，这将有助于进一步揭示无序社团网络结构。

社团结构；Rossler振子；快照；退同步

社团结构，也就是由诸多社团组成的网络结构。在许多社会的［1-4］、生物的［5-6］、技术的［7-9］网络中已经发现，单个社团内节点链接浓密，而社团之间链接稀疏。就一个社团网络体系，关键不在节点，而是链接。在全局范围内，连接不同社团之间的链接对网络的效率起着决定性的作用。因此仅从对动态信号的观察来识别网络结构很重要，也可以通过保护或者攻击这些重要链接来防护或更有效地销毁网络。当网络连接是已知的，有许多途径可以找出社团结构［10-12］。然而，在很多情形下，网络链接并不已知，仅能通过一些动态信号来观察体系。这样，从可能的观察中找出社团结构对于某些任务是很关键的。此外，在可以使用相关性矩阵，因为单个社团里面的节点之间比属于不同社团里的节点之间更有关联性。而且，这种关联性可以给出一种节点的划分，这种划分与该社团网络结构相匹配。这种方法可以在一般情况下使用，此时体系并非完全同步。然而，在一定条件下，存在一种更快的方法：仅仅通过观察动态信号的几张快照就可以找出社团结构。进一步，通过这种快速方法还可以发现在每一个社团里面是否有局部规则结构。

为说明这种快速方法，首先引进一些预备数学知识从同步状态的稳定分析开始［13-14］。假设每一个节点遵循非线性动力学并且不同的节点通过网络连接耦合。具体来说，每个振子孤立时的行为可以描述为

其中，x是d维向量，F（x）是速度场。不失一般性，选择标准振子模型Rossler振子：

其中，x=［x，y，z］T且

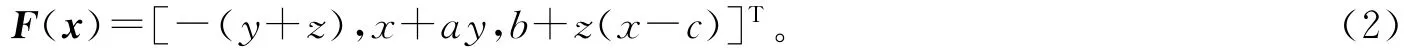
如此选定Rossler振子的参数，它表现为混沌振动。网络动力学方程可写为

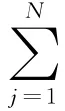
由于体系可以用方程（3）表述，因此，控制无穷小向量δxi（t）≡xi（t）-s（t）随时间的演化变化方程为

其中，DF（s）与DH（s）是相应于向量函数值s（t）的雅克比矩阵。对角化耦合矩阵G所产生的一组特征值为｛λi｝（i=1，…，N），相应的归一化特征向量用e1，e2，…，eN表示。在一般真实情况下特征值是非负的［15］，因此可以排序为0=λ1＜λ2≤…≤λN。比值λN/λ2越小，网络的同步性就越强［16-17］。做变换δy=O-1·δx，其中，O为一矩阵，它的每一列为一组特征向量，因此可得方程（4）的分块对角非耦合形式为

令K=ελi（i=2，…，N）是归一化的耦合参数，进而方程写为

对于方程（5）的最大李雅普诺夫指数是主要稳定函数Ψ（K）［18］，如果Ψ（K）是负数，一个小的扰动将以指数形式从同步状态衰减，因此系统是稳定同步的；如果Ψ（K）是正的，一个小的扰动将被放大且系统不再同步。

在区域［K1，K2］中，函数Ψ（K）是负数，其中K1，K2完全依赖于节点动力学控制函数F（x）和输出函数H（x）。因此，对于K1＜K＜K2，所有的特征向量（本征模）是横向稳定的，并且网络是同步的。可给出同步区域边界条件：

当违反此条件时，网络将变成退同步。如果条件（7）违背，体系将发散，因此仅关注条件（6）。从以前的研究中［19-22］可知，如果仅仅几个模式跳出同步区域［K1，K2］，也就是说ελi＜K1且K1＜ελi+1＜K2，i是个小整数，那么网络将变为退同步且动力学变量的变化将有相应于从e2到ei的特定形式。对于社团结构，如果它有M个社团，那么λ1=0，λ2到λM互相靠得很近，却与λM+1很好地分离（见图1）。相应于特征向量e2到eM都有一种社团形式：在一个社团里面的元素有一种相干形式（要么是连续不断，要么表现为正弦波，这种形式依赖于社团的网络结构）而且他们十分不同于属于不同社团里面的元素。因此如果i≤M，所有的不稳定模式都有一种社团结构，动力学变量的非相干性将表现出一种结构的相似性，也就是说如果节点被正确地分类，绘出可视信号将表现出明显的社团结构，如图2所示。进一步，因为特征值λ2到λM很好地偏离于λM+1到λN，所以有一个比较大的参数范围可以观察这种现象，即K1/λM+1＜ε＜K1/λ2。例如，对于Rossler体系，选择a=b=0.2，c=9。

图1 具有M个子网的社团网络特征谱图Fig.1 A schematic show of eigenvalue spectra for clustered networks with Mrandom subnetworks

图2 一个随机社团网络的不同节点动态变量xi的典型轮廓Fig.2 A typical of the dynamical variable xiof different nodes for a random clustered network

所对应的雅克比矩阵为

其主稳函数如图3所示。此时K1≈0.2且K2≈4.62。如果社团网络有图1所示的相同参数，那么可用于观察这种现象的参数范围是0.25＜ε＜1，与被λ2∶0＜ε＜1所引起的全局不同步区域相比这种现象是非常稳定的。

作为例子，考虑如下社团网络模型；将N个节点分成M个社团，每个社团有n=N/M个节点，在单个社团内一对节点被连接的概率为ps，而属于不同社团的节点连接的概率为pl，这样形成一个社团随机网络。特别是社团之间的链接数远远小于社团内部的链接数，结果发现与一个小的pl参数区更相关。

图2表明一个典型的结果就是可以观察到由于违背条件（6）所引起的退同步Rossler体系的动态变量。作为人为网络，社团结构已知且节点能够被正确排序。在图2中可以清楚地看到社团结构。对于真实的例子，一个简单的方法是通过动力学变量的值去排序，因为在一个社团里面的节点有相近的值。在排序以后，动态变量将有一个阶梯形式，每一阶梯相应于一个社团。

图3 对于Rossler振子网络，方程5的主要稳定函数Ψ（K）随K的变化图Fig.3 For the rossler oscillator network，an example of the mastor stabilty functionΨ（K）calculated form Eq.5

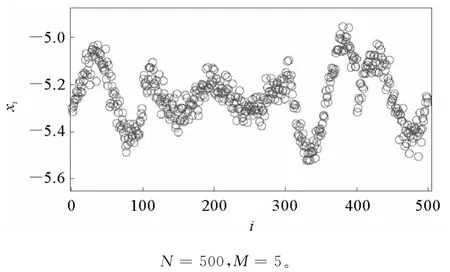
图4 对于每个规则晶格社团的一个社团网络不同节点动态变量xi的典型轮廓Fig.4 A typical profile of the dynamical variable xiof different nodes for a clustered network

通常，观察这种现象的参数范围较大，而且很快，因为仅通过几个快照足以确定社团结构，所以这个方法很实用。但是，当前的问题是需要假定每个社团是一个无序网络，例如随机、无标度、小世界网络，当每一个社团变成一个规则晶格时，每个社团内相应于λ2到λM将有一个正弦波形式。因此，当体系违背条件（6）变成退同步时，动力学变量也可以有一个正弦波形式，如图4所示。在这种情况下，如果节点的正确排序是未知的，那么对于找出阶梯的排序方法将是无效的。因此，基于上述工作和其他学者所提出的各种算法［23-26］，我们希望通过适当改变或增加一些算法准则来推广这种算法，找出正弦波形式，进而揭示网络结构。以后的工作将主要集中对这个方法的推广并且提供更多具体的解析基础，或采取某种改进使它适用于更多真实的动力学系统。

综上所述，对于社团随机网络，如果节点能够正确排序，当网络体系违背条件（6）而处于退同步状态时，仅仅通过几张动力学变量快照就足以确定社团网络结构。此外，还发现，当社团结构演变为规则晶格时，动力学变量将表现为某种正弦波形式，这将有助于进一步揭示无序社团网络结构。

［1］Zachary W W.An information flow model for conflict and fission in small groups［J］.J Anthropol Res，1977，33（4）：452-473.

［2］Watts D J，Dodds P S，Newman M E J.Identity and search in social networks［J］.Science，2002，296：1302-1304.

［3］Girvan M，Newman M E J.Physical sciences-applied mathematics［J］.Proc Natl Acad Sci U S A，2002，99（12）：7821-7826.

［4］Motter A E，Nishikawa T，Lai Y-C.Large-scale structural organization of social networks［J］.Phys Rev E，2003，68（3）：036105.

［5］Ravasz E，Somera A L，Mongru D A ，et al.Hierarchical organization of modularity in metabolic networks［J］.Science，2002，297：1551-1554.

［6］Spirin V，Mirny L A，Protein complexes and functional modules inmolecular networks［J］.Proc Natl Acad Sci USA ，2003，100（21）：12123-12128.

［7］Milo R ，Shen-Orr S，Itzkovitz S，et al.Network motifs：simple building blocks of complex networks［J］.Science，2002，298：824-826.

［8］Vazquez A，Pastor-Satorras R，Vespignani A.Large-scale topological and dynamical properties of the internet［J］.Phys Rev E，2002，65（6）：066130.

［9］Eriksen K A，Simonsen I，Maslov S，et al.Modularity and extreme edges of the internet［J］.Phys Rev Lett，2003，90（14）：148701.

［10］Girvan M ，Newman M E J.Community structure in social and biological networks［J］.Proc Natl Acad Sci USA，2002，99（12）：7821-7826.

［11］Wildinson D M，Huberman B A.A method for finding communities of related genes［J］.Proc Natl Acad Sci USA，2004，101（suppl 1）：5241-5248.

［12］Palla G，Derenyi I，Farkas I，et al.Uncovering the overlapping community structure of complex networks in nature and society［J］.Nature，2005，435：814-818.

［13］陈娟，陆君安.复杂网络中尺度研究揭开网络同步化过程［J］.电子科技大学学报，2012，41（1）：9-11.

Chen Juan，Lu Jun′an.Mesoscales reveal synchronization processes in complex networks［J］.Journal of University of E-lectronic Science and Technology of China，2012，41（1）：9-11.

［14］Huang L，Chen Q F，Lai Y Ch，et al.Generic behavior of master-stability functions in coupled nonlinear dynamical systems［J］.Phys Rev E，2009，80（3）：1-6.

［15］Jost Jand Joy M P.Spectral properties and synchronization in coupled map lattices［J］.Phys Rev E，2002，65（1）：016201.

［16］Nishikawa T，Motter A E，Lai Y Ch，et al.Heterogeneity in oscillator networks：are smaller worlds easier to synchronize［J］.Phys Rev Lett，2003，91（1）：014101.

［17］Motter A E，Zhou C S，Kurths J.Enhancing complex-network synchronization［J］.Europhys Lett，2005，69（3）：334-340.

［18］Pecora L M，Carroll T L.Master stability functions for synchronized coupled systems［J］.Phys Rev Lett.1998，80（10）：2109-2112.

［19］Huang L，Park K，Lai Y Ch，et al.Abnormal synchronization in complex clustered networks［J］.Phys Rev Lett，2006，97（16）：164101.

［20］Hunag L，Lai Y Ch，Robert A G.Alternatingsynchronizability of complex clusterednetworks with regular local structure［J］.Phys Rev E，2008，77（1）：016103.

［21］吕翎，邹家蕊，杨明，等.大规模富社团网络的时空混沌同步［J］.物理学报，2010，59（10）：6864-6866.

LüLing，Zou Jiarui，Yang Ming，et al.Synchronization of spatiotemporal chaos in large scale rich club network［J］.Chin Phys Soc，2010，59（10）：6864-6866.

［22］杨浦，郑志刚.基于动力学的复杂网络结构识别速度研究［J］.物理学报，2012，61（12）：1-2.

Yang Pu，Zheng Zhigang.Analysis the convergency speed of estimating the network topology based on the dynamical synchronization［J］.Chin Phys Soc，2012，61（12）：1-2.

［23］张聪，沈惠璋.网络自然密度社团结构模块度函数［J］.电子科技大学学报，2012，41（2）：186-187.

Zhang Cong，Shen Huizhang.Modularity function for community structure based on natural density of networks［J］.Journal of University of Electronic Science and Technology of China，2012，41（2）：186-187.

［24］邓小龙，王柏，吴斌，等.基于信息熵的复杂网络社团划分建模和验证［J］.计算机研究与发展，2012，49（4）：726-727.

Deng Xiaolong，Wang Bai，Wu Bin，et al.Modularity modeling and evaluation in community detecting of complex network based on information entropy［J］.Journal of Computer Research and Development，2012，49（4）：726-727.

Referring Clustered Structure from Dynamical Signals

YANG Chun-lin1，ZHANG Si-ping2
（1.School of Information Engineering，Lanzhou University of Finance and Economics，Lanzhou 730020，China；2.School of Physical science and Technology，Lanzhou University，Lanzhou 730000，China）

For a clustered network system，based on the different links，this paper presents the method that observed dynamical signals and analyzed the snapshot of the variation of the dynamical.It is show that a few snapshots are enough to determine thecluster structure when the system becomes desynchronizedafter nodes ordered.Moreover when each cluster becomesa regular lattice，the variation of the dynamicalcan have sine wave form in each cluster.This will help to refer clustered structure of the disordered network.

clustered structure；Rossler oscillator；snapshot；desynchronization

O415.6

A

1672-3813（2013）03-0020-05

2013-03-03

杨春林（1966-），男，甘肃酒泉人，学士，副教授，主要研究方向为复杂网络研究。

（责任编辑 耿金花）