考虑碳排放权交易的双寡头有限理性博弈分析

赵令锐，张骥骧

（南京航空航天大学经济与管理学院，南京 211106）

考虑碳排放权交易的双寡头有限理性博弈分析

赵令锐，张骥骧

（南京航空航天大学经济与管理学院，南京 211106）

对有限理性Cournot模型进行改进，将其引入到碳排放权交易市场，建立一个考虑碳排放权交易的有限理性双寡头博弈模型。然后利用非线性动力学方法讨论该模型均衡点的存在性与稳定性，并进行数值仿真。研究发现碳排放权交易对系统有重要影响：碳排放权交易价格和二氧化碳产生系数不仅影响企业在均衡点的产量，还影响系统的稳定性。运用延迟反馈控制法对陷入混沌状态的系统进行控制，可以使系统重新回到Nash均衡状态。

碳排放权交易；有限理性；Cournot模型；混沌

0 引言

碳排放权交易是指政府根据区域内的环境容量和资源情况确定总的二氧化碳排放量，然后按照一定的标准，通过免费分配、拍卖、定价出售等方式，把总碳排量以碳排放权配额的形式分给该区域内的各个企业，企业可以在市场上对该配额进行交易，但企业在生产经营过程中的碳排放总量不能超过其最终拥有的碳排放权配额，否则将面临巨额罚款和制裁，从而达到对区域内二氧化碳排放的总量控制。通过碳排放权交易，碳排放边际成本高的企业将购买碳排放权而付出成本，碳排放边际成本低的企业将出售碳排放权而获得收益。这样，碳排放权成为一种调节资源配置的商品，能够刺激企业提高资源利用效率、采用环保技术和设备等方式减少二氧化碳的排放，最终实现二氧化碳排放的总成本最小化以及保护环境和节约资源。

虽然目前中国作为发展中国家而没有强制减排的义务，但为应对全球气候变化和国际碳排放权交易对中国带来的冲击和影响，以及推动中国产业结构调整和经济的可持续发展，中国积极参与减缓气候变暖行动，在北京、上海等七省市启动碳排放权交易试点。国家进行碳排放权交易需要企业的积极参与，而企业进行碳排放权交易活动后，其生产、技术、利润等等各方面都会受到一定的影响。因此，分析碳排放权交易对企业生产决策、效益等的影响，有助于为碳排放权交易政策的实施提供充分的理论依据，对碳排放权交易制度的制定和实施也有较强的指导和借鉴意义。

对碳排放权的研究，主要集中在碳排放权的初始分配［1-2］、碳排放权的交易价格［3］、碳排放权交易的经济效应［4］等问题上。在完全竞争市场中，市场均衡时边际减排成本与碳排放权的市场均衡价格相等［1］。但是，碳排放权交易可能严重依赖于行业的市场结构，完全竞争市场的情况并不适用于寡头垄断市场。在寡头垄断市场中，企业很可能通过自己的买卖行为对碳排放权的交易价格产生较大影响，使之偏离市场均衡价格，这样市场有效配置资源的功能得不到很好的发挥。因此，对寡头垄断市场中进行碳排放权交易的企业的博弈行为进行分析，具有十分重要的价值。

自1883年Cournot提出了经典的产量决策Cournot模型后，许多国内外学者把有限理性、非线性成本等因素引入Cournot模型，运用改进后的模型对寡头垄断市场进行研究。Puu［5］和Agiza等［6］分别将有限理性引入双寡头和三寡头博弈模型，研究发现了分岔、混沌和奇异吸引子等复杂的动力学现象。Elabbasy等［7］研究了非线性成本的有限理性三寡头博弈模型，并进行了混沌控制。达庆利等［8］针对耐用品寡头垄断市场，比较分析了具有相异成本的两企业同时博弈的动态Cournot模型和多目标动态Cournot模型。潘玉荣等［9］定性分析不同理性双寡头博弈模型，发现寡头为获取前期竞争优势而不断加快产量调整速度将导致系统的不稳定性。胡荣［10］通过引入“学习效应”思想研究具有学习效应的有限理性Cournot竞争模型，结果表明学习效应对动态Cournot竞争复杂性有显著影响。姚洪兴等［11］分析了差异化策略的两组动态Cournot模型并进行仿真，结果表明同一团队适当的利润分配及调整参数的变化有利于系统稳定性，引入时滞使系统达到稳定状态。

本文把有限理性和碳排放权交易引入到经典的Cournot模型中，建立考虑碳排放权交易的双寡头有限理性产量博弈模型，分析该模型均衡点的存在性与稳定性，讨论产量调整速度对系统所处状态的影响。通过数值模拟，研究模型的动态演化过程。最后运用一种有效的混沌控制法对陷入混沌状态的系统进行控制，使系统重新回到Nash均衡状态。

1 模型建立

假设寡头垄断不完全竞争市场上有生产相同产品的两企业，且满足要求：

1）每个企业的产量决策发生在离散的时间周期n=0，1，2，…，qi（n）表示企业i（i=1，2）在n期的产量，第n期内市场的总供给量为Q=q1（n）+q2（n）；第n期的价格P 由Q（n）通过逆需求函数P=a-bQ决定，其中a，b为正的常数，a为市场上该产品的最高价格。企业的生产成本为线性函数，即Ci（qi）=ciqi，其中单位产品的生产成本ci＞0。

2）企业生产过程中产生的二氧化碳数量与其产量qi线性相关，记为kiqi，其中ki为企业i的二氧化碳产生系数，k1，k2为非负常数。企业可以自行减排，企业i的碳减排量为di，减排成本系数为βi（βi＞0），则减排成本为βidi。因此，企业i的总的碳排放量为kiqi-di。

3）企业免费获得的初始碳排放权为y0，则企业i的碳排放权交易量为y0-（kiqi-di），交易价格为p。若y0-（kiqi-di）＞0，表示企业i出售剩余的碳排放权；若y0-（kiqi-di）＜0，表示企业i购买不足的碳排放权，且y0-（kiqi-di）=-（y0-（kjqj-dj））。

因此，企业i在第n期的利润函数分别为

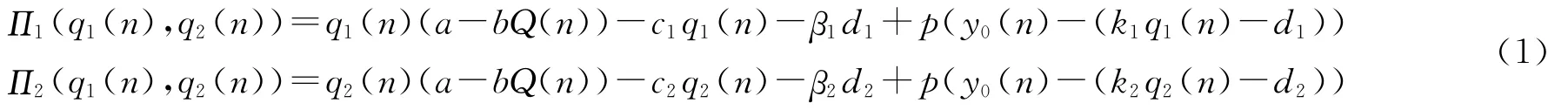
对Πi（q1（n），q2（n））关于qi（n）求偏导，可得企业i边际利润：

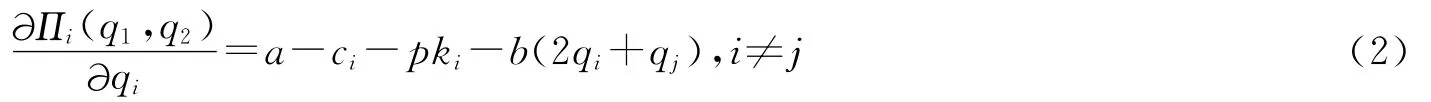
令c′i=ci+pki，即c′i为企业i单位产品的总变动成本，由单位产品的生产成本ci与单位产品的碳排放成本pki两部分构成，则式（2）可简化为

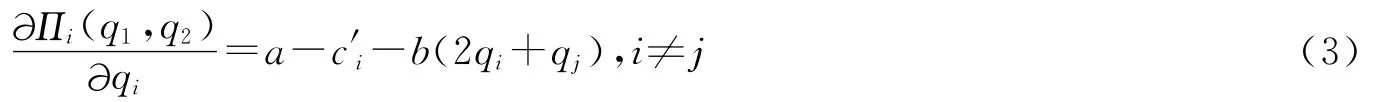
由于现实中市场信息的不完全性和企业自身条件的限制，企业决策时只能达到有限理性，不能对未来市场的需求情况进行完全预测，因此假定企业依据对边际利润的局部估计确定其产量［12］。如果企业在第n期的边际利润为正，则其将会在第n+1期增加产量；反之如果边际利润为负，就会减少产量。因而可得到企业i在第n+1期的产量为

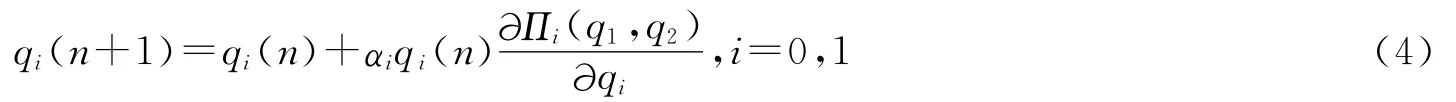
其中，αi是一个正的参数，表示企业i的产量调整速度。于是把式（3）代入式（4）中，可得双寡头有限理性产量博弈模型：

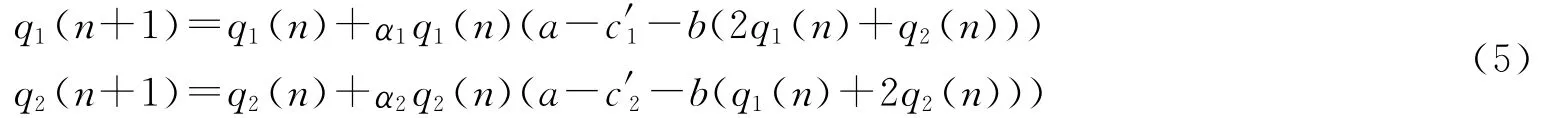
2 模型分析

为研究双寡头产量博弈模型（5）的动态行为，本节对系统的非负均衡解进行研究。在系统（5）中，令qi（n+1）=qi（n），i=1，2，可得到代数系统：

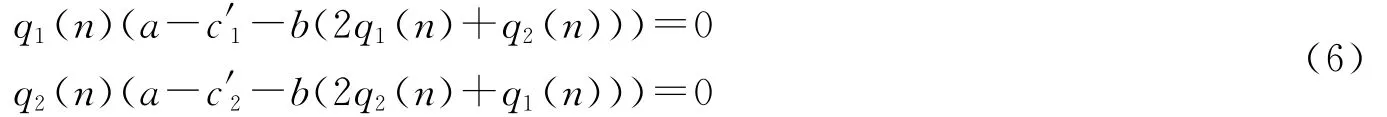
解式（6）可以求得4个非负均衡点为

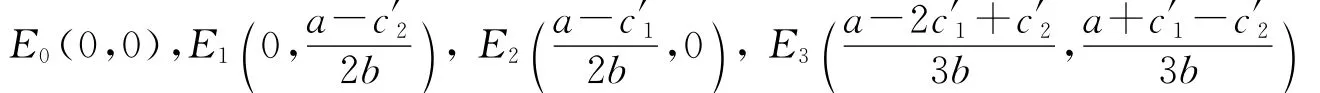
显然，E0，E1，E2为有界均衡点（垄断均衡）；当a+c′2＞2c′1，a+c′1＞2c′2时，E3为 Nash均衡点。下面研究这4个均衡点的稳定性，首先计算系统（5）的Jacobian矩阵，即

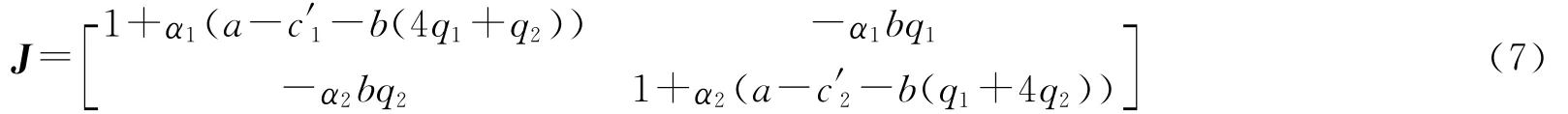
定理1 有界均衡点E0，E1，E2是不稳定均衡点（鞍点）。

证明：把E0的值代入式（7）可得到E0的Jacobin矩阵J（E0），然后解矩阵J（E0）可求得有界均衡E0处的两个特征值分别为

其中，a为市场上该产品的最高价格，c′i为企业i的单位产品的总变动成本，由单位产品的生产成本与单位产品的碳排放成本两部分构成。在现实经济中，产品的市场最高价格肯定会高于总变动成本，否则企业为获得利润是不会选择生产该产品，即a＞c′i，故有λi＞1，即E0是一个不稳定点。E0对应的是两企业都未进入市场，市场还很广阔，企业应该努力降低单位产品的生产成本和二氧化碳的产生系数，以便迅速地垄断该市场。

同样可求得在有界均衡E1处的两个特征值分别为

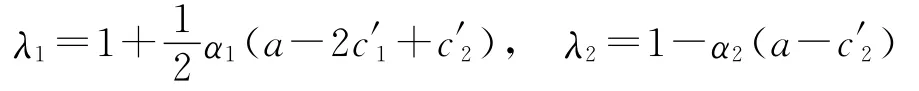
根据经济学理论，产品的市场最高价格比企业单位产品的总变动成本要大得多，寡头企业间的产品的单位生产成本相差不大，二氧化碳生产系数相差较小，因而总变动成本相差不大，从而有a-2c′1+c′2＞0，所以λ1＞1，即E1是一个不稳定点。E1点所对应的是单寡头垄断市场，企业2完全垄断市场，而企业1的产量为零。造成这种单寡头垄断市场的出现很可能是由于企业2的单位产品的生产成本远低于企业1，或者企业1的二氧化碳产生系数远高于企业2。在利润的驱使下企业1肯定不会满足于现状，它会尽量减少生产成本，降低二氧化碳产生系数，调整α1从而增加产量进入市场。而企业2将会相应地采取应对措施阻碍企业1对市场的占领，保持自己的市场占有率。

由于E1和E2具有对称结构，故在有界均衡E2处，有着与E1相似的情况。原命题得证。

定理2 当α1，α2满足0＜2α1A+2α2B-α1α2AB＜6，4α1A+4α2B-α1α2AB＜12（其中A=a-2（c1+pk1）+c2+pk2，B=a+c1+pk1-2（c2+pk2）时，Nash均衡点E3是稳定的。

证明：在Nash均衡点E3处Jacobin矩阵为

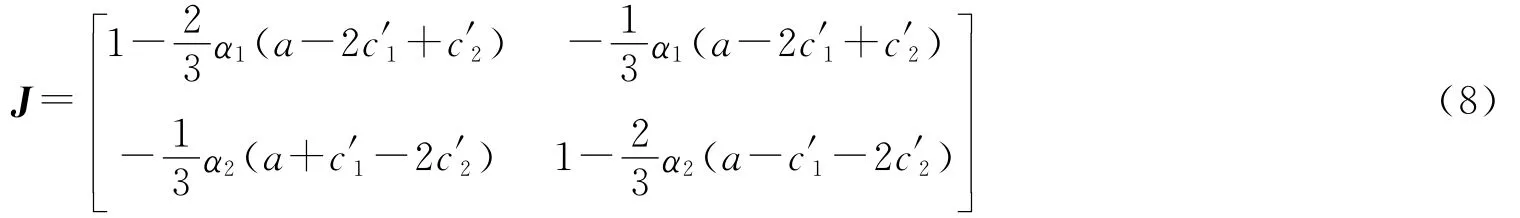
它的特征方程为f（λ）=λ2-trJλ+det J=0，其中trJ和det J分别是矩阵J的迹和行列式：

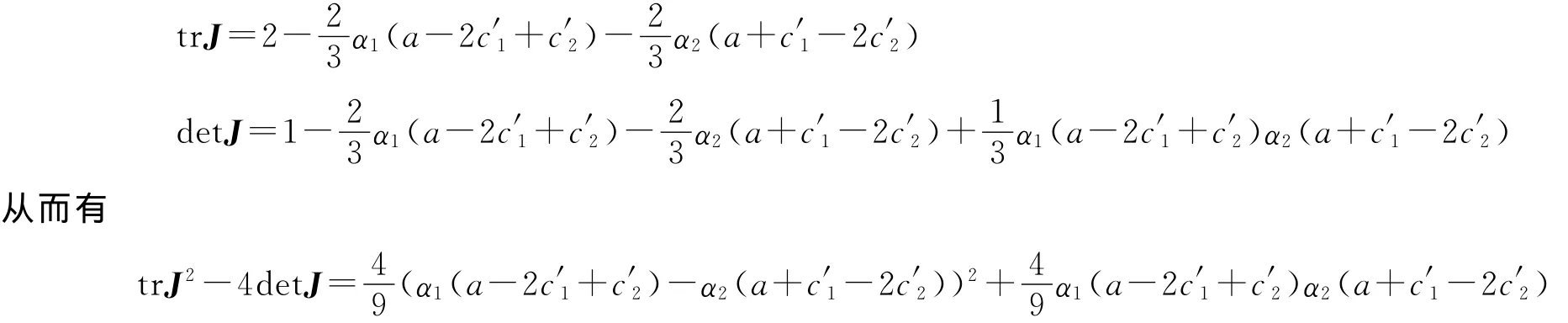
由于是基于a+c′2＞2c′1，a+c′1＞2c′2的假设前提，故trJ2-4det J＞0，这表明 Nash均衡E3的特征值为实的。根据Jury条件［13］，Nash均衡点E3稳定的充分必要条件为

把trJ，det J代入式（9），整理得Nash均衡E3稳定的充分必要条件为α1，α2应满足条件：

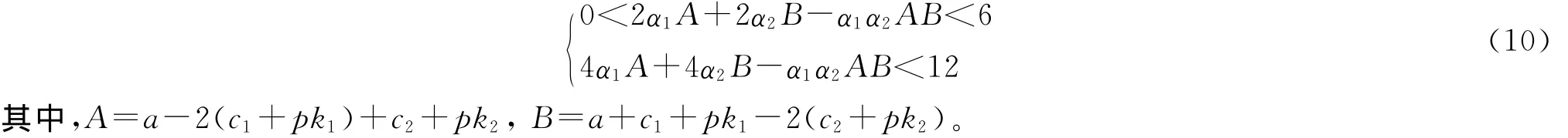
显然，式（10）定义了一个Nash均衡点E3的稳定区域，在该区域内E3是稳定的，但是若α1，α2不满足式（10）而超出了这个区域，E3将变得不稳定。原命题得征。

由于两企业都是有限理性的，两者的产量博弈不可能立即达到Nash均衡状态，需要进行多次重复博弈才能最终趋于平衡。而一旦某一企业或者两企业的产量调整速度过快，使得α1，α2超出了式（10）所定义的区域，都将会使系统的稳定性发生改变。但是α1，α2的不同取值不会改变Nash均衡点的大小，即对E3没有影响。碳排放权的交易价格p和二氧化碳的产生系数ki对系统有重要影响，不仅会影响企业在均衡点的产量，即对E3有影响，也会影响均衡点的稳定性，即若p，ki的取值超出了式（10）所定义的区域系统将不稳定。ki由企业的生产设备和技术等决定，在一定周期内不变。p由市场决定，是企业的不可控因素，一般可通过政府政策、市场调节等手段加以调控。限于篇幅，关于碳排放权的交易价格对双寡头博弈模型的具体影响，将另文讨论。

3 数值模拟

为了更直观地分析双寡头有限理性产量博弈模型（5）的动态行为，选取一定的参数值对该系统进行数值模拟，描绘系统（5）的动态演化过程、奇异吸引子等图。

假定参数初始取值为a=10，b=3，c1=1，c2=1，p=1，k1=0.1，k2=0.3。

图1描绘了其他参数取初始值，α2=0.1时，系统（5）随企业1的产量调整速度α1变化的动态演化过程，并描绘出系统出现的奇异吸引子。从图中可以看出，当α1＜0.3时，Nash均衡点E3（1.01，0.94）是稳定的，但随着α1的增大，E3将变得不稳定；当α1＞0.3并逐渐增大时，系统由Nash均衡状态逐步进入分岔、混沌状态。

图1 双寡头有限理性博弈模型（5）的动态演化及奇异吸引子Fig.1 Dynamic process of duopoly game with bounded rationality and strange attractor of system（5）

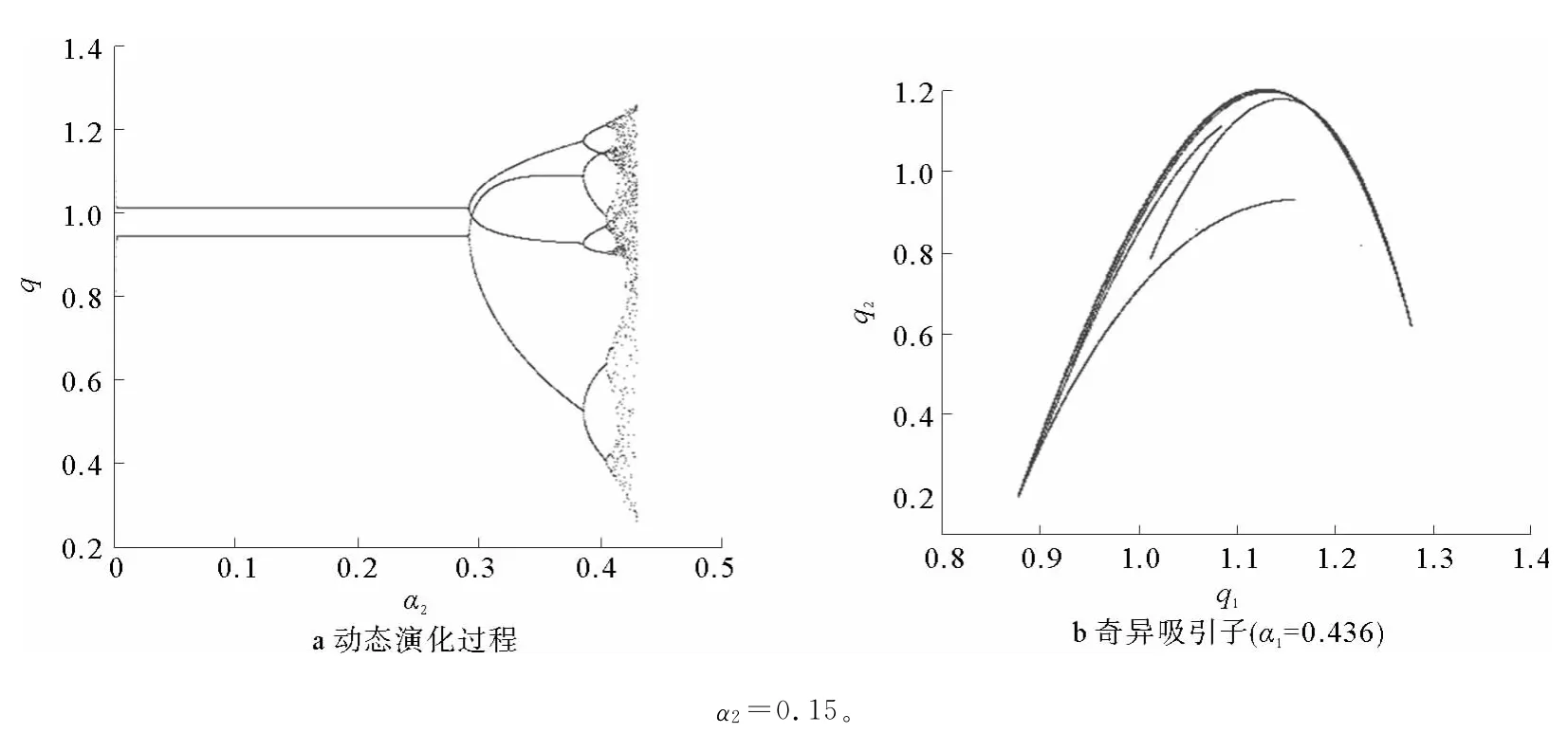
图2 双寡头有限理性博弈模型（5）的动态演化及奇异吸引子Fig.2 Dynamic process of duopoly game with bounded rationality and strange attractor of system（5）

图2描绘了其他参数取初始值，α1=0.15时，系统（5）随企业2的产量调整速度α2变化的动态演化过程，并描绘出系统出现的奇异吸引子。从图中可以看出，当α2＜0.29时，Nash均衡点E3（1.01，0.94）是稳定的；但随着α2的增大，E3将变得不稳定；当α2＞0.29并逐渐增大时，系统由Nash均衡状态逐步进入分岔、混沌状态。

为进一步验证产量调整速度变化所引起的混沌现象，分析系统是否对初始值有敏感性依赖。图3分别描绘了当其他参数取初始值，α1=0.15，α2=0.436（此时系统处于混沌状态），两企业产量的初始值为（q10，q20）和（q10+0.000 001，q20）时，产量q1关于时期t的变化图。从图中可以看出，刚开始企业1的两条产量演化曲线几乎一样，但在经过多次迭代后就开始产生明显的分离，即初始条件的细微变动都会极大地影响博弈结果。

图3 企业1产量q1对初始产量的敏感依赖性Fig.3 Sensitive dependence on initial conditions of player l

通过上述模拟分析发现，双寡头有限理性产量竞争，经过多次博弈后会出现稳定、分岔和混沌3种复杂的情况。当企业的产量调整速度αi较小时，双寡头在多次博弈后最终将会趋向唯一的Nash均衡；但若αi太大，超过某一临界值，其博弈结果便具有很大的不确定性，多次博弈后双寡头产量竞争将会进入分岔或混沌状态。一旦陷入混沌的市场中，博弈双方初始条件的细微变化都会极大地影响最终结果，并使企业对市场的变化情况不能进行有效的预测，这对企业来说是不利的，其生产决策等受到很大的影响。

4 混沌控制

通过模型分析和数值模拟发现，当企业的产量调整速度超过临界值后，系统（5）将失去稳定而进入复杂的分岔、混沌状态，此时企业初始条件的细微调整都会产生极大的不可预测性，这是企业所不愿面对的。因此，对系统（5）进行混沌控制以保证其处于稳定均衡状态是企业所必须做的。

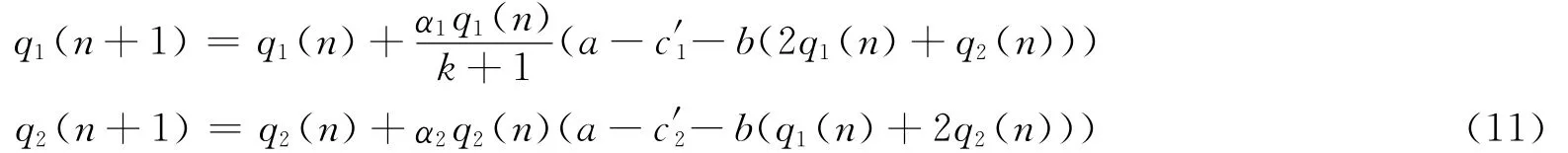
其中，k为控制因子，则系统（10）在Nash均衡E3处Jacobin矩阵为

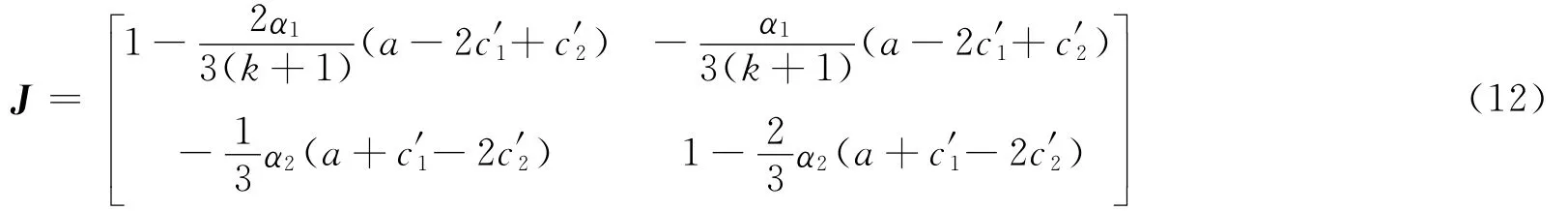
根据特征方程（12）和Jury条件即可求出k的有效取值范围。

图4描绘了其他参数取初始值，α1=0.429，α2=0.1时，双寡头有限理性产量博弈模型的混沌控制图。从图中可以看出，控制因子k很小时，系统处于混沌状态；随着k的逐步增大，当k＞0.44时，系统（5）便由混沌状态经过分岔后重新回到了Nash均衡状态。图5描绘了当α1=0.429，α2=0.1，k=0.5，企业初始产量为（0.8，0.5）时，企业产量由混沌状态逐步稳定到Nash均衡的时间变化历程。

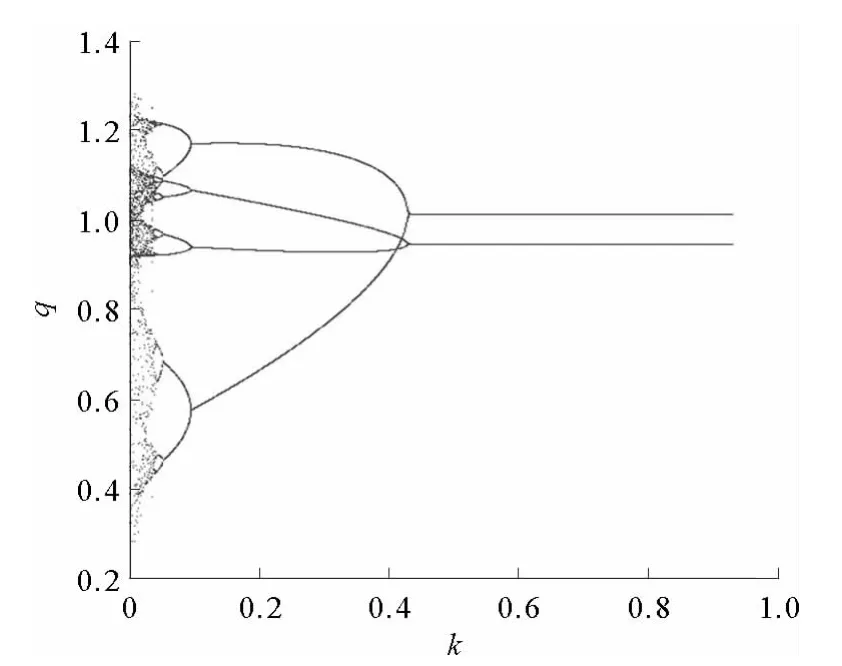
图4 双寡头博弈混沌控制Fig.4 Bifurcation diagram of chaos control

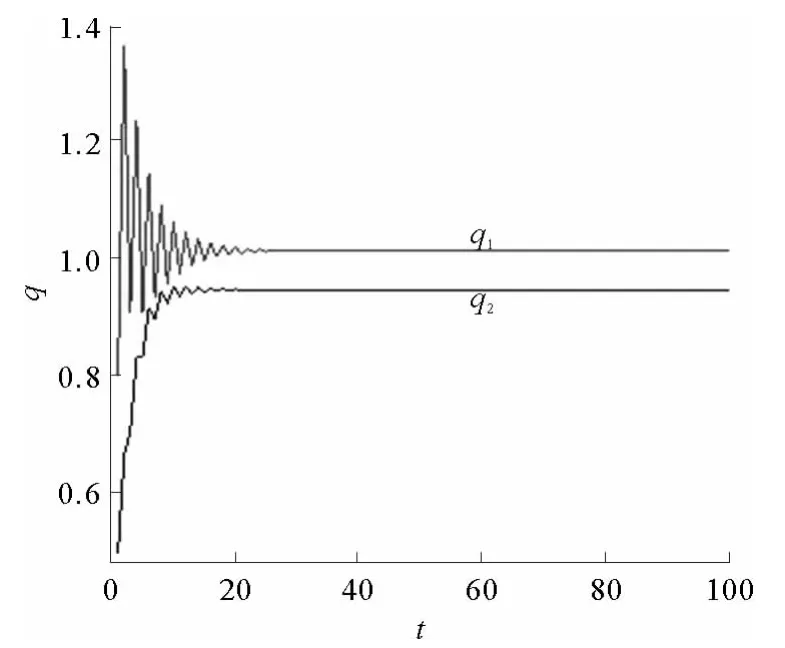
图5 企业产量变化的时间历程Fig.5 Stabilization of nash equlibrium

5 结论

本文把有限理性及碳排放权交易引入到经典的Cournot模型中，建立了考虑碳排放权交易的双寡头有限理性产量博弈模型，对该模型进行了稳定性分析，并且计算出了该模型的稳定区域。分析发现，若系统参数超出了稳定区域，该系统则会进入分岔、混沌状态。当企业进行碳排放权交易后，系统的稳定性受到影响，其中碳排放权交易价格和企业的二氧化碳产生系数不仅会影响企业在均衡点的产量，还会影响均衡点的稳定性；而碳减排量和减排成本系数对系统的稳定性无影响，只影响到企业最后的利润。

此外，还对博弈过程进行了数值模拟。模拟结果表明，企业的产量调整速度的大小可以导致双方博弈Nash均衡的稳定性发生变化。当企业的产量调整速度较小时，系统最终都会动态地趋向Nash均衡；但若调整速度太大，超过某一临界值，博弈结果便具有很大的不确定性，多次博弈后双寡头产量竞争将会进入分岔或混沌状态。而一旦陷入混沌的市场中，博弈双方初始条件的细微变化都会极大地影响最终结果，企业对市场的变化情况不能进行有效的预测。进入混沌市场是企业所不愿面对的情况，此时企业必须进行混沌控制减少市场的不确定性。延迟反馈控制是一种很好的混沌控制法，运用它对陷入混沌状态的系统进行控制，可以使系统重新回到Nash均衡状态。

［1］陈文颖，吴宗鑫.碳排放权分配与碳排放权交易［J］.清华大学学报（自然科学版），1998，38（12）：15-18.

Chen Wenying，Wu Zongxin.Carbon emission permit allocation and trading［J］.Journal of Tsinghua University（Science and Technology），1998，38（12）：15-18.

［2］Lawrence H，Goulder，et al.Impacts of alternative emissions allowance allocation methods under a federal cap-and-trade program ［J］.Journal of Environmental Economics and Management，2010，60（3）：161-181.

［3］陈晓红，王陟昀.碳排放权交易价格影响因素实证研究——以欧盟排放交易体系为例［J］.系统工程，2012，30（2）：53-60.

Chen Xiaohong，Wang Zhiyun.Empirical research on price impact factor of carbon emission exchange：evidence from EU ETS［J］.Systems Engineering，2012，30（2）：53-60.

［4］Kara M，Syri S，Lehtil A，et al.The impacts of EU CO2emissions trading on electricity markets and electricity consumers in Finland［J］.Energy Economics，2008，30（2）：193-211.

［5］Puu T.The chaotic duopolies revisited［J］.Journal of Economic Behavior and Organization，1998，33（3）：385-394.

［6］Agiza H N，Hegazi A S，Elsadny A A.Complex dynamics and synchronization of duopoly game with bounded rationality［J］.Mathematics and Computers in Simulation，2002，58（2）：133-146.

［7］Elabbasy E M，Agiza H N，Elsadany A A.Analysis of nonlinear triopoly game with heterogeneous players［J］.Computers and Mathematics with Applications，2009，57（3）：488-499.

［8］达庆利，闫安.相异成本情形下的耐用品动态古诺模型研究［J］.管理工程学报，2007，21（3）：56-59.

Da Qingli，Yan An.Study of a dynamical Cournot model with durable goods and different costs［J］.Journal of Industrial Engineering and Engineering Management，2007，21（3）：56-59.

［9］潘玉荣，贾朝勇.不同理性双寡头博弈模型的复杂性分析［J］.复杂系统与复杂性科学，2007，14（2）：71-76.

Pan Yurong，Jia Chaoyong.Complex dynamics analysis for a duopoly game with heterogeneous players［J］.Complex Systems and Complexity Sscience，2007，14（2）：71-76.

［10］胡荣.学习效应、有限理性与动态古诺竞争复杂性［J］.复杂系统与复杂性科学，2011，8（4）：44-50.

Hu Rong.Learning effects，bounded rationality and complexity analysis of dynamical Cournot game［J］.Complex Systems and Complexity Science，2011，8（4）：44-50.

［11］姚洪兴，张芳.差异化策略的两组动态古诺模型及其稳定性控制［J］.江苏大学学报（自然科学版），2012，33（3）：364-368.

Yao Hongxing，Zhang Fang.Dynamic model and stability control of heterogeneous decisions in two teams Cournot game［J］.Journal of Jiangsu University（Natural Science Edition），2012，33（3）：364-368.

［12］Dixit A.Comparative statics for oligopoly［J］.International Economic Review，1986，27（3）：107-122.

［13］Puu T.Attractors，Bifurcations and Chaos：Nonlinear Phenomena in Economics［M］.Berlin：Springer，2000.

［14］Pyragas K.Continuous control of chaos by self-controlling feedback［J］.Physics Letters A，1992，170（6）：421-428.

Analysis of Duopoly Game with Bounded Rationality and Carbon Emission Trading

ZHAO Ling-rui，ZHANG Ji-xiang
（College of Economics and Management Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

Improving the Cournot model with bounded rationality，and then applying it to the carbon emission trading market，a duopoly game with bounded rationality and carbon emission trading was established.By using the theory of nonlinear dynamic systems，the existence and stability of the equilibrium point of this model were discussed and some numerical simulations were made.The research results showed that carbon emission trading played an important role in the system.The price of allowances of carbon emission trading and the carbon emission coefficient not only affected the outputs of each firm in the equilibrium point，but also influenced the stability of system.Nash equilibrium of the model can be maintainable by using delayed feedback control method when the model in chaos state.

carbon emission trading；bounded rationality；Cournot model；chaos

F224；X51

A

1672-3813（2013）03-0012-08

2013-01-13

国家自然科学基金（71101071）；国家重点基础研究发展计划（2012CB955802）；江苏省教育厅哲学社会科学基金（2012SJD630086）；中央高校基本科研业务费专项资金资助（NR2010039，NR2013006）

赵令锐（1989-），男，江西吉安人，硕士研究生，主要研究方向为有限理性博弈和企业决策。

（责任编辑 李进）