一类分数阶HIV模型的稳定性分析①

庄科俊

(安徽财经大学统计与应用数学学院应用数学研究所，安徽 蚌埠 233030)

0 引言

传染病学中数学模型的引入，为理解疾病传播机制及其控制策略提供了一个全新的视角[1].Tuck与Wan建立了如下的HIV型种群动力学模型[2]:

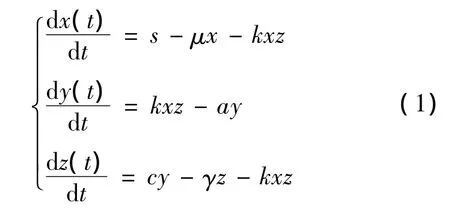
其中x与y分别是t时刻未感染和已感染的CD4+T细胞的数量，z表示t时刻血浆中病毒粒子的数目.系统中所有系数均为正数，s是CD4+T细胞的生成率，μ是人均死亡率，k是CD4+T细胞被病毒的感染率，a是被感染细胞的人均消失率，c为感染细胞与病毒的转化率，而γ则是病毒粒子的死亡率.对系统(1)，已有学者研究其简化系统的动力学性质[3]、同伦摄动解[4].

最近，分数阶微积分引起了众多学者的广泛关注.由于分数阶模型的非局部性、记忆性等性质，分数阶微分方程在生物系统的建模中更加贴切实际，并且出现了一些描述传染病动力学、种群动力学的分数阶模型[5－6].因此，这里将考虑系统(1)的分数阶情形:其中 α ∈ (0，1]，Dα是 α 阶 Caputo微分算子[7].Arafa等人利用广义Taylor公式与同伦分析法，研究了系统(2)的简化模型的解[8].而本文的主要目的在于，研究分数阶系统(2)的平衡点的稳定性，并通过数值模拟验证理论分析的结果.

1 稳定性分析

图1 α=0.95时系统(2)的平衡点E2渐近稳定

系统(2)在平衡点E1处的Jacobi矩阵为

相应的特征方程为

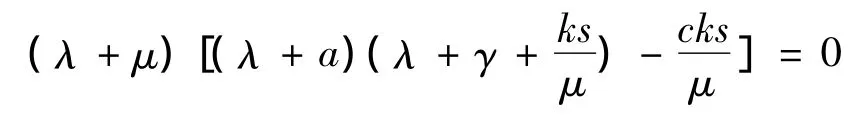
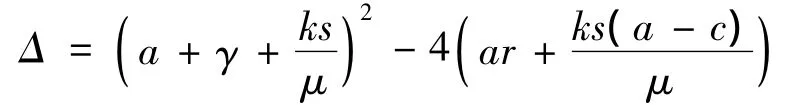
根据分数阶 Routh － Hurwitz准则[9－10]可知，分数阶系统的平衡点稳定当且仅当所有特征根满足|arg(λ)|＞απ/2.通过简单计算不难发现，当arμ＞ks(c－a)时，平衡点E1渐近稳定;否则，E1不稳定.

对平衡点E2，相应的特征方程为:

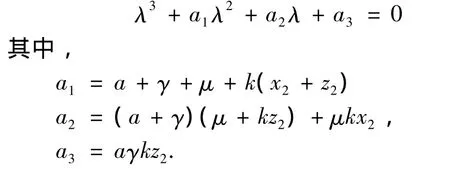
令D(P)=18a1a2a3+(a1a2)2－，根据文献[9－10]中的相关结论，可以得到如下的关于平衡点E2的稳定性结果.

定理

(1)若D(P)＞0，则E2渐近稳定当且仅当a1＞0，a1a2＞a3＞0.

(2)若D(P)＜ 0，a1≥0，a2≥0，a3＞ 0，0.5 ＜ α＜2/3，则E2渐近稳定.

(3)若D(P)＜ 0，a1＞ 0，a2＞ 0，a1a2=a3，0.5 ＜α ＜1，则E2渐近稳定.

(4)若D(P)＜0，a1＜0，a2＜0，α ＞2/3，则E2不稳定.

2 数值例子

根据文献[11]，取 s=0.272，γ =2，μ =0.00136，k=0.00027，a=0.33，c=50，则E2=(49.21，0.6214，15.43)，借助Mathematica计算可得，a1=0.350173，a2=0.0128939，a3=1.86975 ×10－6，则D(P)=1.16422 × 10－5＞ 0，a1a2＞ a3，从而平衡点E2渐近稳定，见图1.

通过之前的分析及数值例子可以发现，当参数在一定情况下，分数阶系统将保持整数阶的稳定性不变.关于分数阶系统(2)的动力学性质，特别是其分支现象，还有待进一步的研究.

[1]F.Brauer，C.Castillo－ Chavez.Mathematical Models in Population Biology and Epidemiology[M].New York:Springer－Verlag，2001.

[2]Henry C.Tuckwell，Frederic Y.M.Wan.Nature of Equilibria and Effects of Drug Treatments in Some Simple Viral Population Dynamical Models[J].IMA Journal of Mathematics in Medicine and Biology，2000，17:311－327.

[3]Henry C.Tuckwell，Frederic Y.M.Wan.On the Behavior of Solutions in Viral Dynamical Models[J].Biosystems，2004，73:157－161.

[4]Mehmet Merdan，ve Tahir Khaniyev.Homotopy Perturbation Method for Solving Viral Dynamical Model[J].Fen Bilimleri Dergisi，2010，31(1):65 －77.

[5]Nuri Ozalp，Elif Demirci.A Fractional Order SEIR Model with Vertical Transmission[J].Mathematical and Computer Modelling，2011，54:1－6.

[6]程媛媛，蒋威.分数阶时滞单种群模型的稳定性[J].佳木斯大学学报(自然科学版)，2012，39(3):468－469.

[7]I.Podlubny.Fractional Differential Equations[M].San Diego:Academic Press，1999.

[8]AAM Arafa，SZ Rida，M Khalil.The Effect of Anti－ viral Drug Treatment of Human Immunodeficiency Virus Type 1(HIV－1)Described by a Fractional Order Model[J].Applied Mathematical Modelling，2012.

[9]E.Ahmed，A.M.A.El－Sayed，Hala A.A.El－Saka.On Some Routh－Hurwitz Conditions for Fractional Order Differential Equations and Their Applications in Lorenz，Rssler，Chua and Chen Systems[J].Physics Letters A，2006，358:1 －4.

[10]Mohammad Reza Faieghi，Hadi Delavari.Chaos in Fractional－order Genesio－ Tesi System and its Synchronization[J].Commun.Nonlinear Sci.Numer.Simulat.，2012，17:731 －741.

[11]AN Phillips.Reduction of HIV Concentration during Acute Infection:Independence from a Special Immune Response[J].Science，271:497－499.