列车隧道交会最不利长度数值模拟研究①
陶泽平, 杨志刚, 陈 羽
(同济大学上海地面交通工具风洞中心,上海 201804)
高速铁路是世界铁路客运发展的方向,随着列车运行速度的提高以及线路中隧道比例的增加,高速列车通过隧道引起的气动效应将直接影响到列车运行安全性、经济性、乘员舒适性以及隧道周边环境,是高铁隧道设计中必须解决的关键技术问题[1].对于列车隧道内交会问题,列车头尾在进入隧道时会形成初始压缩波和膨胀波,加上两车交会引起的交会压力波,各种波在隧道内不断传播、反射与叠加,形成复杂又强烈的压力波动[2].文献[3]建议今后在复线隧道内以会车工况为重点,研究压力波传播规律并确定最恶劣会车工况和相应车内外压力.已有研究表明,与阻塞比和车速不同,隧道长度对瞬变压力的影响呈现明显的非单调性,对隧道设计而言,“最不利隧道长度”的探求很有意义,何种隧道长度使得瞬变压力产生最不利叠加是需要关注的问题[4].王建宇等人[4-6]研究分析了压力波传播、反射和叠加规律,并提出单线隧道相应于压力变化不同情况的“最不利隧道长度”计算图表及公式.王一伟等人[2]通过理论分析研究了隧道压力波形成和峰值影响因素,推导了压力极值对应的最不利隧道长度关于列车长度、运行马赫数的表达式,并通过二维数值模拟方法,对典型工况下不同长度隧道内列车交会进行了计算.
高速列车隧道交会所引起的流动是三维瞬态湍流流动,对压力波的完全描述不仅需要考虑空气的可压缩性、传热和摩擦效应,还应考虑列车头尾部、隧道出入口等处的三维流动.但三维数值模拟的计算量过大,对计算机要求过高;且考虑到隧道交会的控制因素是初始压缩波和初始膨胀波,因此二维数值模拟能够对其进行描述[2].本文通过二维方法,针对两等长等速列车同时进入隧道的简单工况开展不同隧道长度的隧道会车计算,得到列车表面测点的压力变化曲线,并结合图表,对隧道压力波传播规律进行分析,以期对列车隧道交会的最不利隧道长度探究提供帮助.
1 数值模型及计算方法
1.1 数值模型
数值计算中采用某高速列车三节联挂车体二维简化模型,列车几何长度为76.7m,隧道长度系列取 60m,90m,120m,150m,190m,230m,260m,300m,350m,400m,500m.流场采用四边形网格划分,见图1.列车表面及隧道壁面设有边界层网格,经过计算得到壁面大部分在30~150之间,满足计算要求.
计算域布置及边界条件设定如图2,初始时刻列车头部鼻尖距隧道入口50m,通过交界面来实现数据的传递.车身表面设为运动边界,X方向速度分量取为列车运行速度70m/s,其他速度分量为0;根据列车运行方向,定义列车运行后侧边界为压力进口条件,前侧边界为压力出口条件.列车线间距5m,阻塞比为 0.242.

图2 计算域与边界条件
1.2 计算方法
列车与列车、列车与隧道之间的相对运动通过动态分层方法处理.采用瞬态可压缩方法计算,时间步长为0.005s.湍流计算选用Realizable k-ε两方程湍流模型,考虑到流场的压力梯度效应,采用非平衡壁面函数.离散的控制方程组采用压力基求解,压力速度耦合处理方式采用SIMPLE,空间离散格式中压力项采用标准形式,其余采用二阶迎风格式.列车运行一定时间步后开始记录数据.
1.3 测点布置
为了监测列车表面压力变化,以列车1作为监测车,在车身表面布置测点,如图3.其中测点1,8分别位于列车车头、车尾鼻尖.

图3 车身测点布置
2 计算结果分析
2.1 隧道长度对压力波动的影响
目前在国内外高速铁路设计中通常采用特定时间内压力单调变化值来制定舒适度准则和评价压力波动,本文采用国内普遍采用的3s瞬变压力峰值(Δp/3S)及压力最值进行压力波动程度的评估.
图4给出了不同隧道长度下车头测点1和车尾测点8在3 s内瞬变压力峰值Δp.可以看出,对于测点1和测点8,隧道长度分别为230m和350m时,即隧道列车长度比为3和4.5时,压力变化最为剧烈;随着隧道长度的进一步增加,隧道内瞬变压力的变化不大,基本趋于稳定[7].这说明,对车体瞬变压力而言,最不利隧道长度是存在的,且对于不同的列车表面测点,最不利隧道长度有所变化.
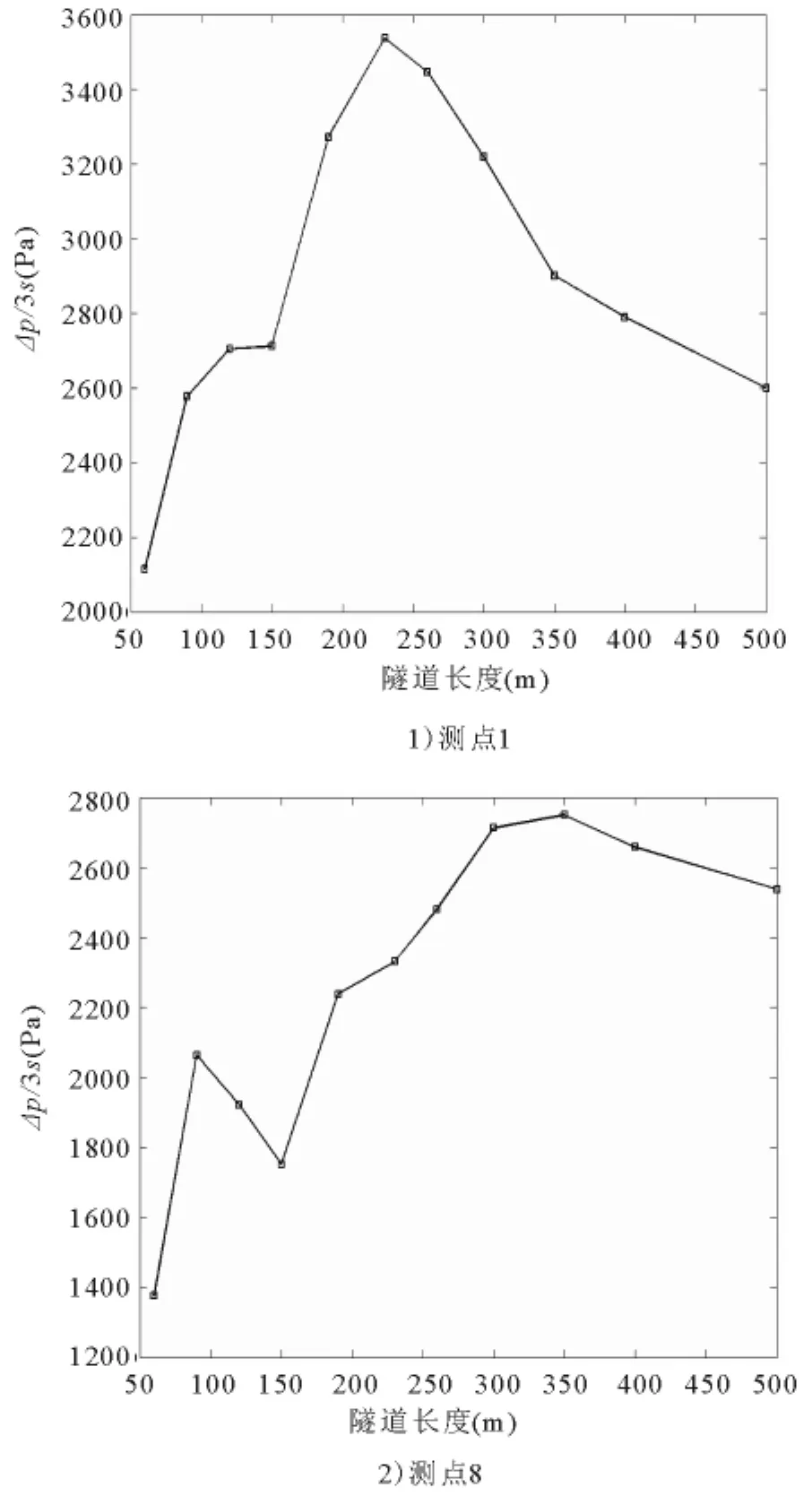
图4 隧道长度与测点压力波动的关系
图5给出测点1、测点3、测点5和测点8的压力最值与隧道长度的关系.不同隧道长度下,测点压力最大值的变化不如测点压力最小值的变化明显,这说明隧道交会过程中通常是负压起主导作用.测点1和测点8的压力最小值分别出现在隧道长度为230m和350m处,这与3s瞬变压力峰值的结果一致.对于压力最小值曲线,隧道长度在60m~190m时,数值变化较为明显,根据文献[2]的结论,此时的隧道长度因处于临界长度中.
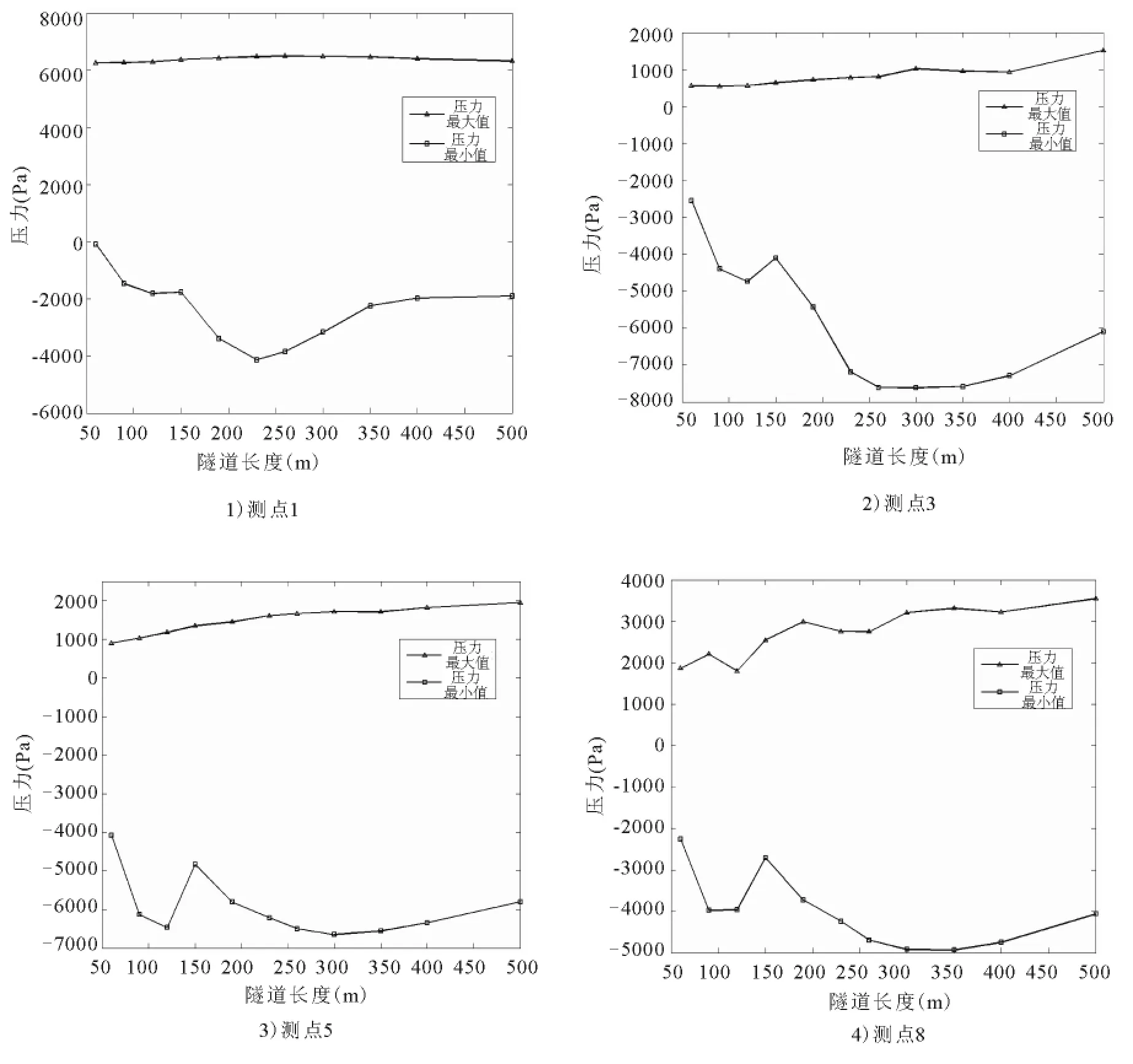
图5 各测点压力最值与隧道长度的关系
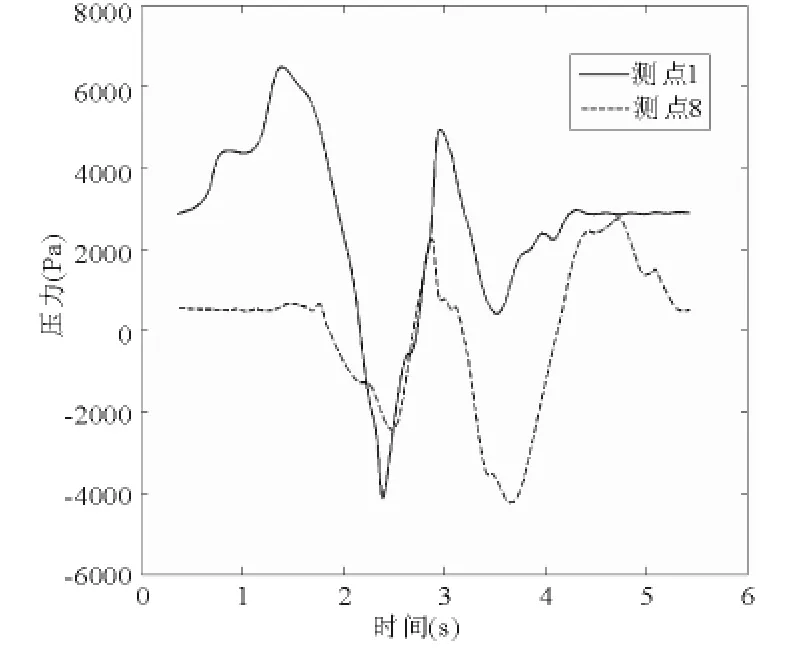
图6 隧道长度230m测点压力变化曲线

图7 隧道长度350m测点压力变化曲线
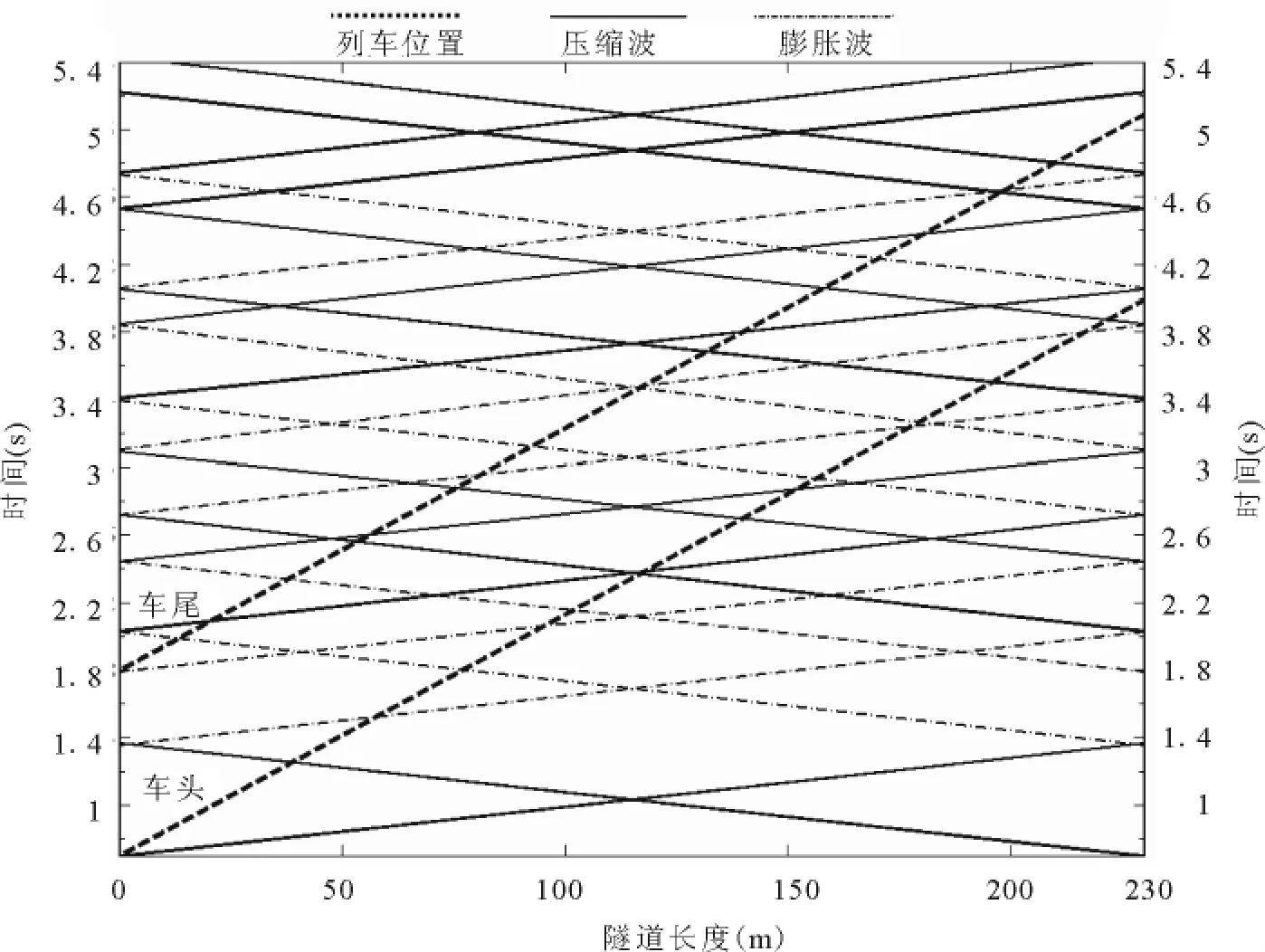
图8 压力波传播与叠加(隧道长度230m)

图9 压力波传播与叠加(隧道长度350m)
2.2 隧道内压力波动的传播与叠加规律
气压波的传播、反射与叠加同隧道长度有着密切关系.前文已指出,相应于瞬变压力急剧程度,车头、车尾测点的最不利压力叠加分别发生在隧道列车长度比为3和4.5时.图6、图7分别给出隧道长度为230m和350m时测点1、测点8的压力变化曲线.为了分析方便,图8、图9对应的给出了隧道长度为230m和350m时隧道内压力波的传播与叠加图(假设波传播速度为声速).下面结合图7和图9就测点8的压力波动进行分析.1.8s时列车1尾车进入,产生初始膨胀波,测点8压力下降;2.6s和2.65s时列车1初始压缩波反射形成的膨胀波和列车2初始膨胀波分别经过测点8,压力下降;在随后的1s时间内,测点8分别经历列车1初始压缩波二次反射形成的压缩波、列车2初始膨胀波反射形成的压缩波、列车2初始压缩波二次反射形成的压缩波及列车1初始膨胀波反射形成的压缩波,压力迅速上升,达到最大值;4.3s时,列车尾车交会,测点8压力产生小幅变化,随着下一轮膨胀波的到来测点8压力达到最小值;之后虽仍有压力波叠加,但由于能量的消耗,测点8压力变化已不再显著.
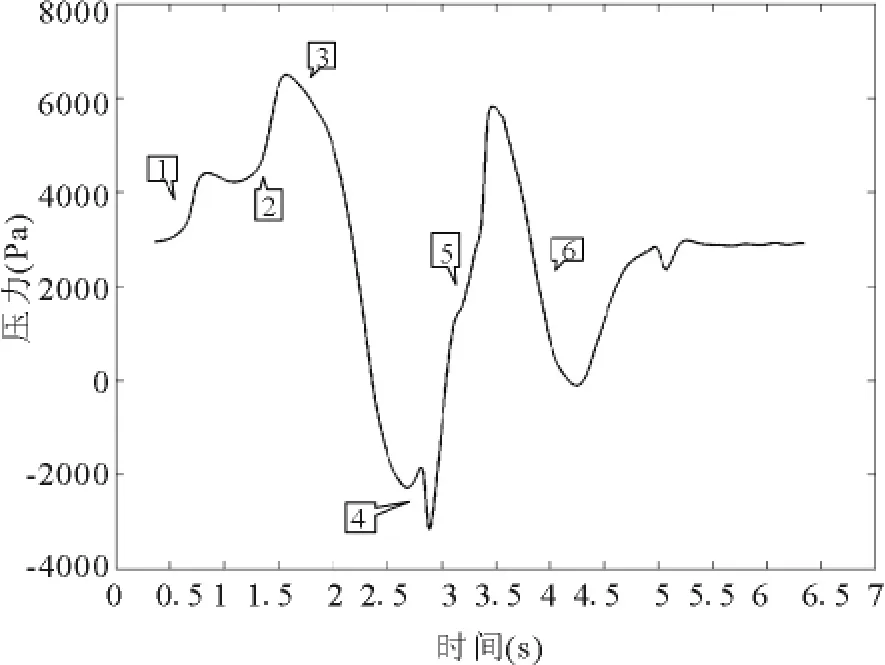
图10 隧道交会测点1压力变化曲线
2.3 压力场演化分析
隧道长度为300m,列车表面测点1的压力变化曲线如图10,对于典型时刻有如下分析(压力云图见图11,标号与图10对应):
(1)0.71s时,列车头部进入隧道,压缩波产生并向前传播.此时,与之交会的对面列车产生的压缩波未到达测点,压力变化幅度不大.
(2)1.56s时,列车2产生的初始压缩波到达测点,压力增大.
(3)1.82s至 2.5s,对面列车产生的初始压缩波传播至隧道出口,经反射形成膨胀波,并与列车尾部进入隧道形成的初始膨胀波叠加.经叠加的压力波经过测点,压力大幅度降低.
(4)2.85s时,两列车在隧道中间交会,测点压力形成先上升后降低趋势,且压力达到最低点.
(5)随着交会的进行,新的压缩波形成并使测点压力逐步上升.
(6)压缩波、膨胀波在隧道内继续传播、叠加、反射,但由于能量的消耗,所引起的压力变化已经不再显著.
3 结论
(1)二维计算表明,相应于瞬变压力急剧程度,车头、车尾测点的最不利隧道长度分别为3倍列车车长和4.5倍列车车长.
(2)车身表面测点压力最大值随着隧道长度的变化不如测点压力最小值相应的变化明显,说明隧道交会过程中通常是负压起主导作用.

图11 隧道交会不同时刻压力云图(隧道长度300m)
(3)本文提出的隧道压力波传播与叠加图有助于准确和方便的分析隧道压力波传播规律.
[1]中国铁道科学研究院.京沪高速铁路综合试验研究分报告之八——高速铁路气动效应试验研究[R].北京:中国铁道科学研究院,2011.
[2]王一伟,杨国伟,黄晨光,王伟.隧道长度对高速列车交会压力波的影响研究[J].中国科学(E辑:技术科学),2012,42(1):82-90.
[3]王潇芹,梅元贵,周朝晖.CRH3高速列车隧道压力波特性浅析[J].兰州交通大学学报,2011,30(1):117 -121.
[4]王建宇,万晓燕,吴剑.隧道长度对瞬变压力的影响[J].现代隧道技术,2008,45(6):1-4 .
[5]王建宇.高速列车隧道空气动力学若干问题探讨[C].中国高速铁路隧道国际技术交流会论文集,2006:74-86.
[6]王建宇.关于高速铁路隧道设计参数问题[J].世界隧道,1998,5:1 -7.
[7]马伟斌,张千里,刘艳青.中国高速铁路隧道气动效应研究进展[J].交通运输工程学报,2012,12(4):25 -32.

