动量轮诊断测点配置与资源占用度成本评价

刘 睿 周 军 李 鑫 刘莹莹

(西北工业大学 精确制导与控制研究所，西安710072)

基于可诊断性的测点配置在卫星设计阶段有着非常重要的意义，直接关系着系统故障检测和诊断的能力.可诊断性主要指当发生一个或多个故障时，系统能检测故障并能识别故障原因的能力，主要包括故障可检测性和故障可分离性［1-2］.当前测点配置的研究大多集中在求解基于优化问题的测点优化配置，需要以传感器的个数、位置、成本和重量为优化目标，以状态可观性、故障可检测性或可分离性为约束条件，建立用于测点配置的优化问题.针对上述优化问题，研究有效的优化求解算法，例如随机搜索法、遗传算法(GA，Genetic Algorithm)、模拟退火(SA，Simulated Annealing)、蚁群算法和粒子群算法、非线性二次规划问题求解等［3-9］.目前在建立优化目标和约束条件的量化指标方面有一定的研究成果，但求解算法比较复杂，且不直观.采用这类方法进行的研究均针对某类系统进行，没有形成统一的步骤，不利于方法的移植.在国内研究比较多的可测试性设计是基于系统功能模型的基础上，通过整合形成一个顶层的测试系统模型的过程，在完成模型建立后，如何在多回路中检测和隔离出具体故障成为难点问题［10］，本文提出的方法也可以对可测试性设计提供借鉴.

Bhushan等人利用DG(Directed Graph)图完成了基于可诊断性的测点配置方案［10-15］，这个方案算法简便直观，在测点配置问题上非常行之有效.本文借鉴Bhushan等人在化工系统中的基于DG图进行诊断测点配置的应用方法完成动量轮的测点配置.Bhushan等人在DG图模型中将回路作为一个节点讨论，而航天器控制系统中存在着大量回路，而且回路内部的可诊断性也受到了极大的关注，因此，本文针对此问题提出了回路进行预处理方案，对方法进行了补充.

基于DG图进行诊断测点配置的方法是一个保守设计方法，可能会得到多个满足可诊断性的测点配置方案，在这些方案中，依照某一优化目标，可以对其进行进一步的筛选，得到相对优化的方案.本文分析上述测点配置所需的成本，包括对系统体积、重量、功耗、处理能力等资源的要求，建立可诊断性与成本之间的分析模型.在此基础上，优选占用资源最小的设计方法，从而实现控制系统故障诊断能力尽可能提高、占用系统资源尽可能少的目的.

动量轮是卫星姿态控制系统重要的惯性执行部件，本文以动量轮为例开展测点配置，完成基于DG图的满足可诊断性的测点配置方法与成本分析评价方法.

1 基于DG图的诊断测点配置

1.1 DG图故障传播模型建立

DG图由若干个节点和若干条支路(即有向边)组成，节点表示变量，支路表示变量之间的关系.

一套动量轮组件由动量轮和动量轮线路盒两台单机产品组成，本文将动量轮分为轮体和电机2个功能模块，将动量轮线路盒分为前级电源变换、加速/减速器、电流控制器、换向开关和换向逻辑、力矩方向变换逻辑和驱动级等6个功能模块.

以各个模块的输出作为测点建立测点集合，对各个测点进行编号.共有17个测点，得到测点集合:

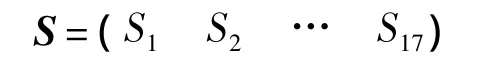
测点编号如表1所示.通过对动量轮故障建模仿真分析，总结动量轮的14种故障模式，得到故障集合:

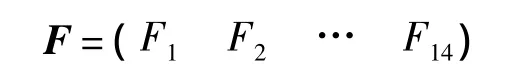
动量轮故障编号如表2所示.

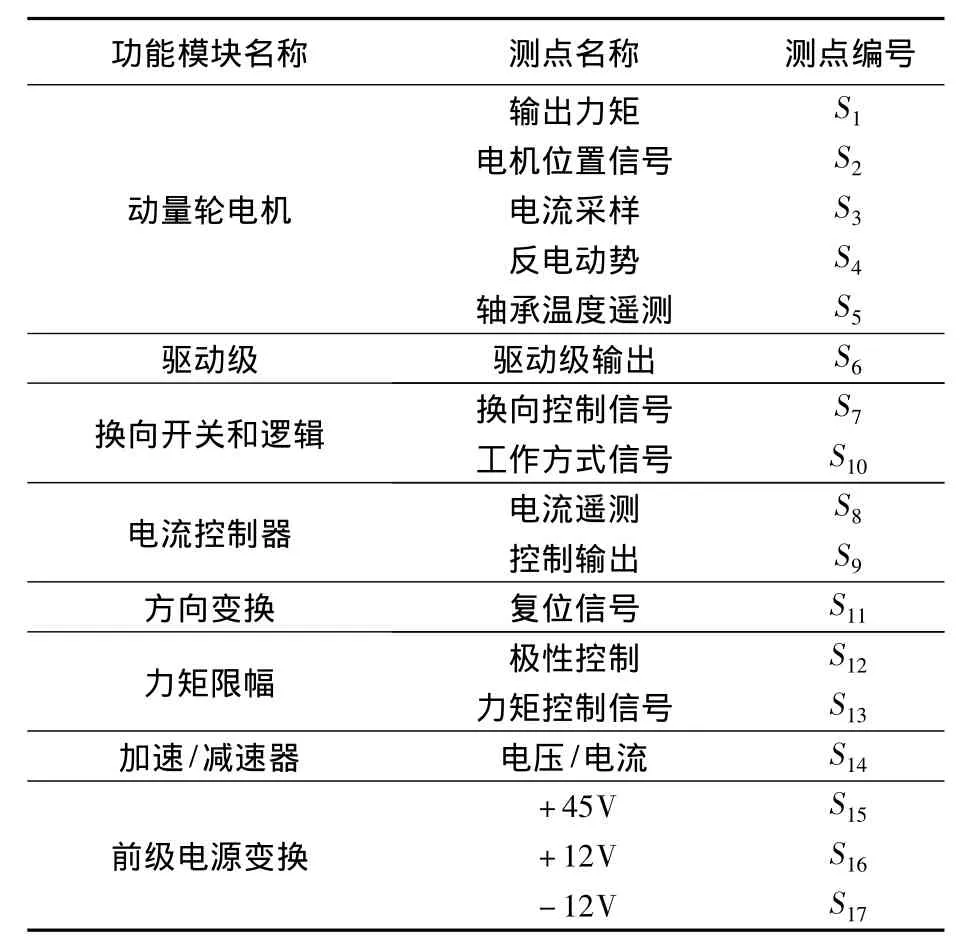
表1 动量轮测点编号Table 1 Sensor identifier of flywheel

表2 动量轮故障编号Table 2 Fault identifier of flywheel

分析不同故障直接影响到的测点，总结动量轮故障与测点的关系，建立故障传播DG图模型如图1所示.在测点配置之前，需要对DG图做预处理.为了建立偶图，需要消除DG图中的回路，回路性质不同，处理方式也有所不同.回路处理规则如下:

1)对于非控制回路，不做处理;

2)负反馈控制回路，将输出反馈模块的有向边断开.

依据以上规则预处理后的DG图如图2所示.

图1 动量轮故障传播DG图Fig.1 DG of fault transmit model of flywheel

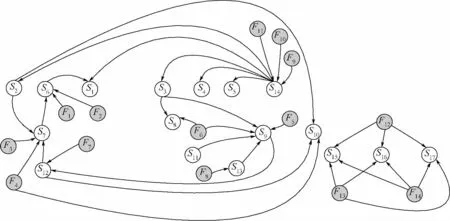
图2 预处理后的动量轮故障传播DG图Fig.2 DG of fault transmit model of flywheel after operation

1.2 偶图建立

对DG图进行预处理以后，所有的回路都被消除，为了建立偶图，偶图由两排节点和有向边组成，第1排表示所有可选测点，第2排表示所有可能故障，用有向边从故障指向与其相关的测点.首先需要生成满足可诊断性要求的根节点，进行如下定义:

1)满足可检测性的根节点.

对每一个故障i，建立集合Ai，Ai中的元素为受到故障i影响的测点.

2)满足可分离性的根节点.

定义:

Bij表示仅与故障i相关的测点集合和仅与故障j相关的测点集合的并集，其中的元素仅能表现故障i或j二者之一.在这些测点中选择关键集合，就保证可以满足可分离性的要求.

将以上生成的满足可检测的根节点和满足可分离的根节点作为偶图的根节点，建立偶图.

2 测点配置算法

定义最终选择的诊断测点为关键测点.定义入度为测点关联的故障节点的个数.基于可诊断性目标采用贪婪算法进行测点配置，即总选择当前状态下入度最大的测点作为关键测点，关键测点选择的步骤如下:

1)选择入度最大的测点，将其作为关键测点，放入关键测点集合，如图3所示，S1与S3测点相关的故障有两个，而S2相关的故障有3个，因此，选择S2测点.

2)判断所有根节点是否被覆盖.若是，测点选择完成，若不是，删除已覆盖根节点与其他测点的连线，如图3所示，图中选择S2测点作为关键测点，用阴影表示，由于其并未覆盖故障根节点F5，因此删去已覆盖根节点 F1，F2，F3，F4与其他关键测点的连线，图中用虚线表示.

图3 关键测点选择举例Fig.3 Example of the key sensor selection

3)回到步骤1)，仅有的F5与S3相关，因此，选择S3，此时，所有根节点均被覆盖，因此，诊断测点可选择为 S2，S3.

由以上方案选择的关键测点集合并不是最优的，基于以下例子可以看出.假设系统建立的偶图如图4所示，按照以上方法，选择入度最大的测点S1为关键测点，并删除已覆盖根节点F1，F2，F3与其他关键测点的连线，根据以上算法，测点S2，S3，S4均需要被选入关键测点集合.显然，S2，S3，S4测点可以覆盖 F1，F2，F3故障，因此，S1测点是多余的.

图4 算法反例Fig.4 Special case of the algorithm

3 测点配置结果

关键测点选择，考虑具体要求，对系统要求必须设置的测点，例如遥测测点，将其设置较高的优先级，在动量轮中，轴承温度遥测测点S5和电流控制器电流遥测S8是必须设置的测点，应该设置较高的优先级，对S5和S8优先处理.

高优先级测点配置完成后，计算所有测点的入度如下:

R=［12，0，0，0，0，12，15，0，12，12，0，15，7，0，7，7，7］可以看出，入度最大为15，但是存在重复，测点S7和测点S12入度均为15，不考虑测点成本等其他因素，认为各个测点没有区别的情况下，按照测点编号的顺序，优先选择测点S7完成一套测点配置方案，如果需要多提供几种测点配置方案以供比较，在配置完成后，可以再返回选择测点S12重新完成一套测点配置方案.

循环时默认顺序选择，首先选择测点S7，关键测点配置选择如下:

Skey1=［1，0，0，0，1，0，1，1，1，1，0，1，1，0，1，0，0］

循环时默认倒序选择，首先选择测点S12，关键测点配置选择如下:

Skey2=［0，0，0，0，1，1，1，1，0，1，0，1，1，0，0，0，1］

以上得到的两种配置结果，第1种选择了9个关键测点，第2种选择了8个测点，这说明了入度相同时，测点选择顺序对结果会有很大的影响.在第1步以后出现的入度相同的测点也有多种选择方案，在计算允许范围内，可以考虑列举多种测点配置方案，综合对比，选择最优方案.

4 资源占用度成本分析

以上测点配置方法会得到多种不同的方案，这时，就需要根据某项优化目标对这些方案进行取舍，成本因素是测点配置必须考虑的一个重要因素，主要需要考虑对系统体积、重量、功耗、处理能力等资源的要求.因此，需要建立成本计算模型.成本与测点的数量、位置等都有关系.引入资源占用度描述成本，其计算受到以下因素的约束:

1)测点配置传感器数量约束.

备选测点向量为 S= ［S1，S2，…，Sn］，传感器配置向量为 X= ［x1，x2，…，xn］，xj为测点 Sj的传感器数量，Q=［q1，q2，…，qn］表示 X 的上限向量，测点传感器数量上限约束如下所示:qj根据系统实际情况确定.

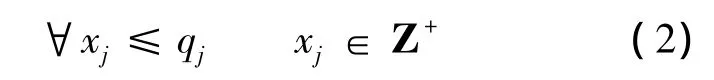
2)测点传感器各项资源要求确定.

考虑增加测点对系统体积、重量、功耗、处理能力等资源的要求，由于体积、重量、功耗等有确定的数值衡量，而测点传感器对处理能力要求没有确定值衡量.因此，在处理无法确定度量的资源占用要求时，将测点分为多个等级，具体等级层数可根据实际情况进行论证，每个等级，为每类测点的资源占用度设以权值，用来描述此类测点资源占用程度.分两类情况:

① 测点占用系统体积 V=［v1，v2，…，vn］，测点配置传感器重量 W=［w1，w2，…，wn］，测点配置传感器功耗 P=［p1，p2，…，pn］，均有确定值描述，因此，按照其资源要求取值即可.

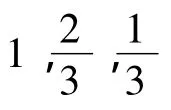
3)测点资源占用度计算.

进行成本比较时，用资源占用度CS表示.

资源占用度需要考虑各种成本的要求，不同成本之间的数值差别很大，如果简单相加会造成某些重要指标被弱化，因此资源占用度用加权平均来表示.资源占用度CS需要满足以下特征:

① CS∈［0 1］.

②CS取值封闭，即∃CS=0且∃CS=1.

因此，本文使用以下公式来计算CS:

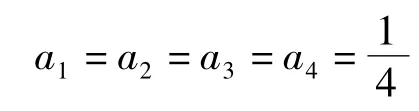
简单举例说明算法应用，第3节选取的两个测点配置方案均满足可诊断性要求，备选测点体积向量为

v=［2.1，3.6，5，8，2.2，6，1.6，7，5.3，4，2，9，1.9，6，7.2，2.9，2］

质量向量为

w=［7.1，9.6，7，8，8.5，9，4.6，6，9.3，5，6，7，4.9，2，8.2，5.9，3］

仅考虑体积和质量约束的资源占用度公式为

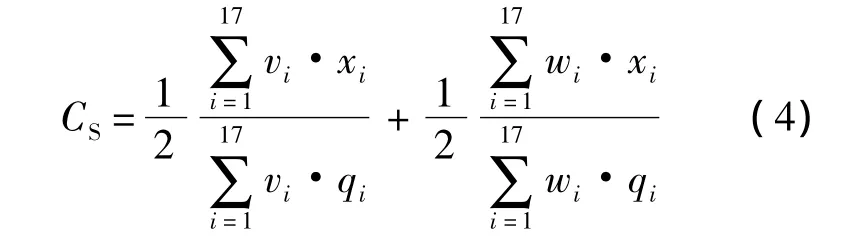
按照第3节两个方案分别将测点矩阵代入计算:

方案1 CS=0.274

方案2 CS=0.203

因此选择方案2为诊断测点配置方案.

5 结论

本文以动量轮为例，基于DG图开展满足可诊断性的测点配置.主要结论有:

1)利用DG图方法完成基于可诊断性的测点配置时，采用贪婪算法可以满足可检测性和可分离性要求，得到的却不是最优测点;

2)提出资源成本占用度的评价指标，可以在测点配置时使得所得到的关键测点满足系统资源成本的限制要求;

3)本文方法基于定性模型展开，可以应用于其他航天器部件的诊断测点配置，具有广泛的适用性.

References)

［1］刘文静，刘成瑞，王南华.故障可诊断性评价与设计研究进展［J］.航天控制，2011，29(6):72-78 Liu Wenjing，Liu Chengrui，Wang Nanhua.Overview of fault diagnosability evaluation and design［J］.Aerospace Control，2011，29(6):72-78(in Chinese)

［2］刘文静，刘成瑞，王南华.基于可诊断性约束的测点优化配置研究［J］.空间控制技术与应用，2011，37(2):1-5 Liu Wenjing，Liu Chengrui，Wang Nanhua.Fault diagnosability constraint based optimistic sensor placement［J］.Aerospace Control and Application，2011，37(2):1-5(in Chinese)

［3］蒋鼎国，张宇林，焦竹青，等.基于QPSCO算法的传感器优化配置［J］.南京理工大学学报:自然科学版，2009，33(4):459-463 Jiang Dingguo，Zhang Yulin，Jiao Zhuqing，et al.Optimal sensor placement based on QPSCO algorithm［J］.Journal of Nanjing University of Science and Technology，2009，33(4):459-463(in Chinese)

［4］杨光，刘冠军，李金国，等.基于故障检测和可靠性约束的传感器布局优化［J］.电子学报，2006，34(2):348-351 Yang Guang，Liu Guanjun，Li Jinguo，et al.Optimal sensor placement based on various fault detectability and reliability criteria［J］.ACTA Electronica Sinica，2006，34(2):348-351(in Chinese)

［5］于保华，杨世锡，周晓峰.一种基于MFM的传感器优化配置方法［J］.振动、测试与诊断，2012，32(2):283-286 Yu Baohua，Yang Shixi，Zhou Xiaofeng.Sensor placement based on MFM［J］.Journal of Vibration，Measurement ＆ Diagnos，2012，32(2):283-286(in Chinese)

［6］胡江华，常新龙，李进军，等.遗传算法在传感器优化配置中的应用［J］.传感器与微系统，2008，27(3):109-113 Hu Jianghua，Chang Xinlong，Li Jinjun，et al.Application of genetic algorithm in optimal sensor placement［J］.Transducer and Microsystem Technologies，2008，27(3):109-113(in Chinese)

［7］ Kotecha P R，Bhushan M，Gudi R D.Design of robust，reliable sensor networks using constraint programming［J］.Computers and Chemical Engineering，2008，32(9):2030-2049

［8］ Duan R X，Ou D X，Dong D C，et al.Optimal sensor placement for fault diagnosis based on diagnosis cost specifications［J］.Journal of Computational Information Systems，2011，7(9)3253-3260

［9］ Yang F，Xiao D Y，Sirish L S.Optimal sensor location design for reliable fault detection in presence of false alarms［J］.Sensors 2009，9(11):8579-8592

［10］路宽，张文杰，解庄.民机电传飞行控制系统测试性设计［J］.航空计算技术，2013，43(2):131-134 Lu Kuan，Zhang Wenjie，Xie Zhuang.Testability design on flight by wire of civil aircraft［J］.Aeronautical Computing Technique，2013，43(2):131-134(in Chinese)

［11］ Raghuraj R，Bhushan M，Rengaswamyan R.Locating sensors in complex chemical plants based on fault diagnostic observability criteria［J］.American Institute of Chemistry Engineering Journal，1999，45(2):310-322

［12］ Bhushan M，Rengaswamy R.Design of sensor network based on the SDG of the process for efficient fault diagnosis［J］.Industrial and Engineering Chemistry Research，2000，39(4):999-1019

［13］ Bhushan M，Narasimhan S，Rengaswamy R.Robust sensor network design for fault diagnosis［J］.Computers and Chemical Engineering，2008，32(4/5):1067-1084

［14］ Mehmet E，Molly H.Model-based solution techniques for the source localization problem［J］.IEEE Transations on Control Systems Technology，2000，8(6):895-904

［15］ Mano R，Raghunathan R，Venkat V.Application of signed digraphs-based analysis for fault diagnosis of chemical process flowsheets［J］.Engineering Applications of Artificial，2004，17(5):501-518