舵叶固定式液压球形关节运动学及性能分析

方守龙 王 亮 丁 帅

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

球面运动机构是一种介于平面机构和空间机构之间的特殊机构，其特点为机构末端的输出轨迹都在一个球面上.球面机构具有结构紧凑、灵活可靠等诸多优点，因此在许多领域得到了广泛的应用，如可用作微创手术机器人［1］、球面点定位设备［2］、机械加工的回转工作台等.近年来，国内外对球面运动机构的构形理论、性能等展开了大量的研究.文献［3］采用了球面三自由度的串联机构研制了机器人的手腕;文献［4］详细阐述了具有运动学各向同性特性的四转轴三自由度球面串联机构;文献［5］介绍了一类球面四杆运动机构，给出了该类机构的构型分类及曲柄存在条件;文献［6］讨论了非对称球面5R并联机构，并且给出了曲柄存在的条件;文献［7］研究了非对称三自由度球面并联机构结构综合问题，讨论了非对称三自由度球面并联机构的类型及达到所需球面运动的机构安装几何条件;文献［8］提出了一类新的3-RRPRR结构的新型球面机构，分析了该类机构的几何构型条件、奇异轨迹及工作空间等.类球铰机构是球面机构的另一热点研究领域，其中最有代表性的是球形电机.文献［9］分析了磁极设计对于球形电机定位转矩的影响;文献［10］介绍了一种具有双气隙特性的多自由度球形电机.鉴于上述机构中串联机构末端刚度小、承载力弱及并联机构工作空间小、奇异位形多、灵活性差等问题，本文提出了一种新型的基于液压驱动二自由度类球铰关节机构，该机构采用了液压驱动，兼有结构紧凑、大负载和大工作空间等特点，有效地弥补了上述串并联机构中存在的不足.

1 机构模型及工作原理

1.1 机构简介

图1为该球形机构的结构简图.该机构由定子、球形转子、超全周转动马达、舵叶、滑轨、码盘等构成，机构的输出部件为球形转子.

图1 球形关节机构示意图Fig.1 Schematic drawing of spherical joint

图2给出了球形关节的内部结构.球形转子与上定子、舵叶间均为球面约束，舵叶轴上安装超全周液压转动马达［11］，所有球面共球心.球形转子位置测量系统采用滑轨支撑框架结构，包括2个圆形滑轨支架、1个滑块和3个码盘，两滑轨安装于下定子且各滑轨转轴过球心.码盘Ⅰ和Ⅱ测量值为X和Y滑轨转角值，码盘Ⅲ测量值为超全周马达输出转角值.图3为舵叶及上定子结构图.

图2 关节内部结构Fig.2 Interior structure of joint

图3 零件示意图Fig.3 Schematic drawing of parts

1.2 坐标系建立

以球心O为原点，分别建立与定子相连的固定坐标系OXYZ和与舵叶及球形转子相连的动坐标系Ox1y1z1和Ox2y2z2，如图4所示.

图4 球形关节坐标系Fig.4 Coordinates of spherical joint

固定坐标系中的X和Y轴分别与X滑轨及Y滑轨的转轴轴线重合(Z轴由右手定则确定);舵叶坐标系中的x1与舵叶两端圆柱面轴线重合，z1轴与Z轴重合;球形转子坐标系z2与转子轴轴线重合，x2轴与初始位置时的x1轴重合.在初始位置，所有坐标系重合(初始位置如图1所示).

1.3 机构驱动描述

该球形关节采用舵叶摆动马达及超全周转动马达进行驱动.如图2所示，舵叶、球形转子和上下定子间构成了两个密封的油腔，由初始位置，当两腔存在压差Δp时，球形转子绕舵叶x1轴摆动γ角，构成了舵叶摆动马达;超全周转动马达初级定叶片［11］嵌于下定子内壁，这样该马达可以带动舵叶绕Z轴转动α角(α为码盘Ⅲ测量值).当超全周马达带动舵叶绕Z轴转动α时，由于舵叶两端圆柱面恒与球形转子接触且两油腔存在压差Δp，使得球形转子绕Z轴旋转α角(如图4所示，∠XOx1=α，∠ZOz2=γ).

两马达需要两套独立的油路进行配油.考虑使配油方式及油路简洁，舵叶摆动马达两油路位于该机构的舵叶轴;超全周马达两油路分别位于舵叶轴及下定子壁(如图2b、图5所示).

图5 马达油路示意图Fig.5 Schematic drawing of motor oil circuit

舵叶摆动马达两油腔由上下定子、舵叶及球形转子4部分构成(图2b).图3中a，c，d处密封分别表示舵叶与球形转子、舵叶与下定子、球形转子与上定子间的密封.

球形转子具有绕x1和Z轴两个转动自由度，这样其末端能够达到以坐标系原点为球心的球面上任意一点，从而球形转子能够实现全方位输出.

2 机构运动学及性能分析

2.1 正解分析

由运动描述可知，球形转子的运动均可分解为绕x1和Z轴的转动，球形转子最终位姿为

式中，γ为舵叶摆动马达转角;α为超全周转动马达转角;Rk(θ)为绕k轴旋转θ角的旋转矩阵［12］.

如图6所示，B和C分别为X滑轨和Y滑轨的中间位置点，D为两滑轨的交点，下面推导滑轨支撑框架位置测量系统中两码盘转角θx，θy与两马达转角γ，α的关系.可将球形转子最终位姿看作沿X滑轨运动的x-y-z欧拉角变换;或者看做沿Y滑轨运动的y-x-z欧拉角变换［12］.

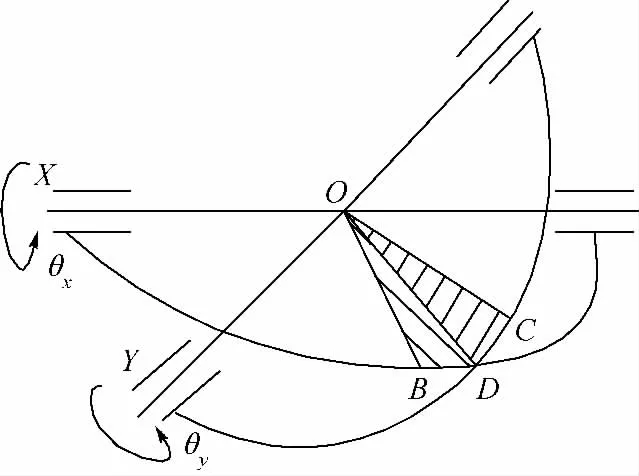
图6 滑轨支撑架示意图Fig.6 Schematic drawing of support frame of slide rail

分别沿X滑轨和Y滑轨变换，球形转子位姿分别如式(2)和式(3)所示.

式中，θx，θy为码盘Ⅰ，Ⅱ转角;ψz，βz为球形转子绕z2轴转角;ψy=∠BOD;βx=∠COD.

由式(1)、式(2)，式(1)、式(3)对应相等，可得

式(4)给出了两码盘转角θx，θy与两马达转角γ，α角的关系.

2.2 逆解分析

将式(4)代入式(1)，消掉γ和α可得以两码盘转角θx和θy表示的姿态矩阵T3.令T3=T，可得

式中，m=tanθx;n=tan θy;atan 2(m，n)为 4 个象限内的反正切函数［12］.

由式(5)可知，逆解有两组，即先转γ角，再转α角;或者先转-γ角，再转π+α角，球形转子都将得到同一位姿.

2.3 奇异位形分析

根据旋量理论［13］，球形转子在固定坐标系OXYZ中的角速度为

式中，s1=［cosα sinα 0］T;s2=［0 0 1］T.

式中，Gv为3×2阶雅可比矩阵:

当γ=0时，机构处在奇异位形，此时超全周马达带动舵叶旋转α时，球形转子末端p点位置不变，即机构失去了一个自由度，如图7所示.此时，舵叶的运动可由码盘Ⅲ进行观测.

图7 关节奇异位形Fig.7 Singular configuration of joint

由于机构设计参数的限制，γ＜π.

2.4 灵巧度评价指标

机构的灵巧度反应了机构的输入与输出之间的传递关系的失真程度，文献［14］定义了机构的角速度各向同性指标:

式中，||||为矩阵Frobenius范数;G+为速度雅可比矩阵广义逆;kG＞1［15］，为了描述方便，通常取1/kG作为机构的灵巧度指标:

1/kG的取值范围为(0，1］，该值越接近1，说明机构各向同性就越好，灵巧度就越高.

3 仿真

3.1 运动分析

由初始位置，假设关节的摆动马达转速为π/40rad/s，超全周马达转速为π/5 rad/s，仿真时间10s.取球形转子末端点p(设=100 mm)为观测点，利用式(1)计算p点在基坐标系中X，Y，Z位置坐标值，在Matlab及Pro/E中的仿真曲线如图8所示;利用式(4)计算两码盘转角θ(单位:(°))，码盘转角在Matlab及Pro/E中仿真图线如图9所示.

图8 p点位置曲线Fig.8 Position curves of point p

由图8、图9可以看出，推导的运动学正解公式及两码盘转角公式在Matlab中仿真与Pro/E中模型运动仿真结果一致，证明了理论分析的正确性.

3.2 机构性能分析

由式(6)～式(9)可求得该机构灵巧度性能指标，如图10所示.

图9 码盘旋转角度曲线Fig.9 Rotation angle curves of code wheel

图10 灵巧度性能指标曲线Fig.10 Dexterity index curve

由图10可知，机构的灵巧度指标取决于摆动马达转角γ，而与超全周转动马达转角α无关.γ越大，灵巧度指标越高;在奇异点位置(γ=0 rad)，机构灵巧度指标接近于0，此时马达输入转角与球形转子末端点位置输出关系严重失真.对该指标的分析可以得到机构良好工作空间为γ≥0.7 rad的区域，此区域内机构灵巧度指标接近且达到最大值，机构各方向运动传递性能类似，有利于该关节控制.

4 结论

1)提出了一种新型的基于液压驱动二自由度球面运动关节，该关节机构采用了液压驱动，可以承受大负载;通过两马达转角的叠加，可以实现球面上任意位置的输出.

2)γ=0 rad时，该机构处于奇异位形状态;γ和α的取值决定了球形转子的最终位姿，其值可由位置测量系统中的码盘进行测量，由此为关节控制创造了条件.

3)在奇异点位置，机构灵巧度指标接近于0.γ越大，灵巧度指标越高.在γ≥0.7 rad的区域，机构灵巧度指标接近且达到最大值，机构各方向运动传递性能类似，有利于该关节控制.

References)

［1］ Lum M J H，Rosen J，Sinanan M N.Optimization of a spherical mechanism for a minimally invasive surgical robot:theoretical and experimenta approaches［J］.IEEE Transactions on Biomedical Engineering，2006，53(7):1440-1445

［2］ Gosselin C M，Caron F.Two degree-of-freedom-spherical orienting device:US，59669［P］.1999

［3］ Gupta K C.Rotability considerations for spherical four-bar linkage with applications to robot wrist design［J］.Journal Mechanisms Transmission Automation in Design，1986(3):387-391

［4］ Chablat D，Angeles J.The computation of all 4R serial spherical wristwith an isotropic architecture［J］.Journal of Mechanical Design，Transactions of the ASME，2003，125(2):275-280

［5］ Chiang C H.On the classification of spherical four-bar linkages［J］.Mechanism and Machine Theory，1984，19(3):283-287

［6］ Kohli D，Khonji A.Grashof-type rotatability criteria of spherical fivebar linkages［J］.Transactions of the ASME，Journal of Mechanical Design，1994，116(1):99-104

［7］ Karouia M，Hervé J M.Asymmetrical 3-dof spherical parallel mechanism［J］.European Journal of Mechanics，A/Solids，2005，24(1):45-47

［8］ Di Gregorio R.A new family of spherical parallel manipulators［J］.Robotica，2002，20(4):353-358

［9］ Jinjun G，Kim D H，Son H.Effects of magnetic pole design on orientation torque for a spherical motor［J］.IEEE Transactions on Mechatronics，2013，18(4):1420-1425

［10］ Lee H J，Park H J，Won S H，et al.Improvements of performance of multi-DOF spherical motor by double air-gap feature［J］.Journal of Electrical Engineering ＆ Technology，2013，8(1):90-96

［11］王亮，胡永杨，方守龙，等.轴向串联式超全周转动液压马达:中国，CN101858369A［P］.2010-10-13 Wang Liang，Hu Yongyang，Fang Shoulong，et al.Tandem axial rotation hydraulic motoroverthe whole week:China，CN101858369A［P］.2010-10-13(in Chinese)

［12］ Critchlow A J.机器人学导论［M］.贠超，译.3版.北京:机械工业出版社，2006:33-36，115-120 Critchlow A J.Introduction to robotics［M］.Translated by Yun Chao.3rd ed.Beijing:China Machine Press，2006:33-36，115-120(in Chinese)

［13］黄真，孔令富，方跃法.并联机器人机构学理论及控制［M］.北京:机械工业出版社，1997:72-88，228-241 Huang Zhen，Kong Lingfu，Fang Yuefa.Parallel robot mechanism and control theory［M］.Beijing:China Machine Press，1997:72-88，228-241(in Chinese)

［14］ Guo X J，Zhu S J.Acceleration and dexterity performance indices for 6-dof and lower mobility parallel mechanism［C］//Proceedings of the ASME Design Engineering Technical Conference.Singapore:ASME，2004，2A:251-255

［15］ Angeles J，López-Cajún C S.Kinematic isotropy and the conditioning index of serial robotic manipulators［J］.The Journal of Robotics Research，1992，11(6):560-571