弯曲滑轨在火箭橇试验弹车分离中的应用*
张 洁,倪晋平,夏洪利,马 群,陈 诚
(1.西安工业大学 光电工程学院,西安710021;2.中国兵器工业试验测试研究院,华阴714200)
火箭橇是以火箭发动机为动力沿专门建造的地面滑轨高速滑行的地面测试设备,是解决武器系统有关速度、加速度的地面试验系统[1-3].导弹战斗部终点毁伤效果的试验验证和考核是火箭橇试验最重要的领域之一.为了精确模拟导弹战斗部的终点毁伤效果,要求战斗部单独作用靶标,需要在着靶前将战斗部与火箭橇车分离,并使两者间距迅速增加,避免橇车与战斗部同时间或者同位置作用靶标,对试验结果产生影响.这就对战斗部火箭橇试验终点弹车分离技术提出了要求.根据导弹战斗部终点毁伤效果火箭橇试验方法和技术流程,弹车分离技术分为两个方面:①战斗部与橇车从连接固定形式分离,使两者从一个整体分成两个整体;②战斗部与橇车空间距离迅速增加,使橇车无法干扰战斗部的飞行姿态,保证战斗部单独撞击靶标.
战斗部与橇车的解锁分离主要是通过爆炸分离装置实现;战斗部与橇车空间距离迅速增加主要是通过战斗部与火箭橇在航向上拉开距离实现.目前,国内外常用的两种较为成熟的方法是水刹车和碰撞拦截.水刹车是应用动量互换原理[4],在战斗部与橇车分离后,利用橇车上安装的刹车装置及布设在分离点后的刹车系统使橇车减速,达到弹车分离的目的;碰撞拦截是在滑轨终点位置的地面上设置碰撞拦截系统,使橇车与碰撞拦截系统发生碰撞,将橇车拦截住,达到弹车分离的目的.因为水刹车需要一定的刹车距离,需要在距离终点较远处释放战斗部,这对保持战斗部的速度和姿态等带来很大的困难,所以在试验中多使用碰撞拦截分离方法.但是,对于结构紧凑、体型小巧的橇车,利用现有方法无法实现弹车分离.因此,针对这类橇车的弹车分离,本文对弯曲滑轨在火箭橇试验弹车分离中的应用展开了研究.
1 弯曲滑轨弹车分离方法
在一些试验中,所用的试验件是等比缩小的模拟件,该类试验件体积小、质量轻,试验所使用的橇车体型较小、结构紧凑.由于该类橇车的空间紧凑性,为了防止战斗部释放后撞击到碰撞拦截系统,不允许通过预置碰撞拦截系统的方式拦截橇车,这就对火箭橇试验终点弹车分离方式提出新的设计要求.本文提出了通过在竖向(即高低方向)上拉开的距离,实现战斗部单独作用靶标的方案,通过研究,这种方案具有可行性.当火箭橇运行到滑轨终端时,战斗部与橇车之间解除约束,战斗部在空气动力作用下惯性飞行,而火箭橇车则需要进入特定装置,实现橇车与战斗部在高低方向上拉开距离,该特定装置为弯曲滑轨,如图1所示.
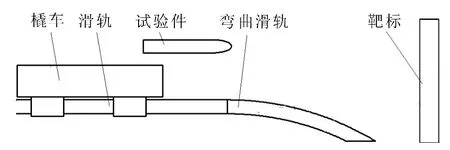
图1 弯曲滑轨弹车分离方法Fig.1 The method of missile-vehicle separation by curved railway track
2 弯曲滑轨的设计
弯曲滑轨就是起点与水平滑轨相切,并按照一定曲率半径折弯,引导橇车偏移靶标的一段特殊滑轨.弯曲滑轨设计的重点是滑轨的曲率半径设计和动响应分析.
2.1 弯曲滑轨半径设计
在弯曲滑轨弹车分离过程中,弹车分离装置所受到的力主要来自橇车在弯曲滑轨上滑行时的振动过载以及橇车的离心力作用.橇车在弯曲滑轨上滑行时的振动过载与滑轨弯曲半径没有必然关系,因此在弯曲滑轨半径设计时需要考虑橇车的离心力作用.离心力计算公式为
式中:M为橇车质量;V为橇车在弯曲滑轨上的滑动速度;R为弯曲滑轨弯曲半径.
已知弯曲滑轨在法线方向上所能承受的许用作用力为[F],则

同时,橇车通过在弯曲滑轨的约束滑行,目的是为了使试验件单独作用于靶标,橇车无法撞击靶标,如图2所示.
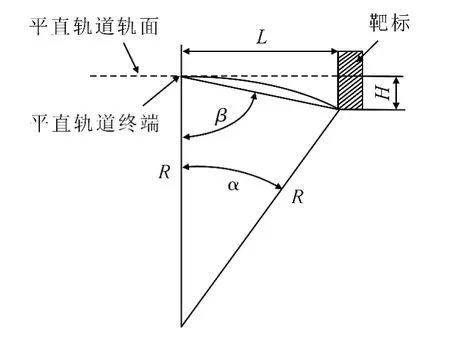
图2 弯曲滑轨半径计算示意图Fig.2 Schematic diagram for calculation of curved railway track radius
火箭橇试验中靶标距滑轨终端距离远大于靶底距滑轨平面高度,即H≪L;另外,为减小弯曲滑轨所承受的离心力,其曲率半径一般设计很大,可认为Hcosα≈H,得出R的表达式为

根据弹车分离目的和要求,实际设计时应该为

综上所述,根据式(2)和式(4)可以得出弯曲滑轨半径的取值范围为

如某型火箭橇试验,橇车质量为50kg,分离时速度为200m·s-1,弯曲滑轨在法线方向上所能承受的许用作用力为2.0×105N,靶标距轨道终点距离为4m,滑轨轨面与靶标下表面间距为0.7m.根据已知条件,计算可得弯曲滑轨半径的取值范围为10m<R<11.1m,综合考虑弯曲滑轨的受力能力和弹车分离的目的,可以设计弯曲滑轨半径为11m.
2.2 弯曲滑轨动响应分析
设计的弯曲滑轨还要进行强度校核计算.以某战斗部火箭橇试验为例,通过强度校核确定弯曲滑轨能否完成在特定速度条件下弹车分离.橇车在弯曲滑轨上的运动是一个复杂的过程,现阶段还没有理论公式或经验公式来支持弯曲滑轨的强度效核,只能通过软件对其进行仿真分析.主要分析橇车在通过弯曲滑轨时对滑轨的摩擦和挤压是否超过了滑轨材料的应力极限[5-7].本文将采用 ANSYS LS/DYNA对其进行刚强度和变形分析.
对弯曲滑轨进行运动学仿真分析时,首先将橇车建立为刚体,赋予橇车质量;滑轨建立为弹塑性体,赋予材料属性.对分析实体划分网格,有限元网格划分是有限元前处理的关键技术,使用全自动网格划分只能实现四面体网格的划分,但六面体网格与四面体网格相比具有单元数少、计算效率高、计算精度好等数值优势[8-9].因此,需要尽可能将仿真分析的几何对象划分成六面体网格.以某火箭橇试验弹车分离模型为例,在网格划分时采用体扫掠法完成六面体单元网格的生成,将分析对象实体尽可能的分成规则的几何部分,并使划分后的不同部分接触面的网格节点相连,网格划分如图3所示.
网格划分后,对滑轨底面进行固定约束,将火箭橇车和滑轨之间设置为自动接触,并给予火箭橇车一定的滑行速度V,进行仿真分析.在分析橇车与滑轨运动过程中,由于橇车滑靴运动与滑轨相互摩擦和冲击,会产生许多变形较大的应力点.根据仿真结果,将滑轨上4个应变最大区域的单元截面进行重点分析.
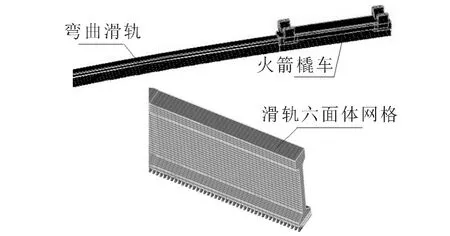
图3 仿真实体六面体网格划分Fig.3 Hexahedral mesh generation of simulation entity
滑轨所用材料为高强度合金钢,其抗压强度为1.57×109Pa,破坏强度为4.0×109Pa.当滑轨所受应力σ大于1.57×109Pa时,滑轨会发生扭曲变形;当滑轨所受应力σ大于4.0×109Pa时,材料强度失效,滑轨会发生破坏、断裂等现象.
1)t=0.001 7s时的滑轨应力如图4所示.由图4可知,在0.001 7s时所选A区域单元的整体应力达到峰值,有80%的单元应力小于1.5×109Pa,只有不到10个单元的应力超过4.0×109Pa,说明这10个单元已经破坏失效,但滑轨整体不会受到影响.
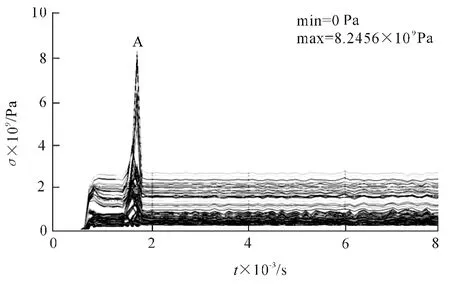
图4 t=0.001 7s时的滑轨应力Fig.4 The stress of railway track at t=0.001 7s
2)t=0.002 3s时滑轨应力如图5所示.由图5可知,在0.002 3s时所选B区域单元的整体应力达到峰值,但有90%的单元应力小于1.5×109Pa,只有4个单元的应力超过4.0×109Pa,说明这4个单元已经失效,但弯曲滑轨整体不会破坏.

图5 t=0.002 3s时的滑轨应力Fig.5 The stress of railway track at t=0.002 3s
3)t=0.003 9s时的滑轨应力如图6所示.

图6 t=0.003 9s时的滑轨应力Fig.6 The stress of railway track at t=0.003 9s
由图6可知,在0.003 9s时所选C区域单元的整体应力达到峰值,有90%的单元应力小于1.5×109Pa,只有2个单元的应力超过4.0×109Pa,说明这2个单元已失效,滑轨整体不会破坏.
4)t=0.004s时的滑轨应力如图7所示.由图7可知,在0.004s时所选D区域单元的整体应力达到峰值,但有85%的单元应力小于1.5×109Pa,只有不到10个单元的应力超过4.0×109Pa,说明这些单元已经失效,但滑轨整体不会破坏.
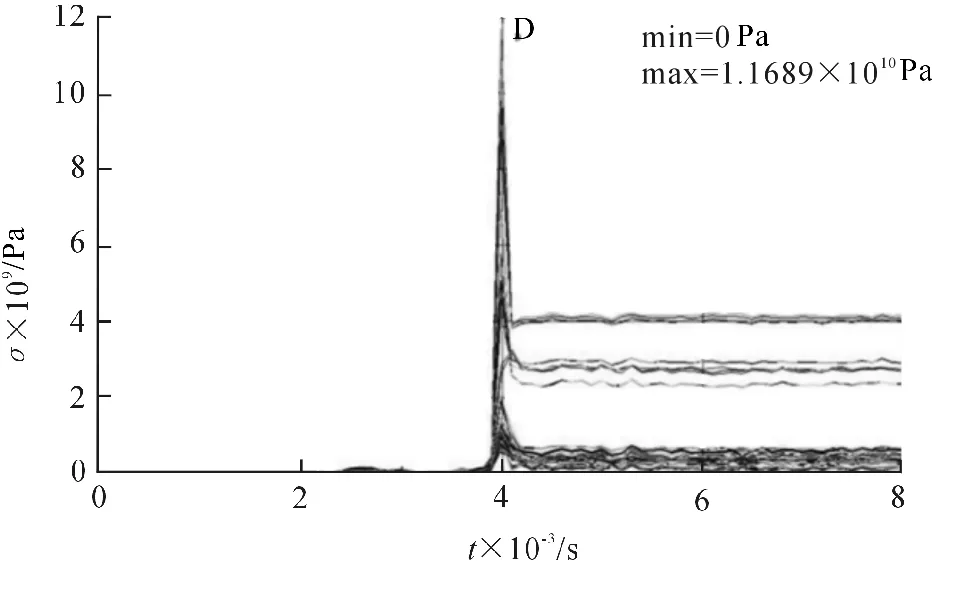
图7 t=0.004s时的滑轨应力Fig.7 The stress of railway track at t=0.004s
橇车在弯曲滑轨上滑动时,需要考虑滑轨是否会发生破坏及其变形情况,图8为在滑轨上选取4个最大位移点的X、Y和Z三个方向的位移(s)-时间(t)历程图,由仿真结果可以看出,滑轨在三个方向上的位移均未超过0.5mm,说明在整个运动过程中,滑轨上端面的变形较小,可以忽略不计.

图8 弯曲滑轨不同点位移变化情况图Fig.8 The map of displacement changes in different regions on curved railway track
经过弯曲滑轨运动学仿真分析可知,此模型中的弯曲滑轨设计合理,能够满足在此橇车质量范围和本试验速度范围内火箭橇试验的弹车分离.
3 结 论
本文提出在垂直滑轨方向上实现弹车分离的方案,并对弯曲滑轨参数设计进行研究,使火箭橇车在弯曲滑轨上限位滑行,实现战斗部与橇车的分离.通过对某型火箭橇试验使用弯曲滑轨弹车分离进行仿真计算,得出结论为
1)弯曲滑轨能够满足某型火箭橇试验弹车分离需求.
2)使用弯曲滑轨实现弹车分离对试验橇车的质量和试验速度有一定的要求,受到滑轨材料力学性能的限制,橇车质量过高或试验速度过快可能导致弯曲滑轨发生断裂,无法实现弹车分离.
[1] 景建斌,赵卫星.火箭橇试验[J].测试技术学报,2012,26:82.JING Jian-bin,ZHAO Wei-xing.The Rocked Sled Test [J].Journal of Test and Measurement Technology,2012,26:82.(in Chinese)
[2] 赵继波,赵峰,谭多望,等.火箭橇加载试验技术研究[J].爆炸与冲击,2007,27(6):572.ZHAO Ji-bo,ZHAO Feng,TAN Duo-wang,et al.Research on Load Technique for Rocket Sled[J].Explosion and Shock Waves,2007,27(6):572.(in Chinese)
[3] 王健,吴军基,陶钢.火箭橇轨道不平顺功率谱密度分析[J].弹道学报,2008,20(4):81.WANG Jian,WU Jun-ji,TAO Gang.Analysis on Power Spectrum Density of Rocket Sled Rail Irregularity[J].Journal of Ballistics,2008,20(4):81.(in Chinese)
[4] 余元元.双轨火箭滑车高速水刹装置研究[D].南京:南京航空航天大学,2008.YU Yuan-yuan.Design and Analysis of High-Speed Water-Brake Device in Double-Track Rocket Sled Test[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2008.(in Chinese)
[5] 王健.高速火箭橇——轨道系统耦合动力学研究[D].南京:南京理工大学,2011.WANG Jian.The Research for Coupled Dynamics of High Speed Rocket Sled-Track Systems[D].Nanjing: Nanjing University of Science and Technology,2011.(in Chinese)
[6] 张立乾,邓宗才,郭富民,等.滑橇高速运动动态效应与滑轨平顺度的关系研究[J].弹道学报,2011,23(2):103.ZHANG Li-qian,DENG Zong-cai,GUO Fu-min,et al.Study on Relation of Slide-Rail Regularity and High-speed Movement Dynamic Response of Sled[J].Journal of Ballistics,2011,23(2):103.(in Chinese)
[7] 846th Test Squadron.Holloman High Speed Test Track Design Manual[R].USA:Holloman AFB,2005.
[8] 毕运波.扫掠体六面体网格生成算法研究[J].浙江大学学报:工学版,2007,41(5):726.BI Yun-bo.Hexahedral Mesh Generation Algorithm of Swept Volume[J].Journal of Zhejiang University:Engineering Science,2007,41(5):726.(in Chinese)
[9] 向华平.基于边界拓扑转化的四面体与六面体网格动态连接技术[J].安徽大学学报:自然科学版,2011,35(2):43.XIANG Hua-ping.A Connective Technology Between Hex and Tetra Based on Topo Translation[J].Journal of Anhui University: Natural Science Edition,2011,35(2):43.(in Chinese)

