锻造操作机大车行走机构的单神经元自适应PID控制＊

王昕炜，苗荣霞

（西安工业大学 电子信息工程学院，西安710021）

锻造操作机是实现锻压机联动作业的辅助设备，对提高锻件质量和实现锻造自动化起到关键作用．锻造操作机20世纪60年代最早出现在欧美国家，早期的锻造操作机采用完全机械的传动方式和控制方法，其结构简单，功能单一，难以完成较为复杂的锻造工艺［1］．70年代随着液压技术的发展，出现了机械传动与液压控制的混合型和全液压系统的锻造操作机，其功能完善，控制灵活，结构简单，工作平稳且抗振，易于控制．随着计算机技术的发展，90年代出现了电控锻造操作机，由于计算机控制特有的优势，使得新型锻造操作机具有更高的运行速度、柔性，控制也更为稳定、可靠，已成为锻造行业主要发展的操作机形式［2-3］．

PID控制算法是最早发展起来的控制策略之一，其算法简单、直观、设计使用简单方便，被广泛应用于锻造操作机控制系统［4］．20世纪50年代，前苏联学者Utkin和Emelyanov提出了变结构PID控制的概念，此后各国学者开始研究变结构PID控制系统，由规范空间扩展到一般的状态空间．谭宝成、王大为［1］通过设计基于在不同的偏差情况下P，PI，PD分段控制的变结构PID控制器，把变结构PID控制算法引入到锻造操作机控制系统中．变结构PID控制系统能够克服系统的不确定性，对干扰和未建模动态具有很强的鲁棒性，尤其是对非线性系统的控制具有良好的控制效果．变结构PID控制信息简单的处理将导致系统的控制精度降低和动态品质变差．若要提高精度就必须增加量化级数，导致规则搜索范围扩大，降低决策速度，甚至不能进行实时控制［1，5］．1974年，英国的E．H．Mamdani首次根据模糊控制语句组成模糊PID控制器，并将它应用于锅炉和蒸汽机的控制，获得了成功．这一开拓性的工作标志着模糊PID控制论的诞生．陈铂金、徐明昊［3］结合模糊PID控制算法，并建立相应的模糊控制规则表，把模糊PID控制算法应用到锻造操作机控制系统中．模糊PID控制具有不依赖被控对象的精确数学模型，简化了系统设计的复杂性的特点．但是模糊PID控制的设计尚缺乏系统性，这对复杂系统的控制难以奏效．难以建立一套系统的模糊控制理论，以解决模糊控制的机理、稳定性分析、系统化设计方法等一系列问题［3-4］．近年来，专家自整定PID控制已广泛应用于现代工业过程控制，它克服了设计缺乏系统性，对复杂系统的控制难以奏效等缺点，针对工业对象本身的时变性与不确定性以及现场干扰的随机性，要求控制器采用不同形式的开环与闭环控制策略，并能通过在线获取的信息灵活地修改控制策略或控制参数，以保证获得优良的控制品质．同时，专家自整定PID控制完全凭经验进行，对于如何保证控制系统的稳定性和鲁棒性问题还有待解决［6］．

针对锻造操作机控制系统的非线性、惯量大等问题，文中通过建立锻造操作机大车行走机构动力学模型，提出单神经元自适应PID控制算法，并对其进行了仿真，以期实现锻造操作机行走机构运动控制．

1 动力学模型的建立

1．1 锻造操作机工作原理

对锻造操作机各个机构的控制包括大车的行进、钳架水平及俯仰、钳架旋转、夹钳旋转、夹钳伸缩以及夹持力的调整等动作．锻造操作机行走机构采用两组液压马达在大车两侧进行同步驱动，其中液压马达的角度、速度以及旋转方向由电液比例方向阀来控制，以此来驱动大车的行走［7］．锻造操作机采用框架式机械结构，通过预紧螺栓现场安装，便于运输和安装．整个锻造操作机由大车、夹钳、钳杆等机械装置及液压和电气控制系统组成，可以配合6 000t锻造水压机在手动、半自动和自动三种工作模式下，完成锻造的整个锻造工艺要求［8］．

1．2 模型的建立

大车行走机构的主要功能是用来实现锻造操作机大车的前进和后退，锻造操作机夹持锻件锻造时的进给和回程等一系列动作，一般分为空载和夹持锻件进给两种工况，空载走动时，大车的行走速度快，液压系统的流量大；用来夹持锻件时，系统的负载功率大，要求行走的位置精度高，从而动态响应快［9］．

大车行走机构的电液比例阀负载流量方程表达式为

式中：Qp为负载的流量 ；xv为阀芯的位移；pl为负载的压降；kq为流量的增益；kc为流量-压力系数．

液压马达腔的流量连续表达为

式中：Dm为液压马达的理论排量（m3·rad-1）；θm为液压马达轴的转角（rad）；Ctm为液压马达的总泄露系数（m5·（N·s）-1），其中Ctm＝Cim＋0．5Cem；Cem为液压马达的外泄露系数（m5·（N·s）-1）；Cim为液压马达的内泄漏系数（m5·（N·s）-1）；Vm为马达腔和阀间的连接管道及阀腔总容积（m3）；βe为系统的综合弹性模量（N·m2）．

假如忽略马达轴上非线性负载和马达腔内油液的质量，则由牛顿第二定律可以得到液压马达的扭矩和惯性力、弹簧力、阻尼力以及任意的外负载间的力矩平衡方程表达式为

式中：Tl为作用在马达轴的任意外负载的扭矩（N·m）；Tg为液压马达产生的理论扭矩（N·m）；J为液压马达轴和负载折算到马达轴的总的惯量（m·N·s2）；Bm为负载和液压马达的粘性阻尼系数（m·N·s·rad-1）；G为弹性负载的扭簧刚度（N·m·rad-1）．

参数Dm和Ctm会随着马达轴的转角的位置改变而发生改变．为了简化分析，一般取平均理论排量Dm和平均泄露系数Ctm．

假设从液压马达的转角到大车行走位移的传动比为im，得到大车行走的位移方程表达式为

其中xm为大车行走的位移．

该系统的四个基本方程均为线性方程，通过解方程组，我们可以得到大车行走的位移xm对于阀芯位移xv的传递函数为

为方便建模，将比例阀位移对其控制电压ud的传递函数定义为

式中：ωd为比例阀阀芯自振频率；ξd为比例阀阻尼比．

2 单神经元自适应PID算法

由于对锻造操作机的稳定性要求高和锻造过程冲击力的存在，在操作机设计时应该考虑机体本身顺应性的能力，所以锻造操作机机体本身的质量较大．由于操作机质量较大，所以在它启动、加速和停止的时候惯量和滞后均比较大．在综合考虑了锻造操作机运动特性之后，决定把单神经元PID控制算法加入到锻造操作机控制系统中［10］．

单神经元PID的控制器的结构框图如图1所示．假设图1中的转换器的输入为yr（k）和输出y（k）；神经元学习控制所需要的状态量x1（k）、x2（k）、x3（k）为转换器的输出，关系式为

其中z（k）为其性能指标．图1中的K为神经元的比例系数，K＞0．神经元一般通过关联搜索来产生控制信号，即

其中ωi（k）对应于xi（k）的加权系数．

图1 单神经元自适应PID控制结构Fig．1 Single neuron adaptive PID control structure

单神经元自适应PID控制器通过对加权系数的调整来实现自适应、自学习功能．加权系数的调整可以采用不同的学习规则，从而构成不同的控制算法［11］．

锻造操作机控制系统采用有监督Heb学习算法的单神经元自适应PID控制器，考虑到加权系数ωi（k）应和神经元的输入、输出和输出偏差三者的相关函数有关，因此在采用有监督Hebb学习算法时有

式中：vi（k）为递进信号，随过程进行逐渐衰减；z（k）为输出误差信号，z（k）＝yr（k）-y（k）＝e（k）；η为学习速率，η＞0；c为常数，0≤c＜1．

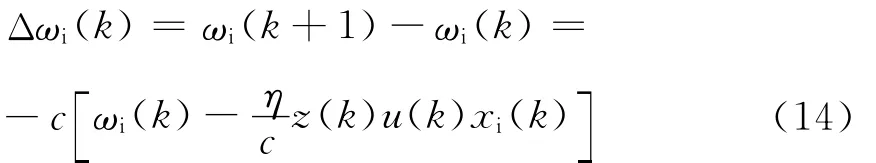
若式（14）各函数存在，则对ωi（k）求偏微分有

式（16）说明加权系数ωi（k）的修正是按照函数fi（k）对应于ωi（k）的负梯度方向进行搜索．为保证这种单神经元自适应PID控制学习算法的收敛性和鲁棒性，将上述学习算法进行规范化处理后可得

式中：ηp，ηi，ηd分别为积分、比例、微分系数的学习速率．对积分、比例和微分分别采用了不同的学习速率ηp，ηi，ηd，以便对不同的权系数分别进行调整．神经元比例系数K的选择非常重要．K越大，则快速性越好，但超调量大，甚至可能使系统不稳定．当被控对象时延增大时，K值必须减少，以报系统稳定．K值选择过小，会使系统的快速性变差［12］．综合考虑，本系统选择K为0．15．

3 仿真及分析

根据锻造操作机液压系统的特性，模拟锻造操作机夹持5t锻件行走情况，有关参数设定为

TL＝150kN·m．代入式（5），即可得到大车行走位移对阀芯位移的传递函数为

系统中比例阀的频率响应为5Hz，因此ωd＝31．4rad·s-1，ξd取经验值0．5，得到阀芯位移对输入控制电压的传递函数为

基于单神经元控制器的构造和锻造操作机的位置控制系统传递函数，运用Matlab／Simulink建立大车行走机构控制系统结构如图2所示，经仿真得出该系统在传统PID控制方式和单神经元自适应PID控制方式下的阶跃响应曲线图，如图3～4所示．

图2 单神经元自适应PID控制系统仿真模型框图Fig．2 Simulation model of single neuron adaptive PID control system

图3 传统PID控制作用下的单位阶跃响应曲线图Fig．3 Step response curve of traditional PID control

图4 单神经元自适应PID控制作用下的阶跃响应曲线图Fig．4 Step response curve of single neuron adaptive PID control

从图3～4的阶跃响应仿真结果可以看出，采用传统PID控制时产生了很大的超调量，振荡幅度较大，并且系统在8s之后才能进入稳定运行状态；采用单神经元自适应PID控制时，超调量低于3s，小于传统PID临界超调量，避免了传统PID控制所产生的超调量超临界问题，大车在3s之后达到匀速运行状态，大车行走机构响应加速度达1 000mm·s-2，速度调整误差为±5mm·s-1，大车行走重复定位误差小于±10mm．

4 结 论

文中通过对锻造操作机大车行走机构进行系统建模，且用自适应方法调节比例、积分、微分控制参数，提出了单神经元自适应PID控制算法，实现了锻造操作机大车行走机构的单神经元自适应PID控制．通过仿真，得出结论为

1）采用单神经元自适应PID控制算法，在不同工况下锻造操作机大车行走机构在3s之后达到匀速运行状态，大车行走机构响应加速度达1 000mm·s-2，速度调整误差为±5mm·s-1，大车行走重复定位误差小于±10mm．

2）当神经元比例系数K值取为0．15时，大车行走机构响应快速性和稳定性达到最优值，大车行走机构运动精度和重复定位精度优于其他取值．

3）通过调整积分微分的切换参数，将比例积分环节与比例微分环节相互独立分段使用，避免了锻造操作机PID控制时超调量超临界值，且运动控制输出振荡幅值得以限定．

［1］ 谭宝成，王大为，俞开文．变结构PID在锻造操作机控制系统中的应用［J］．西安工业大学学报，2009，5（29）：466．TAN Bao-cheng，WANG Da-wei，YU Kai-wen．Variable-Structure PID Control in Forging Manipulator ［J］．Journal of Xi’an Technological University，2009，5（29）：466．（in Chinese）

［2］ 余发国，高峰，郭为忠，等．锻造操作机的回顾与展望［C］／／中国机构与机器科学应用国际会议论文集．上海：上海交通大学，2007：12．YU Faj-guo，GAO Feng，GUO Wei-zhong，et al．Retrospect and Prospect of Forging Manipulator［C］／／Chinese Institutions and Machine Science Applications International Conference Proceedings．Shanghai：Shanghai Jiaotong University，2007：12．（in Chinese）

［3］ 刘一鸣，刘伟，花志远，等．基于模糊PID的电喷天然气发动机空燃比控制策略研究［J］．内燃机工程，2012，6（33）：14．LIU Yi-ming ，LIU Wei，HUA Zhi-yuan，et al．Research on Air-Fuel Ratio Control of Electron-Controlled CNG Engine Based on Fuzzy PID［J］．Chinese Internal Combustion Engine Engineering，2012，6（33）：14．（in Chinese）

［4］ 徐明昊．600kN／1500kN·m锻造操作机控制系统研究［D］．武汉：华中科技大学，2011．XU Ming-hao．Study on Control System of the 600 kN／1 500kN·m Forging Manipulator［D］．Wuhan：Huazhong University of Science and Technology，2011．（in Chinese）

［5］ 武艺泳，陈铁军，罗勇．基于改进型单神经元PID的热牵伸辊温控系统［J］．纺织学报，2013，7（34）：126．WU Yi-yong，CHEN Tie-jun，LUO Yong．Temperature Control System of Heated Draw Roll Based on Improved Single-Neuron PID［J］．Journal of Textile Research，2013，7（34）：126．（in Chinese）

［6］ 任俊杰．基于PLC的单神经元PID控制器的设计与实现［J］．制造业自动化，2012，7（34）：11．REN Jun-jie．Design and Implementation of Single Neuron PID Controller Based on PLC ［J］．Manufacturing Automation，2012，7（34）：11．（in Chinese）

［7］ 孙旭东，王卫红．改进单神经元PID控制器在伺服系统中的应用［J］．系统仿真学报，2006，8（18）：880．SUN Xu-dong，WANG Wei-hong．Application of Improved Single Neuron PID in Servo System ［J］．Journal of System Simulation，2006，8（18）：880．（in Chinese）

［8］ 李晓宁，刘洋，叶小龙，等．基于单神经元PID的永磁同步 电 机 解 耦 控 制 ［J］．电 力 电 子 技 术，2013，9（47）：58．LI Xiao-ning，LIU Yang，YE Xiao-long，et al．Decoupling Control of PMSM Based on Single Neuron PID ［J］．Power Electronics，2013，9（47）：58．（in Chinese）

［9］ LASCU C，BOLDEA I．A Modified Direct Torque Control for Inductionmotor Senserless Drive［J］．IEEE Transon Industrial Electronics，2004，51（4）：785．

［10］ WANG X S，PENG G Z．Modeling and Control for Pneumatic Manipulator Based on Dynamic Neural Network［C］／／Proceedings of the IEEE International Con-ference on Systems，Wasington：Man and Cybernetics，2003，3：2231．

［11］ 张剑明，田魁岳．基于 Matlab／Simulink的液压伺服系统动态性能仿真研究［J］．工程机械，2007，44（4）：57．ZHANG Jian-ming，TIAN Kui-yue．Simulation Research on Dynamic Performances of a Hydraulic Servo System Based on Matlab／Simulink［J］．Construction Machinery and Equipment，2007，44（4）：57．（in Chinese）

［12］ 韩京清，王学军．非线性PID控制器在机械手控制中的应用［C］／／1993中国控制与决策学术年会论文集，沈阳：东北大学，1993：12．HAN Jing-qing，WANG Xue-jun．The Application of Nonlinear PID Controller in Manipulator Control［C］／／1993Chinese Control and Decision Making Academic Essays， Shengyang： Northeastern University，1993：12．（in Chinese）