多元LDPC码与二元LDPC码的性能分析
陈明阳,高兴龙,王中训,颜飞,殷熔煌
(烟台大学 光 电信息科学技术学院, 山东 烟 台 2 64005)
随着近几年来现代通信技术,软件无线电技术、处理器技术的不断发展,编译码算法被提上了日程,如何找到适应现代通信的好码,是信息理论界不断探索的课题。Gallager提出的LDPC码一直被认为是最接近Shannon限的好码。近年来二元LDPC码得到了极大地发展[1-5],多元LDPC码也在发展当中。多元LDPC码与二元LDPC码有着重要的联系,然而多元LDPC码在性能上相比二元LDPC码更具有优势。本文分别从检验矩阵、Tanner图和BP译码算法方面比较LDPC码的性能,论证了多元LDPC码的确是性能优异的好码,需要我们花大力气去研究。
1 多元LDPC码与二元LDPC码的构建
众所周知,二元LDPC码定义为二元域上的校验矩阵H的零空间,矩阵H的结构具有如下的性质:1)每行有定常重量ρ;2)每列有定常重量r;3)没有两行或两列有多余一个位置上是1,即其对应的Tanner图无四环,从而保证译码的性能。这样的H被称为(γ,ρ)规则的。被H的0空间定义的码称为(γ,ρ)规则LDPC码。其H矩阵具有如图1所示的形式。
多元LDPC码由取自有限域GF(q)元素形成的校验矩阵H定义,本文在验证LDPC码性能将二元矩阵中的非零行用中的非零元素替代。其矩阵具有如图2所示的形式。
2 LDPC码多元矩阵二元矩阵之间的联系

图1 校验矩阵HFig.1 Parity-check matrix H

图2 多元LDPC码校验矩阵HFig.2 Parity-check matrix H for nonbinary LDPC codes
多元LDPC码校验矩阵的元素基于GF(q),而二元LDPC码校验矩阵中的元素基于 GF(2),若 q=2^M,则 GF(q)中任意一个元素都可以用M个二进制位表示,因此可以找到对应多元矩阵的等价二维矩阵[6],其有如图3所示的形式。

图3 多元LDPC码与二元LDPC码校验矩阵关系图Fig.3 Relational graph between nonbinary LDPC codes and binary LDPC codes
对应的Tanner图如图4所示。
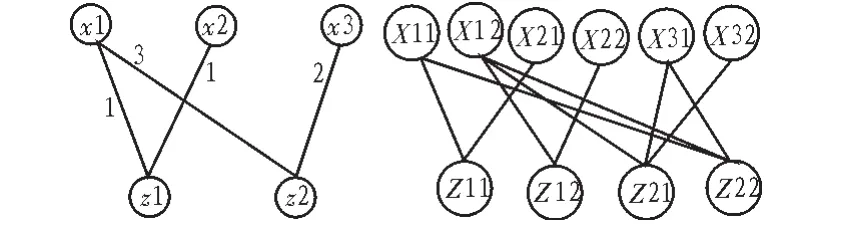
图4 多元LDPC码与二元LDPC码二分图之间的关系Fig.4 Relationship of the bipartite graph between nonbinary LDPC codes and binary LDPC codes
由以上tanner图和LDPC码的校验矩阵可知多元LDPC码的等价二元矩阵存在四环,这就从一定程度上降低了译码性能。
对于给定的译码器,当校验矩阵H的列重量(固定常数)足够大,码长充分大时,LDPC码的性能可以接近shannnon限,即大重量的列有助于译码器的快速纠错,然而若增加列重量会造成相应的双向图中循环数目急剧地增加,从而导致迭代译码的性能下降。而在GF(q=2^P)(q>2)上构造的LDPC码可以很好地解决这个问题。增加它校验矩阵Hq的列重量(即增加与其对应的二进制校验矩阵H2中的列重量),而他们进行译码的双向图是相同的。GF(q)上不会造成结点之间循环路径数目的增加,从而使译码性能得到显著地提高。
3 多元LDPC码与二元LDPC码译码性能的比较
多元LDPC码与二元LDPC码在译码思想上都采用传统的后验概率译码思想,即BP算法。概率信息在校验节点与变量节点之间传递。所不同的是二元LDPC传递概率信息是两个,而多元LDPC码传递的概率信息是q=2^p个。多元LDPC码的传递是将码元信号转化成p个二进制序列在二进制信道进行传递 信道模型如图5所示[7]。
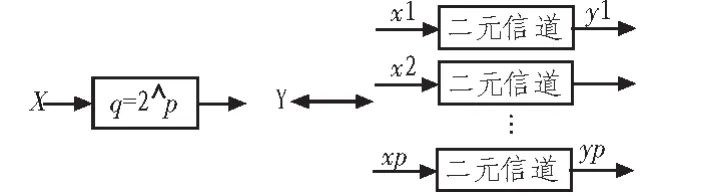
图5 信道模型Fig.5 Information channel model
很明显一个多元码字由p个二进制比特组成,当译码器纠正一个码元时,不管错误出现在其中的一个比特还是多个比特,译码器都将错误码元以为正确的码元。因此当多元码字发生错误时,其中的任何一个比特都有可能发生错误,这样多元LDPC码就具备了更好的抗突发噪声的性能。另外多个比特组成一个码元,由于在编译码环节码字的运算都是采用多进制的运算规则,即一次运算p个比特,因此很大程度上提高了编译码的效率。
具体的性能分析如图6所示。
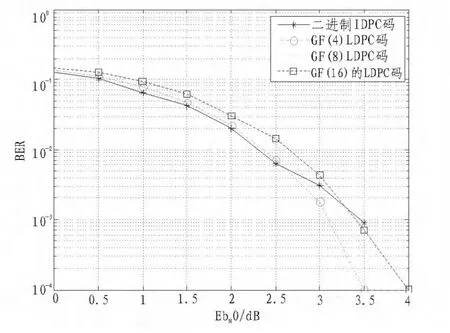
图6 误比特率(BER)与信噪比(Eb_N0)关系图Fig.6 Relational graph on bit error ratio and signal to noise ratio(Eb_N0)
图6是码长为200,码率为0.5时的LDPC码误比特率(BER)与信噪比(Eb_N0)的关系图。由图中可以观察到当码长一定时,随着所取的有限域元素的增多,其性能与与较少元素的矩阵对应的LDPC码基本吻合,某些地方只是略微有些下降。然而事实是矩阵的增大可以降低校验矩阵的构造难度,可以较好的避免短环的出现。因此多元LDPC码相比同等长度码长的二元LDPC码的确有优势。
4 结 论
文章在检验矩阵、Tanner图和BP译码算法方面比较LDPC码的性能,论证了多元LDPC码的确是性能优异的好码,值得研究人员进一步探究。
[1]Gallager R G.Low density parity check codes[D].Cambridge:MIT,1962.
[2]MacKay D J C,Neal R M.Near Shannon limit performance of low density parity check codes[J].Electronics Letters,1996,32(18):1645-1646.
[3]Davey M C.Error-correction using Low-Density Parity-Check code[D].Cambridge:Gonville and Caius College,1999.
[4]Luby M,Mitzenmacher M,Shokrollahi M A.Practical lossresilient codes[C]//Proc.of 29th Annual ACM Symposium on Theory of Computing,1997:150-159.
[5]Luby M,Mitzenmacher M,Shokrollahi M A.Analysis of random processes via and-or tree evaluation[C]//Proc.of 9th Annual ACM-SIAM Symposium on Discrete Algorithms,1998:364-373.
[6]符初生,周亮,文红.LDPC码原理与应用[M].成都:电子科技大学出版社,2006.
[7]张誉.多进制LDPC码译码算法的研究[D].湖南:国防科技大学,2011.

