人工蜂群算法研究综述
曹金保
(陕西师范大学 计算机科学学院,陕西 西安 710062)
传统的优化算法不适宜解决具有高维或者非线性或其他特殊性质的大型问题。群智能算法弥补了传统优化算法的缺陷。在很多困难问题的应用上取得了极其好的效果。群智能属于计算智能的领域[1],目前的研究非常活跃[2]。人工蜂群算法一种是新兴的群智能算法,它具有较强的全局寻优能力,较快的收敛速度和适宜解决多种类型的问题的优点。蜂群算法在2010年的太原群智能会议上作为专题讨论。国外发表的这方面的论文数量增加迅速[3]。目前的研究还处于初期阶段,所获得的研究成果较为分散,算法还有些问题需要解决,对蜂群算法的进一步研究十分必要。通过对其全面系统的总结和评述,能够有效地促进对这一算法的研究和应用。
1 人工蜂群算法的思想
人工蜂群算法(Artificial Bee Colony algorithm,ABC)[4]是建立在蜜蜂自组织模型和群体智能基础上的一种非数值计算优化方法。Seeley[5]关注于蜂群社会行为模式,最早提炼出了蜂群自组织结构模型。Karaboga D[6]于2005年系统提出人工蜂群算法这一群智能随机优化算法。
蜂群算法思想的产生是有其生物学基础的。真实世界中的蜂群由蜂王、工蜂和雄蜂组成[7]。蜂王负责繁殖后代,雄蜂负责与蜂王交配,工蜂负责采集食物、抚育幼虫、照顾蜂王和抵御外敌入侵。人工蜂群算法主要是从工蜂采集食物的过程中抽象出来的。工蜂先从蜂巢出发,随机的在蜂巢周围寻找蜜源。找到蜜源就会采集蜂蜜回到蜂巢将蜂蜜卸下。然后通过跳“8”字摇摆舞向蜂巢的其他工蜂传递信息[8,9]。通过飞行速度、画的“8”字的大小和画“8”字的方向来告知其他蜜蜂蜜源的各种信息。之后就会有很多的蜜蜂跟着跳舞的蜜蜂去采蜜。之后其他的蜜蜂会招引更多的蜜蜂去采蜜,整个蜂群就会高效的采集到花蜜。当某个蜜源被采集完工蜂就会自动的去寻找新的蜜源。
基于工蜂采蜜过程提取出来的人工蜂群算法主要是由3个要素和2种最基本的行为模式组成。三要素是食物源、雇佣蜂和未被雇佣蜂。行为模式是放弃某个蜜源和为某个蜜源招募。
食物源由于距离远近、花蜜量多少等原因,其价值有高有低。一般使用收益度来代表蜜源的所有因素。收益度越高蜜源价值越高,反之则价值越低。解决实际问题建模过程中,蜜源的收益度通常对应于目标函数值得优劣。被雇佣蜂又叫做引领蜂,它们带有蜜源的各种信息,通过“8”字舞与其他蜜蜂以一定的概率来分享这些信息。未被雇佣蜂有两种,一种是侦察蜂,另外一种是跟随蜂。侦察蜂的主要功能是寻找新的蜜源,跟随蜂的主要功能是跟随引领蜂去采蜜。
蜂群实现采蜜过程的流程图如下:
人工蜂群算法满足Millonas的五项群智能原则[10]和Bonabeau等人的4个群自组织的特征[11]。
五项原则:
1)质量原则,蜂群能对蜜源的质量作出判断,可以根据远近、蜜量多少等信息来分辨出蜜源的优劣。
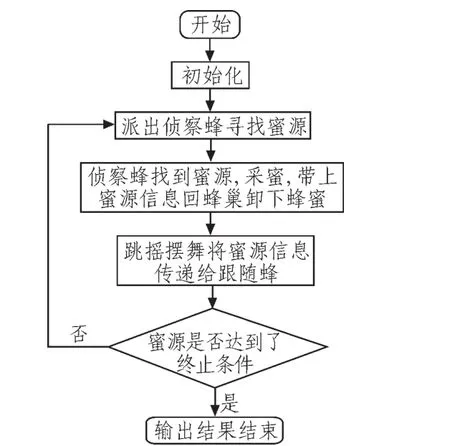
图1 人工蜂群算法流程图Fig.1 Flow chart of ABC
2)邻近原则,蜂群作出时空计算,即蜂群可以搜索蜜源的邻域。
3)多样性原则,蜂群的侦查蜂可以探测新的蜜源,保持蜜源的多样性。
4)适应性原则,蜂群能根据蜜源的变化调整采蜜策略,比如蜂群会放弃某个或者某些蜜源。
5)稳定性原则,蜂群的跟随蜂跟随着找到较好蜜源的引领蜂采蜜,保证了较好蜜源的稳定性,不会轻易被放弃。
自组织的4个特征:
1)正反馈,质量好的蜜源能通过引领蜂吸引机制吸引更多的蜜蜂来采蜜。
2)负反馈平衡,蜜源枯竭或者本蜜源质量排位靠后,蜜蜂就会放弃蜜源作出负反馈。
3)变动性,侦察蜂通过侦查新的蜜源使得蜂群的采蜜过程具有变动性,不会只局限于初始找到的蜜源,蜜源在动态变化中。
4)交互性,蜂群个体之间以及蜂群与环境之间存在着信息的交互,群体可以实现随环境的变化而进化。
由于群智能算法具有并行性与分布式,所以对于当今以数据库形式存在的大量数据非常适合。不仅理论研究有价值,应用研究更有价值。不仅有学术价值更有解决现实问题价值。
2 收敛性证明
对群智能算法的研究,通常关注于能否稳定、快速、高效地获得最优解,对算法的理论分析较少。算法的收敛性是算法最重要的性质之一。蜂群算法由于其随机性使得其收敛性的严密证明具有一定的难度。本章将对蜂群算法收敛性的证明[12]进行介绍。
2.1 算法的数学描述
人工蜂群算法定义了3种蜜蜂:侦察蜂、引领蜂和跟随蜂。这3种蜜蜂构成了蜜蜂角色集合R。算法中的蜜蜂由3方面描述:第一是蜜蜂当前所在的位置x;第二是蜜蜂搜索过程中的最优位置g;第三是蜜蜂的角色r。 蜜蜂B=(x,g,r)。 所有的蜜蜂构成了蜂群空间B可行解的集合是S。适应度函数是 蜜蜂所有的可能的状态的集合构成了蜜蜂的状态空间H。蜂群经过的所有位置中的最优位置就是群体的最优位置gbest。 状态集合状态总量用 φ(H,B)来表示。 若H1,H2∈H,∀B∈B 使得 φ(H1,B)=φ(H2,B),则称H1和H2等价,记作H1≌H2。蜂群的状态是我们所关注的重点,而哪个状态先发生那个状态后发生并没有多大的影响。引入等价关系可以使得证明过程得以进行。
2.2 算法收敛性证明所需的数学知识
定义1:若有随机过程{Xn,n∈T},其中T是离散的随机序列,离散的状态集I是由Xn所有可能取值的全体组成的状态空间。假如任意的T和任意的I,条件概率满足
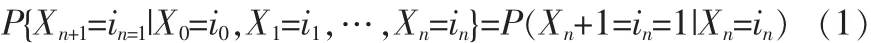
则称这个随机过程为离散时间Markov链。式1是Markov链无后效性(也叫Markov性)的表达式。
定义Markov链的转移概率为

其中i,j∈I。
定义 2:如果任意的i,j∈I,Markov 链{Xn,n∈T}的转移概率Pi,j(n)都和n无关,就称 Markov 链是齐次的,并记Pi,j(n)为Pi,j。
定义 3:称pi=P{X0}=i(i∈I)和Pi(n)=P{Xn=i}(i∈I)为Markov链的初始概率和绝对概率
定义 4:称{pi,i∈I}和{pi(n)=P{Xn,i∈I}}是初始分布和绝对分布,也可以记为{pi}和{pi(n)}。
定义5:n步转移概率为=P{Xm+n=j|Xm=i},n步转移矩阵为p(n)=(),其中P
2.3 算法的收敛性证明
蜜蜂从状态经过一步转移到B2状态这一过程如下式所示:

蜂群的位置转移概率用下式表示:

搜索过程中的最佳位置g的转移概率用下式表示:

算子Tp[f]定义如下式:
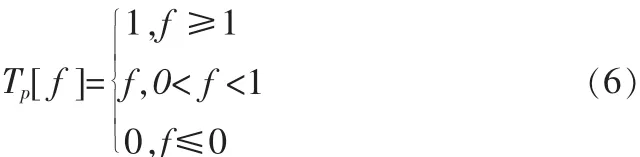
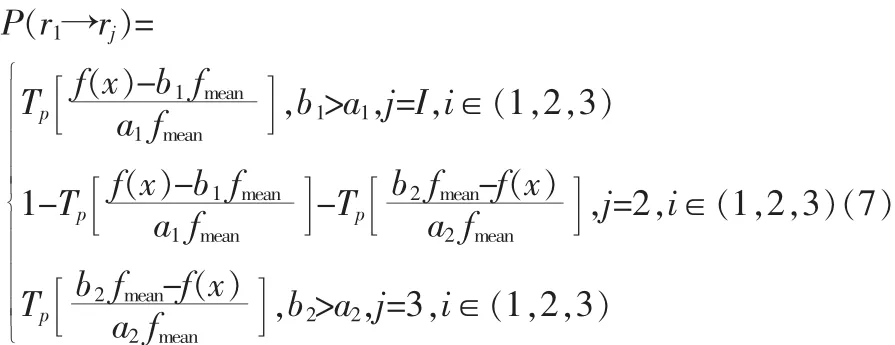
角色转换的概率定义如下式:蜜蜂的状态转移概率由下式表示:

蜂群从状态Hi一步转移到状态Hj的转移概率如下式所示:
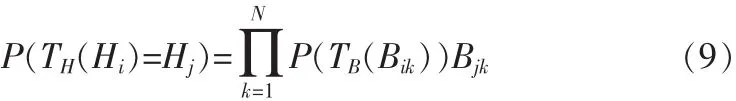
只需证得蜂群状态序列是有限齐次Markov链,就可以证明蜂群算法是收敛的。
证明:因为蜂群算法的搜索空间是有限的,任何一个蜂群状态下的三要素也都是有限的,所以,蜂群的状态空间就是有限的。
任意一个H(k-1),H(k)∈S蜂群的状态序列{H(k),k≥0}中,对应的转移概率P(TH(H(k-1)=Hk))都是由蜜蜂的转移概率P(TB(Bi)(k-1))=Bi(k)所决定。 而蜜蜂的转移概率又是由位置转移概率、最优位置转移概率和角色转移概率三者决定。这三者又只与x,g,r和全局最优解gbest相关。gbest是所有的g 中的最优值。P(g(k-1)→g(k))只与P(x(k-1)→x(k))和P(g(k-1))相关,所以说P(g(k-1)→g(k))也只与x,g,r和全局最优解gbest相关。P(TH(H(k-1)=Hk))只与蜜蜂状态相关,也就是{H(k),k≥0}具有Markov性。蜂群的状态空间是离散又有限的,所以是有限 Markov 链。 因为P(x(k-1)→x(k))、P(g(k-1)→g(k))和P(r(k-1)→r(k))都与时间无关,所以P(TB(B(k-1))=B(k))也与时间无关,最终P(TH(H(k-1)=Hk))也与时间无关,是齐次的。得证{H(k),k≥0}是有限齐次Markov链。
通过证明蜂群的状态序列是有限齐次Markov链,证明了蜂群算法的收敛性。
3 人工蜂群算法的研究与应用的现状
国内外研究主要从两方面进行,一是算法的改进,另外一方面是算法的应用。
算法改进的已有研究主要有:何宗耀等将蜂群算法与蚁群算法融合,设计了一种参数自适应机制。王辉通过调整信息共享程度和在算法后期减弱食物源对蜂群的影响两方面对蜂群算法进行了改进。毕晓君等改变轮盘赌选择模型对蜂群算法进行了改进。韦新丹将模拟退火算法引入改进了蜂群算法跟随蜂的邻域搜索过程。王志刚将粒子群与蜂群算法进行了融合。向万里提出一种轮盘赌反向选择机制来保持蜂群个体的多样性。李卫华等将蜂群算法与BP神经网络算法融合。毕晓君等提出了一种加速收敛的人工蜂群算法。王辉提出了一种带有共享因子的人工蜂群算法。暴励等提出了一种双种群差分蜂群算法。林小军等提出了一种云变异人工蜂群算法。罗钧等用遗传算法改进了蜂群算法。
算法应用的研究成果主要有:Karaboga D等用ABC解决约束优化问题、聚类分析和训练神经网络。赵良辉等用蜂群算法解决了集聚约束调度问题。Pulikanti等把ABC和贪婪算法、局域搜索算法结合来求解二次方程渐缩的问题。李林菲等应用ABC算法快速求解逻辑推理问题。Kang等将ABC与单纯形法结合来解决逆分析问题。拓守恒用 算法解决高维约束优化问题。樊小毛等用ABC解决经典的0-1背包问题。赵小强等用ABC算法解决模糊聚类问题。Rao等人用ABC算法来优化多工序制粉操作过程的参数。胡中华等用ABC算法来求解TSP和JSP问题。梁建慧等将ABC算法应用在了图像分割问题中。肖永豪等将ABC算法应用在图像边缘检测问题中。Hsieh等人将ABC算法应用到股票价格预测问题中。黎竹娟将ABC算法应用到移动机器人路径规划问题中。Karaboga将ABC算法应用到数字无限脉冲反应过滤器设计问题中。姚婧等将ABC算法用于解决云计算负载平衡问题。Rebreyend等人把ABC与贪婪算法结合来优化多处理机调度问题。Sundar等将ABC算法应用于求解二次的最小生成树问题。王慧颖等改进了蜂群算法并且应用在了函数优化问题中。Banharnsakun等用最优选择法改进ABC算法并应用于图像配准问题。任新新等将ABC算法应用于配电网无功优化问题上。Bernardino等用ABC算法解决加权环网负荷的问题。刘敏等将ABC算法应用于无人机航路规划与平滑问题当中。Ho等将ABC算法应用于求逆电磁问题。周文越等应用ABC算法解决电力系统保护与控制问题。Omkar等用ABC算法解决多目标复合件设计问题。于君等用ABC算法创造出了一种制作群体动画的方法。Hetmaniok等用ABC算法解决了逆热传导问题。张姣玲用ABC算法解决了非线性方程及方程组的求解问题。吕聪颖等用模糊人工蜂群算法解决了加工中心组成问题。算法应用如此之广泛,可见其应用前景非常广阔。
4 人工蜂群算法与其他算法的对比分析
4.1 人工蜂群算法与其他群智能算法共同点的分析
人工蜂群算法与其他群智能算法有很多的共同点:
1)都是由多个简单的智能体组成的。智能体与智能体、智能体与环境之间有交互作用。
2)都是自组织的。他们没有一个中央控制器,完全靠每个个体的简单行为模式出现自组织特性。
3)都是不确定的概率型算法。算法的过程以及最终求得的结果,往往是随机的,只要其保持收敛性,算法就有可能有较大的机会求得全局最优解。
4)都具有广泛的适用性。算法可以广泛应用于解决各种优化问题。对问题的数学特征和结构特征要求不严格。很多时候一个适应度函数就可以解决问题。
5)都是收敛的有效的算法。
6)都具有并行性。这些算法与算法可以并行,而且算法本身的计算过程中存在着并行性。
4.2 人工蜂群算法与其他重要群智能算法优缺点对比分析
人工蜂群算法与其他重要群智能算法优缺点对比分析结果如下面的表1所示。
5 结束语
蜂群算法的应用与研究取得了很多的进展,也证明了蜂群算法[13]具有良好的性能。未来的研究仍然有很多的突破口与切入点。

表1 4种群智能算法优缺点对比分析表Tab.1 Advantages and disadvantages comparative analysis table for several swarm intelligence algorithm
1)理论方面。由于蜂群算法是一种概率搜索算法,从严格的数学意义上证明蜂群算法的正确性与可靠性相当困难。对其收敛性的证明也可以从不同的角度进行,也不仅仅是Markov理论这一种。参数选择、种群分配以及收敛速度等问题,由于其经验性和直觉性,缺乏严格的数学论证。
2)模型方面。蜂群不仅仅只有抽象出来的这几种行为模式而已,可以从这种思路提出更好的蜂群算法。也可以借鉴其他算法的模型,进行算法的融合操作。
3)应用领域方面。现有的研究大部分是止步于仿真阶段,都对现实情况进行了简化,所以可以更加深入的向实际问题应用靠近。
4)硬件实现方面。可以将蜂群算法用硬件实现,但是产品的鲁棒性、可靠性等问题需要深入探索。也可以研制蜂群算法的仿生平台,订立产品的技术标准。
[1]Krol D,Drozdzowski M.Use of MaSE methodology for designing a swarm-based multi-agent system[J].Journal of Intelligent and Fuzzy Systems,2010,21(3):221-231.
[2]Sabat S L,Udgata S K,Abraham A.Artificial bee colony algorithm for small signal model parameter extraction of MESFET[J].Engineering Applications of Artificial Intelligence,2010,23(5):689-694.
[3]Karaboga D.A survey algorithms simulating bee swarm intelligence[J].Artificial Intelligence Review,2009,31(1-4):61-85.
[4]Karaboga D,Akay B.A comparative study of Artificial Bee Colony algorithm[J].Applied Mathematics and Computation,2009,214:108-132.
[5]Seeley T D.The wisdom of the hive:the social physiol-ogy of honey bee colonies[M].Boston,Massachusetts,USA:Harvard University Press,1995.
[6]Karaboga D.An idea based on honey bee swarm for numerical optimization[R].Technical Report-TR06.Erciyes University,2005.
[7]Horng M H,Jiang T W.Image vector quantization algorithm via honey bee mating optimization[J].Expert Systems with applications,2011,38(3):1382-1392.
[8]Camazine S,Deneubourg J L,Franks N R,et al.Selforganization in biological systems[M].Princeton:Princeton University Pres,2003.
[9]Dereli T,Das G S.A hybrid bee (s) algorithm for solving container loading problems[J].Applied Soft Computing,2011,11(2):2854-2862.
[10]MillnasM M.Swarms,phase transitions,and collective intelligence[C]//Proc of Artificial LifeⅢConference.New York,Addison-Wesley Publishing Company,1994:417-445.
[11]Bonabeau E,Dorigo M,Theraulaz G.Swarm intelligence:from natural to artificial systems[M].New York:Oxford University Press,1999.
[12]肖永豪.蜂群算法及在图像处理中的应用研究[D].广州:华南理工大学,2011.
[13]黄孝伦.蜂群算法在智能交通中的应用研究[J].现代电子技术,2010(14):134-135,139.
HUANG Xiao-lun.Applied research of bee colony algorithm in intelligent transportation System[J].Modern Electronics Technique,2010(14):134-135,139.

