混合励磁永磁电机齿谐波绕组特性计算与分析

夏永洪， 黄劭刚

(南昌大学信息工程学院，江西南昌 330031)

0 引言

通过在永磁电机内部增加电励磁的方式形成的混合励磁永磁电机，克服了永磁电机气隙磁场调节困难的缺点［1－2］。经过国内外学者多年的研究，已经取得了一定的研究成果，提出了近30种混合励磁永磁电机结构。根据永磁磁动势和电励磁磁动势在磁路上的串、并联的关系，可将混合励磁永磁电机分为串联混合励磁永磁电机［3－4］和并联混合励磁永磁电机［5－6］两大类。

对于串联混合励磁永磁电机，由于永磁体的磁导率接近空气，为了调节电机气隙磁场，需要输入较大的励磁电流，导致励磁损耗增加，从而降低永磁电机的效率。对于并联结构的混合励磁永磁电机，通常所需的电励磁磁动势较小，因此，具有较高的效率。然而，有些并联结构的混合励磁永磁电机却失去永磁电机无刷无励磁机等优点，即在没有交流励磁机的情况下仍需要电刷和滑环等机械装置［5－6］。

巧妙地将齿谐波励磁与永磁励磁相结合形成的齿谐波励磁的混合励磁永磁同步发电机为解决现有一些混合励磁永磁电机无刷化问题提供了一个有效途径［7－8］。该电机利用气隙中的齿谐波磁场在转子齿谐波绕组中感应的齿谐波电动势，经二极管整流后提供给发电机的励磁绕组进行励磁，励磁绕组产生的磁动势用于调节电机的气隙磁场［7］。

准确计算齿谐波绕组特性是分析和设计该类电机的前提。电磁场有限元法已经成为计算电机性能的一种常用工具。通过求解一次电机电磁场得到气隙磁密波形，利用傅里叶级数对其分解得到各阶齿谐波磁密大小，进而计算转子齿谐波绕组感应电动势有效值。然而，当转子相对定子处于不同位置时计算得到的气隙磁密波形并不相同［9］;并且磁动势作用在定子齿谐波磁导上产生的某些齿谐波磁密次数与磁动势作用在平均气隙磁导上产生的谐波磁密次数相同，计算时难以将两者解耦。因此，采用该方法计算齿谐波绕组的空载和负载特性会产生一定的误差，并且不能准确得到齿谐波绕组电动势波形。

为此，本文首先分析转子齿谐波电动势的产生机理;根据转子齿谐波电动势的特点，分析转子齿谐波绕组电动势的变化周期，然后基于电磁场有限元法，求解一周期内不同时刻、定转子不同位置下的电磁场，根据电磁场计算结果得到转子齿谐波绕组磁链波形，进而准确计算转子齿谐波绕组电动势波形和有效值。通过改变励磁电流和电枢电流，得到转子齿谐波绕组电压随励磁电流和电枢电流的变化曲线，分析其变化原因，并用实验结果加以验证。

1 转子齿谐波电动势产生机理

同步发电机运行时，转子以同步速旋转，因此，转子开槽引起的齿谐波磁场相对转子静止，不会在转子侧感应齿谐波电动势，即转子齿谐波电动势主要是由定子开槽产生的［7］。

励磁磁动势作用在定子齿谐波磁导上产生的齿谐波磁场为

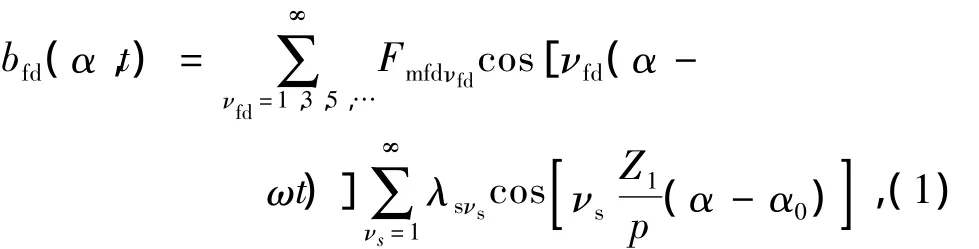
式中:α为定子坐标系电角度;t为时间;Fmfdνfd为νfd次谐波磁动势幅值，νfd为奇数;ω为电机旋转电角速度;λsνs为定子各阶齿谐波磁导幅值(文中的磁导均指单位面积的磁导);νs为定子齿谐波磁导阶数;Z1电机定子槽数;p为电机基波极对数;α0为定子齿中心线领先定子坐标系轴线电角度。

当齿谐波励磁的混合励磁永磁同步发电机负载运行时，则势气隙中的齿谐波磁场由励磁磁动势和电枢磁动势共同产生。电枢磁动势中除了基波磁动势外，还有谐波磁动势。由于电枢绕组的短距和分布，电枢谐波磁动势含量较少，可以忽略其作用在定子齿谐波磁导上产生的齿谐波磁场对转子齿谐波电动势的影响。

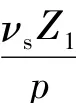
2 转子齿谐波绕组电动势波形计算

2.1 齿谐波绕组电动势的变化周期

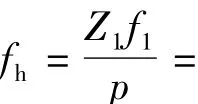
当齿谐波励磁的混合励磁永磁同步发电机负载运行时，基波电枢磁动势作用在定子齿谐波磁导上产生的齿谐波磁密在转子齿谐波绕组中感应的齿谐波电动势频率与发电机空载运行时相同，即发电机负载运行时转子齿谐波绕组电动势变化周期与空载时相同，仍为一个定子齿距角。

2.2 绕组电动势波形计算

将一个定子齿距分成n等份，利用有限元法计算一个定子齿距内定、转子n个不同位置下的电磁场，获取转子槽口在n个不同位置下的矢量磁位。根据矢量磁位以及电机铁心长，计算转子各个齿在n个不同位置的磁通，即转子各个齿在一周期内的磁通可用向量形式表示为

式中:下标 j为转子齿序号，j=1，2，…，Z2，Z2为电机转子槽数。

电机所有转子齿磁通可用矩阵形式表示为

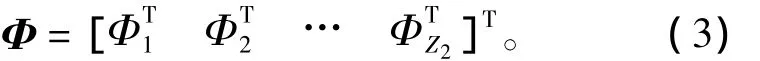
根据构成转子齿谐波绕组的每个线圈匝数及线圈绕向，得到转子齿谐波绕组匝数向量N［10］。由式(3)和匝数向量N计算转子齿谐波绕组磁链，可得

式中:ψg为转子齿谐波绕组在一个周期内的磁链向量。

根据式(4)计算转子齿谐波绕组感应电动势波形，可得

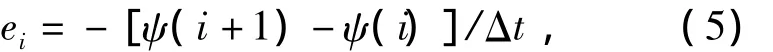
式中:i表示转子齿谐波绕组磁链第i个元素;Δt为转子旋转一步的时间。

3 计算结果和实验结果比较

为了验证齿谐波绕组电动势波形计算的准确性，本文对一台齿谐波励磁的混合励磁永磁同步发电机的齿谐波绕组特性进行了理论计算和实验，图1是电机的截面图和原理图。

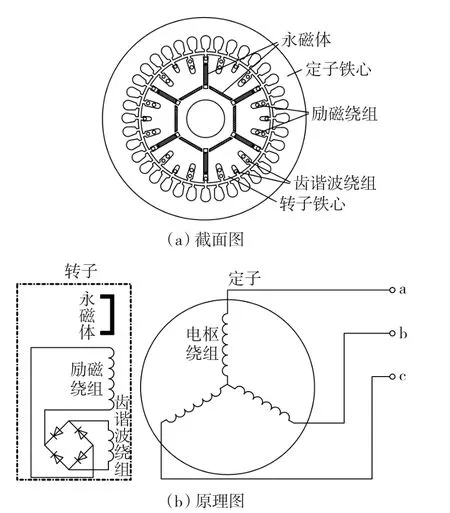
图1 齿谐波励磁的混合励磁永磁同步发电机Fig．1 The hybrid excitation permanent magnet synchronous generator utilizing tooth harmonic for excitation

电机参数:额定功率为3.0 kW，额定电压为220 V，额定电流为8.75 A，额定频率为50 Hz，极对数为3，相数为3，定子槽数为45，转子槽数为60，定子电枢绕组为Y接，并联支路数为1，每相串联匝数为120匝，转子齿谐波绕组串联匝数为186匝，励磁绕组串联匝数为330匝，定子直槽，定子外直径为260 mm，转子外直径为 178.2 mm，气隙长度为0.9 mm，铁心长度为100 mm，定子槽口宽为5.2 mm，转子槽口宽为3.6 mm。为了方便实验时能够直接测量转子齿谐波绕组和励磁绕组的电压以及电流，在样机的轴端安装了电刷和滑环。

根据齿谐波绕组感应电动势波形计算方法，得到了发电机空载和负载运行时齿谐波绕组感应电动势的波形和有效值，分别如图2、图3和表1所示。

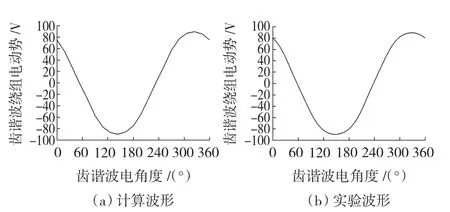
图2 当电机空载运行时齿谐波绕组电动势波形Fig．2 The EMF waveform of the tooth harmonic windings under no-load operation

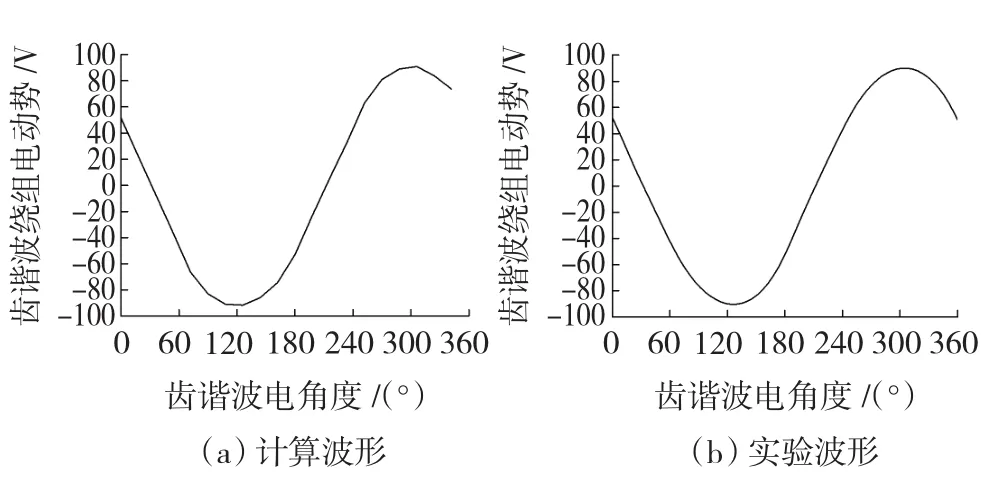
图3 当电枢电流Ia=6.71 A、功率因数cosφ=0.9(滞后)时齿谐波绕组电动势波形Fig．3 The EMF waveform of the tooth harmonic windings for Ia=6.71 A and cosφ=0.9(lagging)

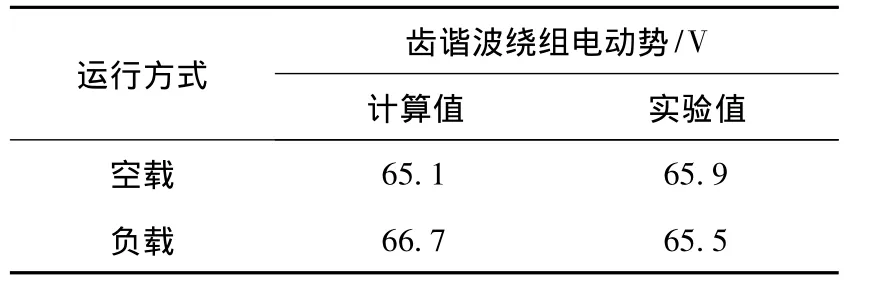
表1 与图2和图3对应的齿谐波绕组电动势有效值Table 1 The effective value of the EMF of the tooth harmonic windings for Fig．2 and Fig．3

由图2、图3以及表1的对比可知，计算结果和实验结果基本吻合，验证了计算方法的准确性。

通过改变励磁电流和电枢电流的大小，得到了齿谐波绕组电压随励磁电流和电枢电流的变化曲线，如图4和图5所示。

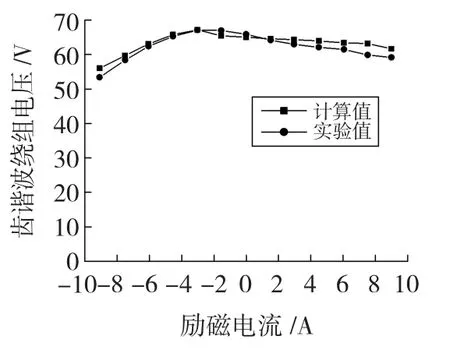
图4 当电枢电流为0时齿谐波绕组电压随励磁电流的变化Fig．4 Changes of the tooth harmonic winding voltage with field current when armature current is zero

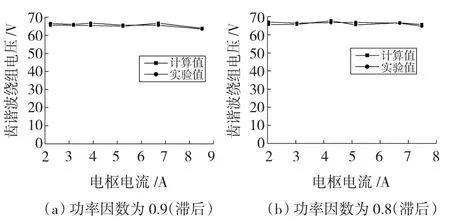
图5 当励磁电流为0时齿谐波绕组电压随电枢电流的变化Fig．5 Changes of the tooth harmonic winding voltage with armature current when field current is zero

由图4和图5可知，当发电机空载运行时，随着励磁电流正向逐渐增大，齿谐波绕组电动势逐渐减小;而当励磁电流反向逐渐增大时，齿谐波绕组感应电动势先是增大，然后逐渐减小。当发电机负载运行时，无论功率因数为0.9(滞后)还是0.8(滞后)，随着电枢电流的增大，齿谐波绕组电动势基本不变。与同步发电机电枢绕组空载特性和外特性的变化趋势不同，下面将详细分析产生这一现象的原因。

4 转子齿谐波绕组特性分析

为了提高材料的利用率，仅当永磁体单独作用时，齿谐波励磁的混合励磁永磁同步发电机齿部和轭部已经处于饱和状态。随着励磁电流的正向增大，磁路将更加饱和，铁磁材料的磁阻也增大。为了分析方便，现将铁磁材料的磁阻归算到气隙中，通过适当放大气隙的长度进行考虑。则考虑铁心磁路饱和后的电机等效气隙长度为

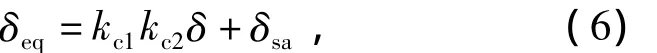
式中:kc1为考虑定子开槽的卡氏系数;kc2为考虑转子开槽的卡氏系数;δ为电机气隙长度;δsa为考虑铁心磁路饱和的等效气隙长度。

定子一阶齿谐波磁导［11］为

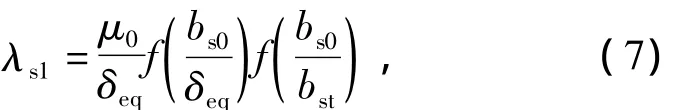
式中:μ0为空气磁导率;bs0为定子槽口宽度;bst为定子齿距。

由式(7)可知，当气隙长度增加时，齿谐波磁导减小。因此，随着励磁电流正向增大，电励磁磁动势也增大，使得永磁磁动势和电励磁磁动势产生的合成励磁磁动势增大，磁路逐渐饱和，等效气隙逐渐增大，齿谐波磁导逐渐减小，齿谐波磁密也逐渐减小，从而导致齿谐波绕组感应电动势随着励磁电流的增加而下降。当励磁电流反向增大时，永磁磁动势和电励磁磁动势产生的合成励磁磁动势减小，磁路饱和程度降低，齿谐波磁导增大，齿谐波磁密在一定的励磁电流范围内有可能增大，使得齿谐波绕组电动势也增大;当励磁电流进一步反向增大时，磁路处于不饱和状态，齿谐波磁导基本不变，因此，齿谐波磁密减小，齿谐波绕组电动势也减小，如图4所示。

当电机负载运行时，由于电枢反应的去磁作用，合成基波气隙磁动势比基波励磁磁动势小，磁路饱和程度降低，齿谐波磁导增大，齿谐波磁密在一定的电枢电流范围内有可能保持不变，相应地，齿谐波绕组电动势也基本不变，如图5所示。

5 结语

针对混合励磁永磁同步发电机齿谐波绕组特性进行了计算与分析，基于电磁场有限元法，提出了一种准确计算齿谐波绕组电动势波形的方法，应用该方法计算了发电机空载和负载运行时的齿谐波绕组特性。齿谐波绕组特性与电枢绕组特性变化趋势不同，其受磁路饱和影响较大。计算结果和实验结果基本吻合，验证了计算方法的准确性与理论分析的正确性。

［1］WANG Shanming，XIA Yonghong，WANG Xiangheng，et al．State of the art of hybrid excitation permanent magnet synchronous machines［C］//Proceedings of the 13th International Conference on Electrical Machines and Systems，October 10－13，2010，Incheon，Korea．2010:1004 －1009．

［2］赵朝会，秦海鸿，严仰光．混合励磁同步电机发展现状及应用前景［J］．电机与控制学报，2006，10(2):113－117．

ZHAO Chaohui，QIN Haihong，YAN Yangguang．Present status and application perspective of hybrid excitation synchronous machine［J］．Electric Machines and Control，2006，10(2):113－117．

［3］FODOREAN D，DJERDIR A，VIOREL I A，et al．A double excited synchronous machine for direct drive application-design and prototype tests［J］．IEEE Transactions on Energy Conversion，2007，22(3):656－665．

［4］赵朝会．串联磁路混合励磁爪极发电机的结构设计和特性［J］．电工技术学报，2009，24(5):1－6，12．

ZHAO Chaohui．Structure designing and characteristic study of hecpg which magnetic circuit series connection［J］．Transactions of China Electrotechnical Society，2009，24(5):1 －6，12．

［5］AMARA Y，VID O L，GABSI M，et al．Hybrid excitation synchronous machines:energy-efficient solution for vehicles propulsion［J］．IEEE Transactions on Vehicular Technology，2009，58(5):2137－2149．

［6］夏永洪，黄劭刚．混合磁极式的混合励磁永磁同步发电机仿真［J］．电机与控制学报，2012，16(8):23－28．

XIA Yonghong，HUANG Shaogang．Simulation of hybrid excitation permanent magnet synchronous generator with hybrid poles［J］．E-lectric Machines and Control，2012，16(8):23 －28．

［7］夏永洪，王善铭，黄劭刚，等．齿谐波励磁的混合励磁永磁同步发电机［J］．清华大学学报:自然科学版，2011，51(11):1557－1561．

XIA Yonghong，WANG Shanming，HUANG Shaogang，et al．Hybrid excitation permanent magnet synchronous generator utilizing tooth harmonic for excitation［J］．Journal of Tsinghua University:Science and Technology，2011，51(11):1557 －1561．

［8］夏永洪，王善铭，邱阿瑞，等．新型混合励磁永磁同步电机齿谐波电动势的协调控制［J］．电工技术学报，2012，27(3):56－61．

XIA Yonghong，WANG Shanming，QIU Arui，et al．Coordinated control of tooth harmonic emf of novel hybrid excitation permanent magnet synchronous machine［J］．Transactions of China Electrotechnical Society，2012，27(3):56－61．

［9］夏永洪．谐波励磁同步发电机谐波绕组电压分析［D］．南昌:南昌大学信息工程学院，2005:27－30．

［10］夏永洪，王善铭，黄劭刚，等．齿谐波绕组感应电动势波形快速计算［J］．电机与控制学报，2011，15(9):1 －5．

XIA Yonghong，WANG Shanming，HUANG Shaogang，et al．Fast calculation of the induced EMF waveform of the tooth harmonic windings［J］．Electric Machines and Control，2011，15(9):1－5．

［11］HELLER B，HAMATA V．异步电机中谐波磁场的作用［M］．章名涛，俞鑫昌，译．北京:机械工业出版社，1980:48－61．