自起动永磁电机复合材料转子导条的优化
卢伟甫, 赵海森, 刘明基, 罗应立
(华北电力大学电气与电子工程学院,北京 102206)
0 引言
普通自起动永磁同步电机(line-start permanent magnet synchronous motor,LSPMSM)的起动电流比同规格的异步电动机还要大[1-3],过大的起动电流可能导致永磁体的不可逆退磁。而带有复合材料起动导条的永磁电机[4-5],与普通自起动永磁同步电机相比,改进之处在于转子导条两侧增加了一部分导磁导电的合金,改变了原来导条只由导电材料构成的特性。在起动过程中,转子导条的合金部分起主要作用,其材料的集肤效应使起动过程中转子的等效电阻增大,从而得到较大的起动转矩及较小的起动电流,使起动过程中退磁磁场变小;另一方面铜铁合金材料的存在相当于为定转子电流合成磁场提供了一个漏磁路,也使得穿过永磁体的退磁磁场进一步减小,因此带有复合材料转子导条的永磁电机具有较高的抗退磁能力。
复合材料转子导条尺寸和合金本身的电磁特性将影响电机的起动和运行性能。本文利用时步有限元方法分析了复合材料导条结构尺寸和合金材料电磁特性对永磁电机性能的影响。为了使永磁电机得到较好的起动性能和较高的抗退磁能力,鉴于分析结果,以导条结构宽度、合金材料的磁导率和电导率为设计变量,首先利用正交试验表进行正交试验设计,然后利用正交试验结果拟合出各项性能指标的二次响应面回归方程,并以抗退磁能力为优化目标,以自起动永磁电机的堵转电流倍数、堵转转矩倍数的要求作为约束条件,构造增广目标函数,并将其作为遗传算法的适应度函数进行优化,最终利用遗传算法搜索出最优目标以及对应的转子导条尺寸和材料电磁特性。优化后的复合材料转子导条从根本上提高了永磁电机的抗退磁能力,并得到了比普通永磁电机大的堵转转矩和小的堵转电流,实现了优化目标。
1 复合材料导条对电机性能的影响
1.1 带有复合材料导条永磁电机的性能分析
自起动永磁电机转子中的永磁体多采用内嵌式结构,永磁体的外面是鼠笼起动导条,起动时依靠起动导条中的感应电流产生力矩,实现永磁电机的异步起动,起动完成后由永磁磁场与定子磁场共同产生的驱动转矩将转子牵入同步运行状态。永磁电机在起动过程中的定子电流主要有两部分构成,一是由于外施电压所产生鼠笼异步电机效应的定子电流;二是永磁体磁场作用于定子绕组且定子绕组等效短路所产生的变频永磁发电机短路电流。这两方面的因素使得自起动永磁电机的起动电流要比同规格的异步电机大的多,从而使得永磁体面临退磁危险。而带有复合材料导条的自起动永磁电机在普通转子导条两侧增加了具有一定磁导率和电导率的合金材料,如铜铁合金,从而改变单一的导电材料,使得计算出来的透入深度减小,起动过程中的等效电阻得以增大,使堵转电流减小,同时导条中既导磁又导电的合金部分也为电枢反应退磁磁场提供了一定的漏磁路,避免了过多电枢退磁磁场穿过永磁体引起的永磁体退磁。
通过优化复合材料导条的结构尺寸和材料导磁导电特性,在保证永磁电机基本性能的基础上,可以得到更优的起动性能和抗退磁能力。其中,电机的起动性能参数包括堵转转矩和堵转电流,电机的抗退磁能力由空载起动过程中永磁体的最低工作点磁密来表征[1,6]。本文采用能够计及饱和、集肤效应等多种非线性因素影响的时步有限元法计算和分析电机的性能参数。永磁电机的电磁场瞬态边值问题,可表示为
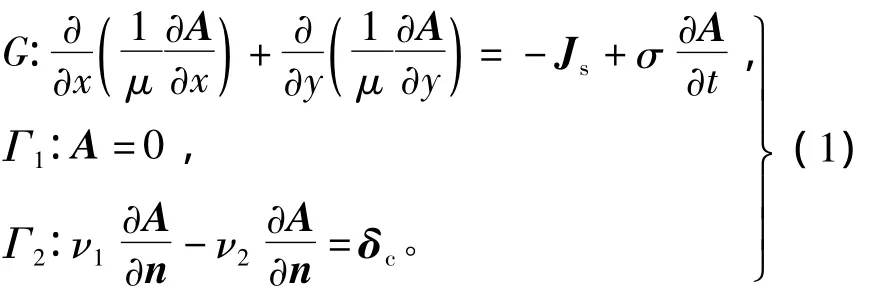
式中:A为矢量磁位,Js为传导电流密度;μ为磁导率,σ为电导率;v1,v2为不同介质的磁阻率;δc为永磁体等效面电流密度,δc=Hc×n,其中Hc为永磁体矫顽力,n为永磁体边界外法向单位矢量;G为求解区域;?Γ1为定子铁心外圆边界;?Γ2为永磁体和其他媒介的交界。
将式(1)的电磁场边值问题离散并联立电机的定、转子电路方程、运动方程得到永磁电机的场-路-运动耦合方程。在特定条件下求解方程,便可得到电机的堵转转矩、堵转电流以及永磁体单元磁密等性能参数[7]。
1.2 复合材料导条尺寸对性能的影响
复合材料转子导条结构如图1所示,中间部分为只导电不导磁的黄铜材料,两侧为既导磁又导电的铜铁合金材料,调整转子导条各部分尺寸以及合金材料部分的电磁特性可以改变转子电阻及漏抗,从而影响电机性能。
如图1所示复合材料导条可调整的尺寸变量有中间黄铜宽度br1,导条上端总宽度br4以及导条高度hr2,由于永磁电机转子槽深限制,hr2变化不大,因此主要改变br1,br4。根据电机结构,转子槽型宽度br4过小会导致性能过低、转子空间利用率不高等问题,过大又容易导致相邻转子槽间的铁磁材料机械强度不够,因此根据本文所分析的样机结构,设定br4=12.03 mm,hr2=17.42 mm。导条尺寸只须调整中间黄铜宽度br1,如图2所示。

图1 复合材料导条结构图Fig.1 Composite material bar structure

图2 不同br1复合材料导条示意图Fig.2 Composite material bars with different br1
本文利用时步有限元法分析比较了不同br1下复合材料转子导条永磁电机的性能参数,包括堵转转矩倍数Tst,堵转电流倍数Ist,空载起动过程中永磁体最低工作点磁密Bmin以及空载感应电动势E0,如图3(a)~图3(d)所示。

图3 不同br1下电机性能参数比较Fig.3 Parameter comparisons of models with different br1
由图3可见,增大br1,可以使得堵转转矩和空载感应电动势增大,但也使得堵转电流随之增大,永磁体最低工作点磁密减小。因此需根据电机的性能要求综合考虑,选择合适的导条尺寸br1。
1.3 复合材料导条合金材料电磁特性对性能的影响
如图1所示,复合材料导条共有两种材料属性,其中导条中间部分采用导电材料如铸铝、紫铜或黄铜等,本文选用黄铜,其磁导率默认为空气磁导率;两侧采用铜铁合金材料,其电磁特性可以通过改变导电、导磁金属的比例来调节。设定铜铁合金材料的电导率可取值的范围为:σr=0.25σr0~ σr0,磁导率可取值的范围为:μr=30μ0~ 120μ0,其中 σr0和 μ0分别为合金电导率和磁导率的基值,取值为σr0=5.87×106S/m,μ0=4π ×10-7H/m。图 4(a)~ 图4(c)给出了堵转转矩倍数Tst,堵转电流倍数Ist和空载起动过程中永磁体最低工作点磁密Bmin各自与合金电导率倍数σr/σr0和磁导率倍数μr/μ0的关系曲面图。
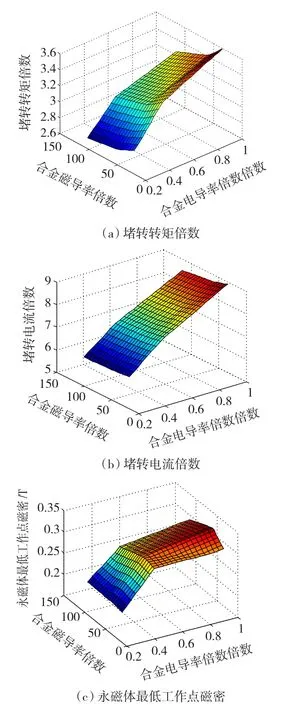
图4 不同合金电磁特性下电机性能比较Fig.4 Performance comparisons of models with alloy of different electromagnetic characteristics
由图4可见,随着合金材料电导率的增加,堵转转矩和堵转电流同时增大;随着合金材料磁导率的增加,堵转转矩和堵转电流同时减小。永磁体最低工作点磁密随合金电导率和磁导率变化的规律不明显。
综上所述,可见复合材料导条参数直接影响电机起动性能和抗退磁能力。因此为获得较大的堵转转矩和较小的堵转电流以及较高的抗退磁能力,对复合材料导条尺寸变量br1和合金材料电磁特性变量σr/σr0、μr/μ0进行优化设计。
2 正交试验设计
正交试验设计是一种解决多因素、多水平试验问题的有效方法,它利用正交表Ln(pf)安排少数次试验,就能找到最好或者较好的试验条件,因此它被广泛地用于寻优[8-10]。Ln(pf)表示一个具有f个因素和p个水平的正交表,其中L表示拉丁方,n表示水平组合数。对f因素、p水平的试验问题,若进行全面组合试验,则要做pf组试验,但是当p和f很大时,不可能做pf组试验,而应用正交表Ln(pf)来安排正交试验,只需要选择n个组合去做试验,这里n一般远小于pf。我们以正交表L9(33)为例,对3因素、3水平的问题而言,若依据正交表L9(33)来进行正交试验,只需做9次试验,但若进行全面组合试验,则需33=27次试验。可见正交试验设计大大减少了试验次数,且因素和水平越大,该方法的优越性越明显。
本文需要优化的因素有3个:x1,x2,x3,分别对应复合材料导条的结构尺寸br1,合金材料的电导率倍数σr/σr0和磁导率倍数μr/μ0,每个因素取3个水平,如表1所示。

表1 试验因素及水平Table 1 Factors and levels
设计3因素3水平的正交表进行试验,利用有限元法计算得到不同变量组合条件下的各项性能指标,包括堵转转矩倍数、堵转电流倍数和永磁体最低工作点磁密,结果如表2所示。

表2 正交试验设计及结果Table 2 Orthogonal experimental design and results
3 二次响应面回归模型
二次响应面回归模型具有统计学意义[11-13],利用正交试验的计算结果拟合各项性能指标的二次响应面回归方程。式(2)为拟合的堵转转矩倍数Tst,堵转电流倍数Ist,以及永磁体最低工作点磁密Bmin的二次响应面回归方程。将用于遗传算法目标函数的构造。

4 遗传算法的目标优化
遗传算法是一种基于自然选择原理和自然遗传机制的搜索(寻优)算法,它模拟自然界中的生命进化机制,实现特定目标的优化。遗传算法以其全局寻优方面的优势,在电机优化设计中已得到广泛应用[14-17]。其基本思想是将问题空间中的决策变量通过一定编码方法表示成遗传空间的一个个体,同时,将目标函数值转换成适应值,它用来评价种群中个体的优劣,并作为遗传操作的依据。遗传操作包括三个算子:选择、交叉和变异。遗传算法通过遗传中的选择、交叉及变异对个体进行筛选,使适应度高的个体被保留下来,组成新的群体,新的群体既继承了上一代的信息,又优于上一代。这样周而复始,群体中个体适应度不断提高,直到满足某种收敛指标为止。
使用遗传算法需要决定的运行参数有:编码串长度、种群大小、交叉和变异概率。编码串长度由优化问题所要求的求解精度决定。种群大小表示种群中所含个体的数量,一般取种群数目为20~100。交叉概率Pc控制着交叉操作的频率,一般取0.4~0.99。变异概率Pm一般取0.000 1~0.1。遗传算法常采用的收敛判据有:规定遗传代数;连续几次得到的最优个体的适应值没有变化或变化很小等,本文采取后者。遗传算法流程图如图5所示。
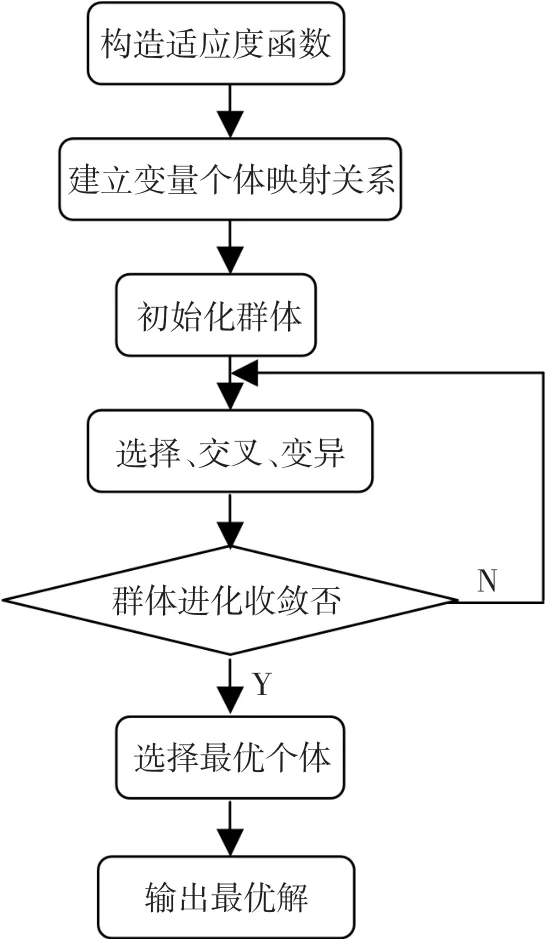
图5 遗传算法流程图Fig.5 Genetic algorithm flowchart
电机优化设计是一个多极值有约束的非线性问题。遗传算法对约束的处理有两种思路:一种是增加修正算子将约束条件反映在遗传算子的设计中;另一种是利用惩罚函数法将目标函数和电机的性能约束条件相结合,把有约束最优化问题转化成无约束的极值问题,在电机优化设计中常采取后者。由于自起动永磁电机起动过程中会出现最低工作点磁密[6],永磁体面临退磁的危险,从而影响电机性能。因此本文以永磁体最低工作点磁密Bmin为目标,以堵转转矩倍数Tst,堵转电流倍数Ist为约束条件,引入适当的罚函数法,构造增广目标函数F(X)为

其中,Tst0,Ist0分别为本文复合材料导条永磁电机的堵转转矩倍数和堵转电流倍数的约束值,分别取Tst0=3.36,Ist0=9.5;ω1,ω2为罚因子。
罚因子的选取至关重要,选择过小可能使最终结果不满足设计要求,过大又会影响优化设计的进程,甚至丢失最优方案。本文根据经验选取了合理的罚因子,在不影响设计结果准确性的前提下,使最终优化结果在可行域内。
本文进行遗传算法操作,选取交叉概率Pc=0.7,变异概率 Pm=0.011 7,求取增广目标函数F(X)的最大值。目标函数最大值和种群均值的收敛状况如图6所示。

图6 目标函数最大值和种群均值的收敛状况Fig.6 Convergence states of the maximum and average of the objective function
最优目标运行结果为:堵转转矩倍数Tst=3.62,堵转电流倍数Ist=8.94,永磁体最低工作点磁密Bmin=0.280 6 T。此时最优目标对应的设计变量为复合材料导条尺寸br1=2 mm,铜铁合金材料电导率σr=σr0以及磁导率μr=30μ0。采用优化后复合材料导条的永磁电机,与普通铸铝导条自起动永磁电机相比,如表 3所列数据,堵转转矩提高了7.74%,堵转电流降低了27.26%,永磁体最低工作点磁密提高了35.29%,实现了优化的目的。
5 结语
本文采用时步有限元法分析了复合材料导条的尺寸变量和合金材料电磁特性变量对永磁电机性能的影响,利用正交试验得到了不同变量组合条件下电机的各项性能指标,并利用正交试验结果拟合出堵转转矩倍数、堵转电流倍数及永磁体最低工作点磁密的二次响应面回归方程,采用遗传算法以抗退磁能力为优化目标,堵转转矩倍数和堵转电流倍数为约束条件进行全局寻优,使得采用优化后复合材料导条的永磁电机具有较优的起动性能和较高的抗退磁能力。
[1]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997:193-206.
[2]刘立恩,何代光.稀土永磁同步电动机异步软起动研究[J].电机与控制应用,2008,35(2):11 -13.
LIU Li’en,HE Daiguang.Research of asynchronous soft start of rare earth permanent magnet synchronous motor[J].Electric Machines & Control Application,2008,35(2):11 -13.
[3]刘新华,韩雪岩,唐任远,等.永磁同步电动机新型转子槽形设计[J].沈阳工业大学学报,2005,27(3):274 -276.
LIU Xinhua,HAN Xuanyan,TANG Renyuan,et al.Design on a new kind of rotor slots in permanent magnet synchronous motors[J].Journal of Shenyang University of Technology,2005,27(3):274-276.
[4]谭魏.新型节能电机起动及运行性能的数值分析[D].北京:华北电力大学电气与电子工程学院,2005:33-42.
[5]刘明基,卢伟甫,宋中阳,等.一种具有复合材料起动导条的自起动永磁电机:中国,CN102111051B[P].2012-11-21.
[6]卢伟甫,刘明基,罗应立,等.自起动永磁同步电机起动过程退磁磁场的计算与分析[J].中国电机工程学报,2011,31(15):53-60.
LU Weifu,LIU Mingji,LUO Yingli,et al.Demagnetization field analysis and calculation for line-start permanent magnet synchronous motor during start process[J].Proceedings of the CSEE,2011,31(15):53-60.
[7]卢伟甫,罗应立,赵海森.自起动永磁同步电机起动过程电枢反应退磁分析[J].电机与控制学报,2012,16(7):29 -33.
LU Weifu,LUO Yingli,ZHAO Haisen.Armature reaction demagnetization analysis for line-start permanent magnet synchronous motor during start process[J].Electric Machines and Control,2012,16(7):29-33.
[8]蔡自兴,江中央,王勇,等.一种新的基于正交试验设计的约束优化进化算法[J].计算机学报,2010,33(5):855 -864.
CAI Zixing,JIANG Zhongyang,WANG Yong,et al.A novel constrained optimization evolutionary algorithm based on orthogonal experimental design [J].Chinese Journal of Computers,2010,33(5):855-864.
[9]LEUNG Yiuwing,WANG Yuping.An orthogonal genetic algorithm with quantization for global numerical optimization[J].IEEE Transactions on Evolutionary Computation,2001,5(1):41 -53.
[10]WANG Wei,WANG Qingnian,ZENG Xiaohua,et al.Parameter matching of induction motor for electric vehicle based on orthogonal design[C]//Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation,August 9 - 12,2009,Changchun,China.2009:1455 -1459.
[11]CHOI Jaehak,KIM Taeheoung,JANG Kibong,et al.Geometric and electrical optimization design of SR motor based on progressive quadratic response surface method [J].IEEE Transactions on Magnetics,2003,39(5):3241 -3243.
[12]仇丽霞,刘桂芬,何大卫,等.二次响应面回归模型用遗传算法探索最优试验条件[J].中国卫生统计,2004,21(4):194-197.
QIU Lixia,LIU Guifen,HE Dawei,et al.The best experimental condition based on genetic algorithm for the quadratic response surface regression model[J].Chinese Journal of Health Statistics,2004,21(4):194 -197.
[13]张丕德,郜艳辉,李丽霞,等.对数优势二次响应面回归及其应用[J].数理医药学杂志,2006,19(3):313 -314.
ZHANG Pide,GAO Yanhui,LI Lixia,et al.Quadratic response surface regression models of log odds and its application[J].Journal of Mathematical Medicine,2006,19(3):313 -314.
[14]UlER G F,MOHHED O A,KOH C S.Utilizing genetic algorithms for the optimization design of electromagnetic devices[J].IEEE Transactions on Magnetics,1994,30(6):4296 -4298.
[15]CHO Donghyeok,JUNG Hyunkyo,CHUNG Taekyung,et al.Design of a short-time rating interior permanent magnet synchronous motor using a niching genetic algorithm [J].IEEE Transactions on Magnetics,2000,36(4):1936 -1940.
[16]李辉,许艮,杨超,等.汽车天窗电机设计参数对齿槽转矩影响及优化[J].电机与控制学报,2012,16(1):18 -22,30.
LI Hui,XU Gen,YANG Chao,et al.Influences of design parameters on cogging torque and optimization of low noise sunroof motor[J].Electric Machines and Control,2012,16(1):18 -22,30.
[17]吕德刚.改进自适应遗传算法在防爆高能电机优化设计中的应用[D].哈尔滨:哈尔滨理工大学电气与电子工程学院,2007:16-35.

