直流变换器模式快速识别PI自适应控制策略
谢桢, 付立军, 肖飞, 王瑞田
(海军工程大学舰船综合电力技术国防科技重点实验室,湖北武汉 430033)
0 引言
由于多电平拓扑能够解决开关管功率和耐压的约束,故可以用于实现高压大功率电能变换装置,目前已广泛运用于中高压大功率交流传动,高压直流输电等领域[1-2]。为了实现中压直流电网至低压直流电网的能量传送,本文提出了一种带隔离的三电平H桥直流变换器方案。针对工频下隔离变压器体积重量较大的问题,变换器采用PWM移相控制,以提高变换器工作频率,减小变压器体积重量。本文在H桥输出电压谐波分析的基础上设计了变换器的静态工作点,并建立了电流连续模式(CCM)和电流断续模式(DCM)下的数学模型,仿真计算结果表明在不同模式下变换器的动态性能差异较大,传统的PI控制方案难以满足变换器全负载范围内的较好动态性能,需要寻找更优的控制策略。
目前对直流变换器控制策略的研究多集中于一种工作模式设计控制器[3-5],没有考虑模式切换所引起的扰动。而针对全模式工况,则以非线性控制策略为主,例如滑膜控制器[6],单周期非线性控制器[7],基于反馈线性化设计的非线性控制器[8-9],但均存在计算量较大,难以用于工程实践的问题。大部分全工作模式控制器需检测模式状态,一般采用检测电感电流过零点或者电感电流峰值[10]的方法。而无传感器的模式识别策略也有文献提出[11],但其准确率存在限制。
在总结前述直流变换器控制策略研究的基础上,本文提出了一种基于CCM/DCM模式快速识别的PI自适应非线性控制策略。相比于传统PI控制方法,该控制策略的基本思路是基于电感电压特征,对系统工作模式快速辨识,然后根据模式变化实时调整控制器参数以达到最佳的控制性能。最后通过实验验证了该控制策略的可行性和有效性。
1 三电平H桥直流变换器
三电平H桥直流变换器的主电路结构如图1所示。输入直流电压为Ud,P点为直流源正极,N点为直流源负极,O点为中点,输出直流电压为uo,前端Cd1和Cd2为直流分压电容,容值相等,其后为二极管钳位三电平H桥结构,G1~G8为IGBT,D1~D8为反并联二极管,Dc1~Dc4为钳位二极管,Dr1~Dr4为整流二极管,L1为和L2滤波电感,Co为滤波电容,输出直流电流为io。H桥输出通过中频变压器降压后,由不控整流桥整流并经LCL滤波器滤波输出到下级电网。
中点钳位三电平H桥的输出电压uT1的波形如图2所示。其中基准桥臂电压为uao,滞后桥臂电压为ubo,α为移相角,θ为导通角,γ为钳位角(γ=π -θ),开关频率为 fS,角频率为 ωS,开关周期为TS。γ,α 和 θ记为占空比的形式为 dγ=γ/2π,dα=α/2π 和 dθ=θ/2π。
变换器在实际工作过程中要求uT1的基波幅值较大,且THD尽可能小,这样有利于将能量通过脉冲变压器传送到后端不控整流桥。因此在谐波分析的基础上可确定系统静态工作点为:dθ=0.42,dα=0.348。

图1 三电平H桥直流变换器的主电路拓扑Fig.1 The topology of the three-level H-bridge converter

图2 三电平H桥移相PWM调制下的输出电压波形Fig.2 The voltage waves of three-level H-bridge with phase-shift control
2 CCM/DCM模式下变换器的数学模型
1)模型假设
建模前假设:系统在静态工作点附近稳定运行;功率管等效为理想开关;L2主要影响系统的高频特性,对系统动态过程建模可忽略其影响。基于假设,可得到变换器的简化电路模型如图3所示,其中变压器原边漏感为Lr,变压器励磁电感为Lm,变压器变比为NT,滤波电感电流记为iL,滤波电感电压记为uL,变压器原边电流记为iLr。设系统的状态方程为=Ax+Bu,其中状态变量为x=[iLuo]T,输入变量为 u=[ud]。

图3 变换器简化电路模型Fig.3 The simplified circuit model of the converter
2)CCM模式下变换器的数学模型
基于CCM下系统模态分析,由状态空间平均法可得系统的状态空间平均方程为
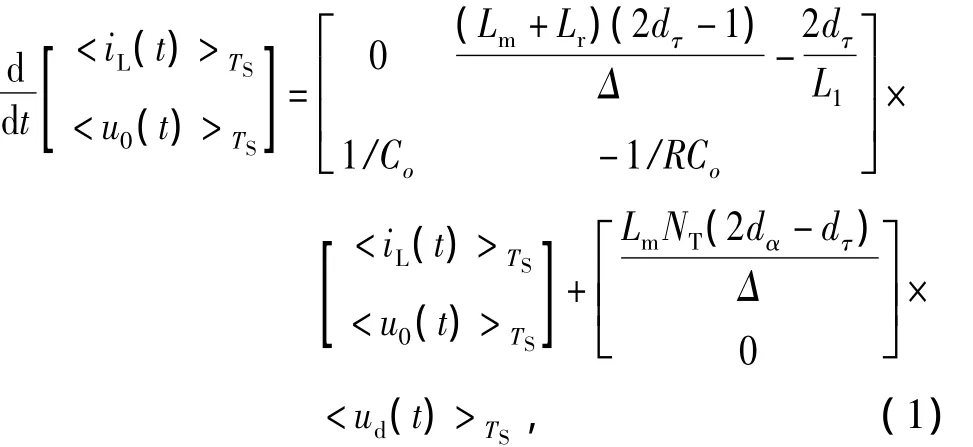
其中:Δ=L1Lr+L1Lm+LmLr;dτ称为丢失占空比,即当uT1从0开始翻转时,由于漏感Lr存在,变压器原边电流iLr不能突变,而是存在一个反向过程,直至重新建立起变压器的磁场,这段时间变压器原边的能量没有传递到副边,导致副边电压的有效值减小,故dτTS为占空比丢失时间。其解析表达为

采用扰动法求解小信号模型为

其中状态矩阵、输入和输出矩阵分别为
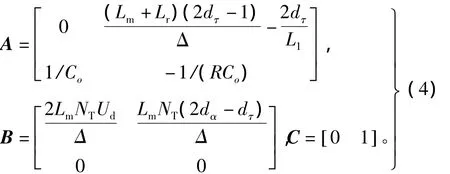
小信号模型框图如图4所示。

图4 小信号模型系统(CCM)Fig.4 The small signal model(CCM)
3)DCM模式下变换器的数学模型
基于DCM下系统模态分析,由开关网络平均法可得DCM模式下小信号模型为

其中,r2和k2为模型参数,根据负载轻重不同,DCM模式又可以分为DCM1模式和DCM2模式,具体的模型参数解析表达式为

小信号模型框图如图5所示。
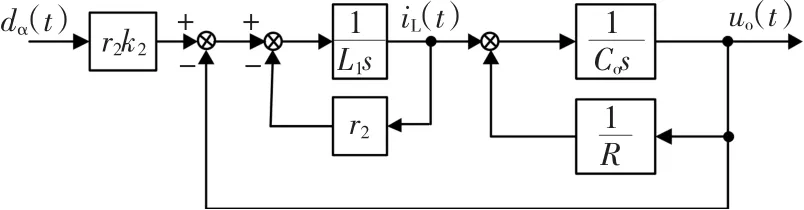
图5 小信号模型系统(DCM)Fig.5 The small signal model(DCM)
4)数学模型特性分析与验证
为了分析变换器的动态特性和验证小信号模型的正确性,基于仿真平台Matlab/SIMULINK进行了仿真研究。电路参数设为:Ud=4 000 V,Uo=710 V,Ts=1 ms,L1=250 μH,Co=5 mF,L2=50 μH,Lm=127.3 mH,Lr=51 μH,NT=0.263,dθ=0.42,dα=0.348。分别取 R=9.601 4 Ω(7%负载,DCM 模式),和 R=0.672 1 Ω(100%负载,CCM 模式)。
将电路参数代入仿真模型和数学模型,若仿真电路仿真计算得到的计算结果与数学模型计算得到的计算结果吻合,则验证了小信号数学模型的正确性。对比仿真模型和数学模型的动态计算结果如图6(a)和(b)所示。图6(a)中,t=0.08 s时刻,移相占空比dα突加10%扰动,图中所示输出电压uo的变化反映出CCM模式下小信号模型的动态响应和仿真模型的动态响应基本吻合;图6(b)中,t=0.1 s时刻,dα突加10%扰动后uo的动态反映出DCM模式下小信号模型的正确性。

图6 不同模式下小信号模型的验证Fig.6 The verify of the small-signal models by simulation
如图6所示和前述建模过程分析,变换器在CCM和DCM工作模式时的动态性能差别较大,CCM模式时的系统阻尼明显小于DCM模式,基于其中任何一种模式设计的电流电压双闭环PI控制器都可能在另外一种工作模式下得不到较好的动态性能。即基于传统方法设计的控制系统应对模式切换这种大扰动时控制性能较差。
3 PI自适应非线性控制策略
若能快速检测出系统处于何种工作模式,则可以通过实时调整控制器参数来适应系统的动态扰动,所以提出一种基于CCM和DCM模式快速检测的PI自适应控制器。
根据移相PWM调制原理和变换器的工作原理,可以设计控制器框图如图7所示,控制器以电压电流双闭环PI控制为基础,输入电压参考指令为Uoref。考虑到变换器可能需要并联运行,采用输出阻抗法均分负载,设调差系数为KI,io经过下垂特性调整后,与Uoref相减得到最终电压指令值,再与输出电压uo比较,送入电压环PI自适应调节器运算,得到电感电流指令值ILref。ILref与iL比较后送入电流环PI自适应调节器运算,运算结果运算结果送入限流控制器。限流控制器的主要功能是利用滞环控制实现短路限流,限流控制器输出移相控制信号dα,经过移相PWM调制器得到脉冲控制信号。其中电压电流环PI自适应调节器的PI参数是根据CCM/DCM模式检测来实时调整的。

图7 模式快速识别PI自适应非线性控制策略Fig.7 Mode fast identification PI adaptive control method
4 基于电感电压特征的模式快速辨识方法
要实现上述控制器功能,其关键在于能够实现对CCM和DCM模式的快速识别,目前文献中提出的方法中多数是基于检测电感电流过零点,但实际工程中,由于传感器存在零偏,尤其是在较大电流等级的传感器,在小电流条件下是误差很大,几乎不能采样到电感电流过零点,同时比较电路也存在一定的误差,加上采样误差等因素,出现误检测的概率很大。因此本文提出一种基于电感电压特征快速识别CCM/DCM工作模式的检测方案,模式判别流程如图8所示,具体原理如图9所示,其中ur所示为整流桥输出。
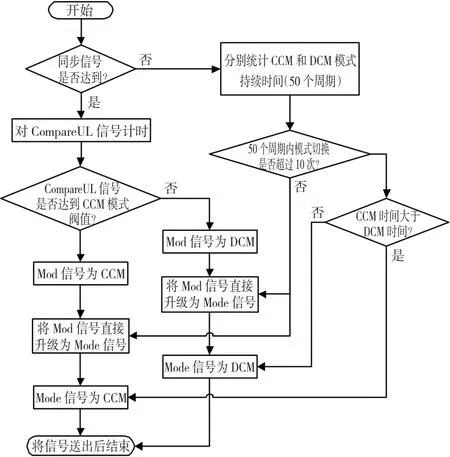
图8 基于电感电压特性模式判断流程Fig.8 The flow scheme of mode identification based on inductance voltage

图9 基于电感电压特性的模式快速识别示意Fig.9 The sketch of CCM/DCM fast identification based on inductance voltage
当DCM模式切换至CCM模式时,电感电流由断续变为连续,过零点消失,同时电感电压的变化也存在明显特征,即电感电压最高电平持续时间明显较CCM模式减少,而CCM模式下最高电平持续时间是固定的,具体如图9中uL所示。利用这一特性,可设计如图9所示的检测电路,该检测电路主要由外围比较电路和FPGA构成。其中比较电路将电感电压采样信号和零比较后得到的Cp-uL信号送入FPGA,FPGA根据同步时钟信号和PWMsyn同步逻辑信号对比较电路输出信号进行计时,根据计时长短判断出工作模式,输出Mod信号。
若只考虑稳态,则Mod信号已能够表征系统的工作模态,但是当系统受到诸如突加负载等大扰动时,Mod信号可能会发生连续变化,若Mod信号连续变化次数过多则可能导致系统输出振荡失稳。基于此考虑,在Mod信号生成后,送入模式信号多数表决强制稳定模块,进行模式信号的强制稳定,最终得到的Mode信号即为送出FPGA的模式信号。
5 实验验证
为了验证前述对变换器工作原理的分析,以及基于CCM/DCM模式快速识别的PI自适应非线性控制策略的有效性,搭建原理样机实验平台进行实验。实验原理样机采用RTLAB实时仿真系统和FPGA作为控制算法实现的主体,RTALB是一种国际上比较流行的实时仿真工具,可以构建速控制原型(RCP),将控制器与实际的控制对象构成闭环回路对控制算法进行验证[12-14]。
具体的实验样机参数为:Ud=500 V,Uo=166 V,Ts=1 ms,L1=2 mH,Co=420 μF,L2=0.4 mH,Lm=0.277 33 H,Lr=85 μH,NT=0.5。
图10和图11所示为实验样机控制性能实验波形。图10(a)和(b)所示为传统双闭环PI控制和基于CCM/DCM模式快速识别的PI自适应非线性控制的动态性能对比,其中通道C1为输出电压uo波形(100 V/div),通道C2为Mode信号(0.5 V/div),通道C3为电感电压uL波形(100 V/div),通道C4为PWMsyn信号(0.2 V/div)。图10(a)和(b)所示均为突加5.17 Ω负载(50%负载)时系统的动态响应,从Mode信号变化可看出基于电感电压特征的模式检测准确且速度较快,对比图10(a)和(b)中输出电压波形可得,采用传统双闭环PI控制,输出电压最大跌落为123 V,而采用本文提出的控制方法,则输出电压最大跌落为92 V,性能明显优化。图11所示为突加0.2838 Ω短路电阻时的短路限流控制波形,其中通道C1为输出电压uo(50 V/div),通道C3为移相控制输出dα(0.25/div),通道F1为输出电流io(134 A/div),从io波形可看出系统的短路限流控制功能得到验证。

图10 控制策略的实验验证(空载至50%负载)Fig.10 The verification of the control method by prototype(no load to 50%load)

图11 控制策略的实验验证(短路限流)Fig.11 The verification of the control method by prototype(current limited when short circuit)
6 结论
本文分析了一种带隔离的三电平H桥直流变换器,通过对变换器数学模型研究发现其在不同工作模式下的动态性能差异较大,因此提出一种基于CCM/DCM模式快速识别的PI自适应非线性控制策略,通过实验验证,可得到以下结论:
1)本文提出的基于电感电压特征快速识别CCM/DCM工作模式的方案,具有检测快速,易于实现,外围电路简单,抗干扰能力强等优点。而且易于推广到其他需要进行模式辨识的场合,例如两电平直流电路,有源滤波电路等。
2)本文提出的基于模式快速识别的PI自适应控制策略较之传统PI控制策略具有更优的控制性能。而且易于推广到其他需要全模式运行的直流变换器。
[1]STEFFEN Bernet.Recent developments of high power converters for Industry and traction application[J].IEEE Transaction on Power Electronics,2000,15(6):1102 -1117.
[2]王建渊,王琦,钟彦儒.一种用于三电平逆变器的双模式过调制策略[J].电机与控制学报,2012,16(6):30 -36.
WANG Jianyuan,WANG Qi,ZHONG Yanru.One strategy of two -model over modulation for three-level inverter[J].Electric Machines and Control,2012,16(6):30 -36.
[3]QIU Ying,CHEN Xiyou,LIU Helen.Digital average current-mode control using current estimation and capacitor charge balance principle for DC/DC converters operating in DCM[J].IEEE Transaction on Power Electronics,2010,25(6):1537 -1545.
[4]SREENU Kancherla,Ray Tripathi.Nonlinear average current mode control for a DC/DC Buck converter in continuous and discontinuous conduction modes[C]//IEEE TENCON,Hyderabad,Nov.2008:1-6.
[5]陈道炼,陈亦文,张灵改.差动Buck/Boost直流变换器型高频环节逆变器[J].电机与控制学报,2010,14(11):13 -19.
CHEN Daolian,CHEN Yiwen,ZHANG Linggai.Differential Buck/Boost DC/DC converter mode inverter with high frequency link[J].Electric Machines and Control,2010,14(11):13 -19.
[6]LIN Hungchih,CHANG Tsinyuan.Analysis and design of a sliding mode controller for Buck converters operating in DCM with adaptive hysteresis band control scheme[C]//IEEE 7th PEDS,Bangkok.Allahabad:IEEE Press,2007:372 -377.
[7]EGIZIANO L,FEMIA N,FORTUNATO M.Dynamic model of onecycle control for converters operating in CCM and DCM[C]//IEEE 32nd IECON,Paris,Nov.2006:2150 -2155.
[8]WU Jianhua,YANG Haitao,ZHANG Haixin.Model-free adaptive control for model mismatch power converters[C]//IEEE CCDC.Mianyang,China:IEEE Press,2011:1168 -1171.
[9]HADI Kanaan,KAMAL AlHaddad.A novel averaged-model-based control of a SEPIC power factor corrector using the input/output feedback linearization technique[C]//lEEE 36th PESC,Recife.2005:565-571.
[10]SHU Fan Lim,ASHWIN Khambadkone.A simple digital DCM control scheme for Boost PFC operating in both CCM and DCM[J].IEEE Transaction on Industry Applications,2011,47(4):1802-1812.
[11]JABER A,QAHOUW Abu.Control scheme for sensorless operation and detection of CCM and DCM operation modes in synchronous switching power converters[J].IEEE Transaction on Power Electronics,2011,25(10):2489 -2495.
[12]YE Xi.A PC-cluster based real-time simulator for all-electric ship integrated power systems analysis and optimization[C]//IEEE ESTS,Arlington VA,May.2007:396 -401.
[13]MESH Steurer.PEBB based high-power hardware-in-loop simulation facility for electric power systems[C]//IEEE Power Engineering Socirty General Meeting,Montreal Que,April.2006:1-3.
[14]REN Welter,QIAN L,LIU Y.Real time digital simulations augmenting the development of functional reconfiguration of PEBB and universal controller[C]//IEEE American Control Conference,Portland OR USA,April 2005:2005 -2010.

