三角函数的开关磁阻电机磁链解析模型
钟锐, 曹彦萍, 徐宇柘, 屈严, 彭富林
(1.东南大学国家ASIC系统工程研究中心,江苏南京 210096;2.东南大学电子科学与工程学院,江苏南京 210096)
0 引言
开关磁阻电机(switched reluctance motor,SRM)是一种双凸极无刷电机,其定子集中绕组,转子仅由硅钢片组成,具有不需要永磁材料,结构坚固、耐高温的优点,在油田和煤矿设备中得到广泛应用,且在国内外电动汽车中得到相当的重视和应用[1-2]。日本东京理工大学已经研发出50 kW开关磁阻电机应用于电动汽车;电产株式会社从2012年开始生产开关磁阻电机应用于重型机械和电动汽车,以减少电机对稀土材料的依赖性。
SRM驱动系统是转速和相电流的双闭环复杂控制系统,具有多参数、非线性、强耦合的特点。其核心部分-SRM电机本体,因为常工作在磁饱和状态下,所以其电—磁—机的能量转换过程尤为复杂,对SRM电机本体的磁链或电感等磁特性模型的研究一直方兴未艾[3]。
已有SRM电机ψ-i-θ磁链建模方法可主要分为下面几种:查找表法[3],有限元分析法(finite element analysis,FEA)[4],等效磁路分析法[5],三次样条插值法[6],解析模型法等[7-10],近年来还出现了人工智能法,如模糊逻辑、人工神经网络(artificial neural network,ANN)[11]和模糊—神经网络[12-13]等。上述方法中,等效磁路分析法和有限元分析法的计算过程极为复杂;三次样条插值法和查找表法均需要大量的磁链-相电流-转子位置数据以保证其精确度[14];而人工智能法虽然在泛化能力和精确度上较好,但其训练过程较长,实现难度也较大[9]。
解析法具有较高的精确度和计算速度[15-16],且更易于在工程中得到应用,因此,一直以来均有学者进行研究。文献[17]将SRM电机磁链模型描述为转子位置角度的一阶或二阶函数,并以此推出了快速转矩计算公式;文献[7]利用二阶插值法建立了i(θ,ψ)逆向查找表;文献[1]首先提出了 Spong模型,即采用指数函数来描述磁链;文献[8-9]对Spong模型相继进行了修改,增加了额外的转子位置项等方法来提高其精确度,降低了残差平方和(sum of squares for error,SSE)。
指数函数虽然与磁链模型形状较为接近,尤其能较好的反映定转子对齐位置附近磁链饱和区的非线性磁链参数,但其计算量较大。此外,指数函数是利用高斯核函数的变形进行曲线拟合,而高斯核函数的中心点选取方法的理论一直不成熟,影响了拟合精确度。因此文献[14]和文献[18]利用傅里叶级数建立了磁链模型关系,并分别采用Arctan(i)函数和Froelich函数描述傅里叶级数的系数,但文献[14]的转矩计算公式较难求解,而文献[18]的精确度较低;文献[10]提出了基于傅里叶级数的可逆磁链模型,该模型中的各系数由SRM电机的机械尺寸和硅钢片材料推导而来,但精确度仍不理想。
本文对基于三角函数的磁链模型进行了研究,以磁链-转子位置角度公式ψ-θ为基础,并采用以相电流为变量的多阶多项式作为不同频率下三角函数的各项系数,最终对FEA磁链数据族进行了拟合描述,使该磁链模型接近指数函数模型最好的结果,而同时转矩计算量大幅降低。
1 建模
模型是基于一个3相,12/8结构的SRM实验电机,额定功率1.28 kW,额定转速3 600 r/min,其截面图如图1所示。
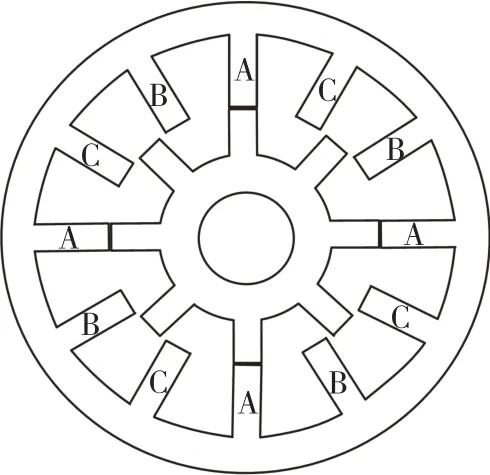
图1 3相SRM截面图Fig.1 The cross-section area of the investigated 3-phase SRM
1.1 磁链与转子位置关系
图2所示为通过FEA方法获得的实验电机某相的磁链-转子位置-相电流曲线族(ψ-θ-i),定转子凸极对齐位置设定为0°,非对齐位置设定为-22.5°和22.5°。
以往模型主要围绕如图2(a)中的磁链-相电流曲线族ψ-i进行讨论,该曲线族中接近对齐位置的几条曲线由于饱和程度高而非常接近。本文采用如图2(b)中所示的磁链-转子位置曲线族ψ-θ进行分析,以期借助磁链的轴对称性而获得更好的拟合效果。
磁链对转子位置曲线的对称性要求其模型是偶函数,具备此特性的函数容易想到是余弦函数,单个余弦函数不能表达如此丰富曲线簇,多个函数组合且能组成完备正交的函数形式是傅里叶级数,考虑到计算量及常见解析模型大多是4~5个参数,则试用下面公式表达磁链模型,包含了包括常量和1至4次谐波在内,形式为

其中:a0~a4是与相电流i有关的系数;ψ是相磁链;θ是转子位置角度。

图2 SRM磁链特性Fig.2 Flux linkages of SRM
式(1)与电流相关的参数有5个,减少其个数可减少计算量,也可降低系数拟合的难度。为此,需寻找a0~a4之间是否存在函数关系,利用实际样机数据拟合后,得到参数a0~a4,发现a3与a4存在线性关系,后者大约是前者的1/12,利用回归分析工具计算其相关系数为0.95,而高次谐波的影响程度较小,因此作近似处理为

等式(1)可简化为

等式(1)中的系数a0~a3通过基于Levenberg-Marquardt算法的最小二乘方法进行拟合,其结果分别如图3中所示。一般6阶多项式即可拟合任意曲线,考虑到精确度和计算量的折中,上述系数均采用易于秦九昭算法进行计算的6阶多项式形式表达,有

其中,cnj是an中各项的系数,再次采用最小二乘法计算得出其系数如表1中所示。
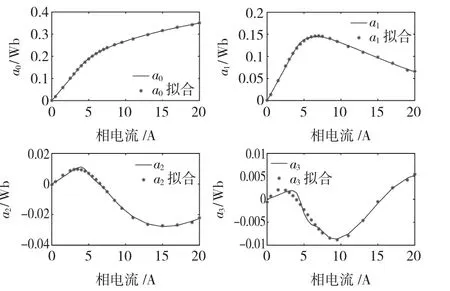
图3 系数a0,a1,a2和a3关于相电流的函数Fig.3 Coefficients a0,a1,a2and a3as functions of the phase current i
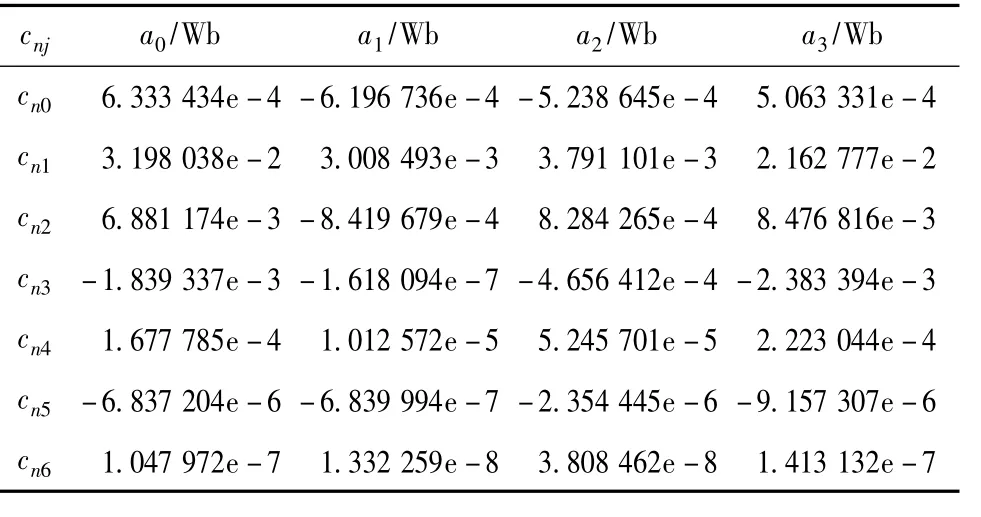
表1 等式(3)系数拟合多项式的系数Table 1 Polynomial coefficients used for fitting coefficients in equation(3)
至此,实验电机的磁链模型可由表1中的系数和等式(4)完整建立出来。该模型与FEA原ψ(i,θ)数据进行对比后的结果如图4中所示。

图4 FEA和本文模型生成的磁链对比Fig.4 Comparisons of flux linkage derived from proposed model and FEA results.
下面对该模型精确度进行进一步分析,采用误差平方和(sum squared error,SSE)函数进行量化,定义给定转子位置θk和相电流ij的SSE函数为

其中:ψ(ij,θk)为本文所建模型计算结果;ψjk为 FEA数据;n代表误差量化所选择的曲线族数,本文取值16。图5所示为相电流从0到20 A的SSE变化情况。最大 SSE为 6.209 3e-4 Wb2,平均 SSE为2.799 8e-4 Wb2。
1.2 转矩计算
以往建模方法在计算电机转矩时几乎都要采用近似函数的方法来降低计算复杂度例如文献[9]中其转矩公式无法积分,引入双曲正切函数来逼近其不可积分部分,从而会引入新的计算误差。本文所提出的方法则不需要做函数近似。
电机某相转矩可从磁共能W推导出来,有

其中,ia是相瞬时电流。将等式(3)代入式(6)可得
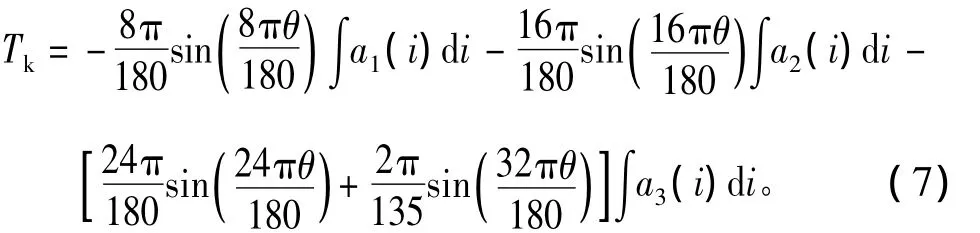
等式(7)中,系数an(i)是等式(4)中的6阶多项式,则∫an(i)di是一个6阶多项式的积分,是完全可积的,且结果仍是多项式,仍可用秦九昭算法简化计算。因此,其计算过程非常简洁,转矩的计算量很小。避免了采用其他函数再次逼近转矩计算过程引入新误差。
图6所示为实验SRM电机在不同相电流下的转矩仿真波形。其结果与FEA仿真出的转矩结果较为符合。

图6 FEA和本文模型转矩对比Fig.6 Comparison of torques between the FEA and the proposed model
1.3 模型比较
下面将本文所提出的模型与 Torrey模型和Chen模型进行精确度和计算量上的比较,其结果如表2和表3所示。

表2 现有模型核本文提出模型磁链误差对比Table 2 Comparisons of flux linkage accuracy of the existing models and the proposed model

表3 现有模型和本文提出模型转矩计算量对比Table 3 Comparisons of torque calculation cost of the existing models and the proposed model
从表2中可以看出,本文所提模型的SSE比Torrey模型要小一个量级,最大SSE和平均SSE分别是Torrey模型的15.5%和19.0%;比Chen模型略差,最大SSE和平均 SSE分别是 Chen模型的142.2%和160.0%,但同样在较高精确度的范围内。由表3可知,在计算量方面,本文所提模型在进行转矩计算时,其乘和加操作分别是Torrey模型的67.23%,Chen模型的38.83%。综合精确度和计算量两个指标,本文所提模型的方法保持高精确度情况下,大大减小了计算量。
需要说明的是,尽管等式(3)是根据3相12/8结构的SRM电机建立的,但是该等式同样适用于具备单极对称结构的其它相数和极数的SRM,只是多项式系数an需要根据SRM具体参数重新调整。
2 仿真和实验结果
2.1 实验硬件环境
图7所示为基于Matlab/SIMULINK所建立的SRM驱动仿真系统框图。实际转速ω与整定转速ω'之间的转速差值Δω提供给速度控制模块(speed controller)以计算参考相电流iref;角度控制模块(APC controller)计算开通角 θon和关断角 θoff;功率管驱动模块(gate driver)根据换相信号来产生功率管的栅驱动信号,并通过电流控制模块(current controller)的反馈信号产生斩波信号。SRM电机由功率变换器模块驱动。

图7 SRM驱动系统框图Fig.7 Block diagram of SRM drive system
实验系统如图8所示。采用了ARM Cortex M3内核的STM32F103VBT6作为主芯片,功率变换器为典型不对称半桥结构。负载为20 N·m磁滞测功机,相电流采样元件为霍尔电流传感器。

图8 SRM驱动系统实验平台Fig.8 Experimental system of SRM driver
2.2 控制模式
2.2.1 角度控制(angular position control,APC)模式图9所示为空载、角度控制模式下的单相电流及栅驱动信号仿真波形和实测波形。开通角和关断角分别设置为-22.5°和-15°。相电压为270 V,电机转速稳定在3 000 r/min。通道1、2和3分别指示转子位置角度、栅驱动信号和相电流。

图9 空载、角度控制模式下的仿真和实测波形(3 000 r/min,θon= -22.5°,θoff= -15°)Fig.9 Simulated and measured waveforms without load under APC control(3 000 r/min,θon= -22.5°,θoff= -15°)
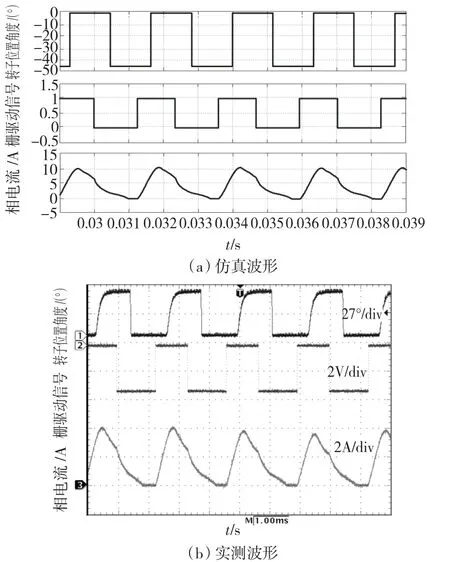
图10 负载3.5 N·m,角度控制模式下的仿真和实测波形(3 000 r/min,θon= -30°,θoff= -9°)Fig.10 Simulated and measured waveforms with 3.5 N·m load under APC control
图10所示为负载为3.5 N·m时的单相电流及栅驱动信号仿真波形和实测波形。开通角和关断角分别设置为-30°和-9°,相电压为270 V,电机转速稳定在3 000 r/min。
根据图9和图10的波形对比,可以看出,以所建模型为核心的仿真结果与实际电机测试结果有较好的一致性。
2.2.2 电流斩波控制(current chopping control,CCC)模式
图11所示为电流斩波控制模式(CCC)下的仿真和实测波形。该模式下的电流变化比较剧烈,更能反映模型的精确度,特别是在斩波时间点和持续时间等方面。负载为3.5 N·m,开通和关断角分别设置为 -22.5°和 -7.5°,相电压为270 V,电机转速稳定在1 000 r/min。斩波次数和时间一致性很好。
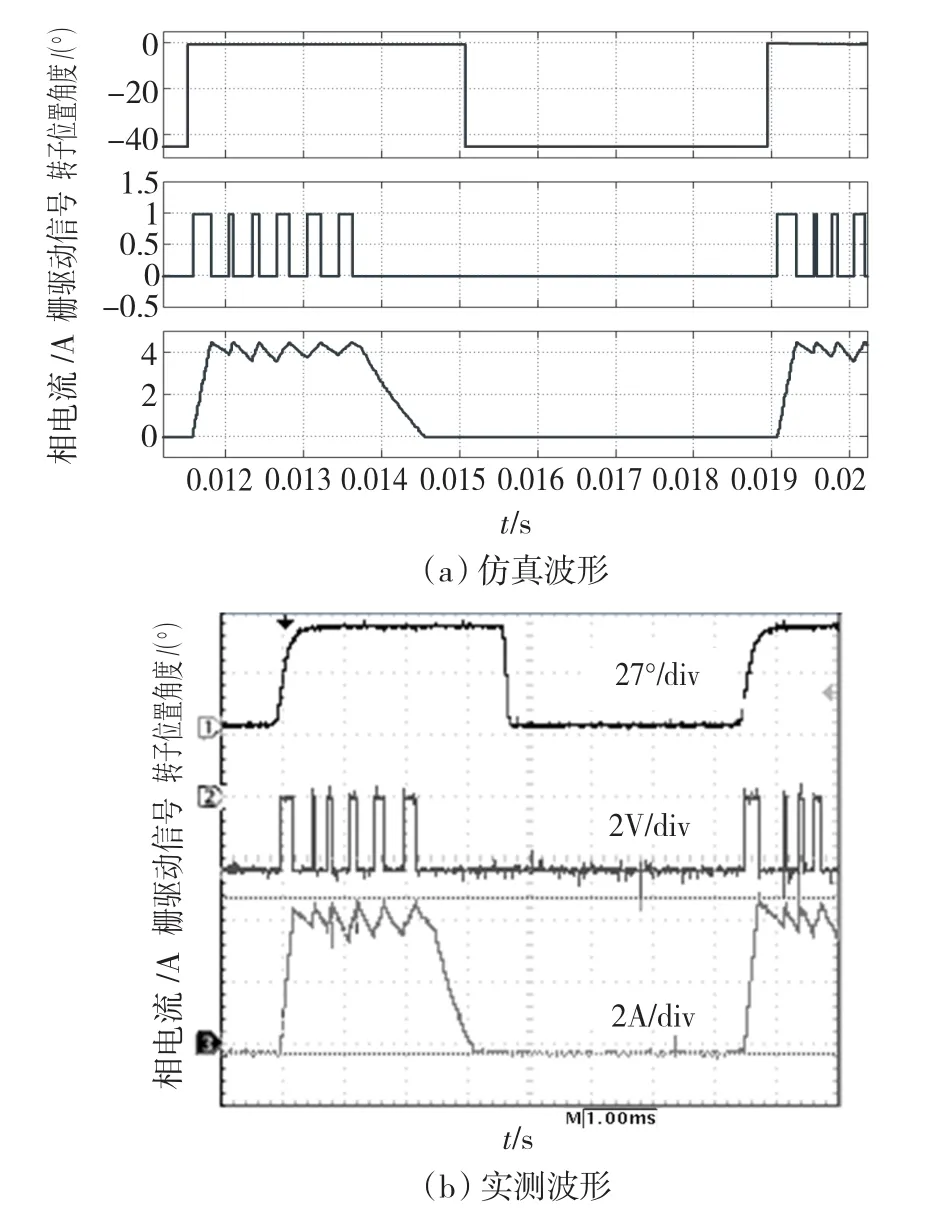
图11 负载1.5 N·m,角度控制模式下的仿真和实测波形(1 000 r/min,θon= -22.5°,θoff= -7.5°)Fig.11 Simulated and measured waveforms with 1.5 N·m load operation
2.3 计算量
电机相转矩的计算由STM32F103VBT6完成,该处理器在72 MHz主频下的定点计算性能达到90MIPS Dhrystones。由于计算公式中的数据大量是浮点型的,因此采用了坐标旋转数字计算算法(coordinate rotation digital computer,CORDIC)和浮点转换定点算法来提高计算速度。最终,磁链ψ和转矩Te的计算时间分别达到了60 μs和187 μs。一般来说SRM控制中,无需在一个周期内计算磁链和转矩,而即使电机在10 000 r/min时,一个周期45°是750 μs,磁链和转矩的计算时间足够适用于SRM电机的实时控制。如果电机需工作在超高速度,则可采用FPGA等硬件方案提高运算速度。
3 结语
根据磁链对转矩位置曲线簇的对称性特点,提出了一种基于三角函数的磁链-转子位置角度(ψ-θ)解析模型,其系数是关于电流的6阶多项式函数,并采用Levenberg-Marquardt算法的最小二乘方法求解出系数。由此磁链模型推导出的转矩公式是三角函数与多项式积分的乘积,多项式是可积分的,其计算过程非常简洁不需要再次近似。模型计算出的磁链和转矩同FEA方法得到的数据有很好匹配,同现有模型对比其特点是精确度较高的同时转矩减少了一半的计算量。在斩波控制模式和角度控制模式验证中,仿真与实测结果一致性好。实际计算量测试中,磁链和转矩公式的运行时间在72 MHz主频的 STM32 上为 60 μs和 187 μs,远小于SRM在10 000 r/min的一个周期,适用于在SRM电机控制中对磁链和转矩做实时解算。
[1]SPONG M,PERESADA S,TAYLER D.Feedback linearizing control of switched reluctance motors[J].IEEE Transactions on Automatic Control,1987,32(5):371 -379.
[2]KRISHNAN R.Switched reluctance motor drives:modeling,simulation,analysis,design,and applications[M].NewYork:CRC Press,2001:10 -20.
[3]SOARES F,BRANCO P J C.Simulation of a 6/4 switched reluctance motor based on Matlab/Simulink environment[J].IEEE Transactions on Aerospace and Electronic,2001,37(3):989-1009.
[4]SADOWSKY N,LEFEVRE Y,NEVES C G C,et al.Finite elements coupled to electrical circuit equations in the simulation of switched reluctance drives:attention to mechanical behavior[J].IEEE Transactions on Magnetics,1996,32(4):1086 -1089.
[5]KAKERNAK J M,TORREY D A.Magnetic circuit model for the mutually coupled switched reluctance machine[J].IEEE Transactions on Magnetics,2000,36(2):500-507.
[6]PULLE D W J.New database for switched reluctance drive simulation[J].Electric Power Applications,IEE Proceedings B,1991,138(6):331-337.
[7]STEPHENSON J M,CORDA J.Computation of torque and current in doubly salient reluctance motors from nonlinear magnetisation data[J].Electrical Engineers,Proceedings of the Institution,1979,126(5):393-396.
[8]TORREY D,LANG J H.Modeling a nonlinear variable-reluctance motor drive[J].Electric Power Applications,IEE Proceedings B,1990,137(5):314-326.
[9]CHEN H J,JIANG D Q,YANG J,et al.A new analytical model for switched reluctance motors[J].IEEE Transactions on Magnetics,2009,45(8):3107 -3113.
[10]KHALIL A,HUSAIN I.A fourier series generalized geometrybased analytical model of switched reluctance machines[J].IEEE Transactions on Industry Applications,2007,43(3):673-684.
[11]杨先有,易灵芝,段斌,等.开关磁阻电机调速系统BP神经网络建模[J].电机与控制学报,2008,12(4):447-450.
YANG Xianyou, YI Lingzhi, DUAN Bin, et al.Modeling switched reluctance driving with the BP neural network[J].E-lectric Machines and Control,2008,12(4):447-450.
[12]LIANG D,DING W.Modeling and predicting of a switched reluctance motor drive using radial basis function network-based adaptive fuzzy system [J].IET Electric Power Applications,2009,3(3):218-230.
[13]许爱德,樊印海,李自强.基于GA-ANFIS的开关磁阻电机建模[J].电机与控制学报,2011,15(7):54-59.
XU Aide,FAN Yinhai,LI Ziqiang.Modeling of switched reluctance motor based on GA-ANFIS[J].Electric Machines and Control,2011,15(7):54 -59.
[14]CHI H P,LIN R L,CHEN J F.Simplified flux-linkage model for switched-reluctance motors[J].IEE Proceedings of Electric Power Applications,2005,152(3):577-583.
[15]裴丽娜,葛宝明,毕大强,等.高速开关磁阻电机电磁解析分析方法[J].电机与控制学报,2010,14(9):48-54.
PEI Lina,GE Baoming,BI Daqiang,et al.An analytical method for electromagnetic performance of high-speed switched reluctance motor[J].Electric Machines and Control,2010,14(9):48-54.
[16]陈琼中,孟光,莫雨风.开关磁阻电机的精确转矩解析模型及Dymola的动态仿真[J].电机控制与应用,2008,35(10):14-20.
CHEN Qiongzhong,MENG Guang,MO Yufeng.An analytical precise torque model of switched reluctance machine and its dynamic simulation based on dymola[J].EMCA,2008,35(10):14-20.
[17]MILLER T J E.Nonlinear theory of the switched reluctance for rapid computer-aided design [J].Electric Power Applications,IEE Proceedings B,1990,137(6):337-347.
[18]LIN R L,CHEN J F,et al.Spice-based flux-linkage model for switched reluctance motors [J].Electric Power Applications,IEE Proceedings,2005,152(6):1468 -1476.

