一种高可靠电压均衡电路

0 引言

分布式直流电网，特别是分布式微型直流电网，是一种新型、灵活的低压直流传输系统，能够有效地将各种新能源(太阳能、风能、燃料电池等)以及各种储能单元(电池、超级电容等)有机地组网，并直接向用户提供高质量的电能［1－7］。

而微型直流电网通常采用两根输电线，只有一个等级直流电压。然而，用户端的用电设备却是多样的，不同的用电设备对输入电压的要求也不同，例如，半桥变换器需要输入电压平衡、低输入电压用电设备、高压输入用电设备等。所以只有一个电压等级的微型直流电网，无法满足不同用电设备对输入电压的要求。在微型直流电网中构造一根中线，满足不同用电设备对输入电压的要求;特别是与大地相连接的中线极大提高了微型直流电网安全性。因此，文献［4－7］将半桥电压均衡器引入微型直流电网。

由于半桥拓扑结构存在直通的危险，这影响其可靠性。近年来，一种可以避免直通危险的双降压结构被广泛的研究［8－10］。结合电压均衡器特点，本文研究一种基于双降压结构的高可靠电压均衡电路及其控制策略。

1 高可靠电压均衡电路和控制策略

典型的利用半桥电压平衡电路构造中线的微型直流电网如图1所示。

图1 一种典型带均衡微型直流电网构架Fig．1 A DC grid with voltage balancing circuit

由于图1中半桥结构中存在功率开关管直通问题，因此提出一种高可靠电压均衡电路如图2所示。它由左桥臂(S1、D1、L1)和右桥臂(S2、D2、L2)组成。为了适应该电路结构特点，希望左、右两个桥臂能够独立工作，即:1)电流＞，左桥臂工作向电阻负载RLoad2传递部分能量，电感电流平均值等于(－);2)当电流＞，右桥臂工作向电阻负载RLoad1传递部分能量，电感电流平均值等于(－)。

图2 高可靠电压均衡电路Fig．2 Voltage balancing circuit with a high reliability

为了实现上述目的，提出了如图3所示控制策略:调节器输出信号ue直接控制左桥臂，取反后(－ue)控制右桥臂。由于采用单极性调制三角波，所以当＞时左桥臂工作，右桥臂不工作;反之右桥臂工作，左桥臂不工作。由于两个桥臂之间串联两只电感，所以在左右桥臂切换瞬间不存在开关管直通问题，从而具有较高的可靠性。

图3 控制原理框图Fig．3 Presented control scheme

2 基本工作原理

为了简化分析，假设所有器件均是理想的，并且电容C1=C2=C、电感L1=L2=L。由于左桥臂与右桥臂工作过程类似，所以下面仅分析左桥臂工作过程。

2.1 左桥臂工作过程

根据电感电流情况，工作过程分为电感电流连续(CCM)和断续(DCM)模式，如图4所示。ugs1、ugs2分别是S1和S2驱动信号。

图4 电流连续和断续驱动和电流波形Fig．4 Driving and current iL1under CCM and DCM

2.1.1 电感L1电流连续

该模式下主要波形和各个模态等效电路如图4(a)和图5所示。

模态1:［t0－t1］［S1导通、S2关断，图4(a)和图5(a)］

在t0时刻开通S1，电感L1电压uL1=uin－uout2=uout1，电流从某个大于零开始线性上升。该过程持续到t1时刻关断S1，电流iL1达到最大值。

在这一过程中，输入电压uin利用电感L1向负载RLoad2传递部分电能。

模态2:［t1－t2］［S1、S2关断，D1导通，图 4(a)和图5(b)］

在t1时刻，关断S1。电流iL1通过二极管D1续流。在这一过程中，电感电压=－uout2，电流线性下降。该过程持续到t2时刻开通S1。从t2时刻，电路进入下一个工作周期。可见D1是强制关断。由于稳态时电压uout1=uout2，所以电流上升率和下降率相等。

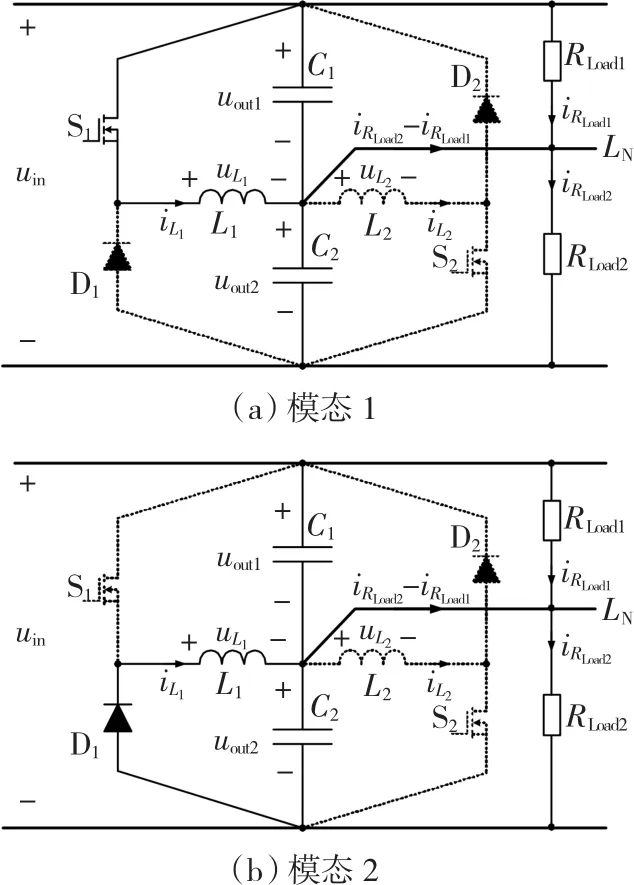
图5 电流iL1连续等效电路图Fig．5 Equivalent circuits under CCM

2.1.2 电感L1电流断续

电感电流断续时驱动和电流波形如图4(b)所示。在该模式下(t0－t1)和(t1－t2)两个时间内，由于电感L1电流非零，所以这两个时间内的两个工作模态与电流连续时两个模态工作过程相同。因此，这两个模态分析过程在此忽略。下面只给出在时间(t2－t3)内模态3等效电路和分析过程。

模态3:［t2－t3］［S1、S2关断、D1截止，图 4(b)和图6］

在t2时刻，电感L1电流下降到零，D1自动关断。从此电感电流一直为零，并持续到t3时刻开通S1，进入下一个工作周期。

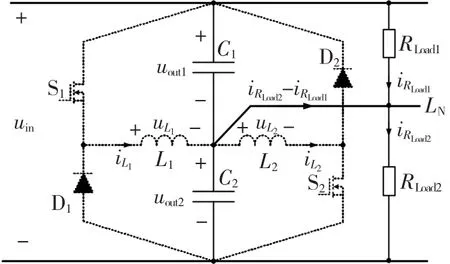
图6 电流断续模态3等效电路图Fig．6 Equivalent circuits of mode 3 under DCM

3 主要电流关系

电感和电容中的电流关系是设计电感和电容参数的重要基础。为了便于分析，将电路中各主要电流如图7所示，其中、是电容C1和C2电流，i1和i2是分别电容电流和负载电流之和。

图7 主要电流关系图Fig．7 Main current relationships

下面也仅以左桥臂为例分析其主要电流关系，其他情况与此类似，不再赘述。根据前面工作过程分析，可以得到如图8所示主要电流关系波形图。

图8 左桥臂工作主要电流关系波形图Fig．8 Main currents waveforms

3.1 电感L1电流非零期间主要电流关系

电感L1电流非零期间，如图8(a)和图8(b)中(t0－t2)时间所示。由于输出电压uout1、uout2之和等于uin，所以这两个电压是关联的，即uout2升高多少，uout1必然降低多少;反之，亦然。

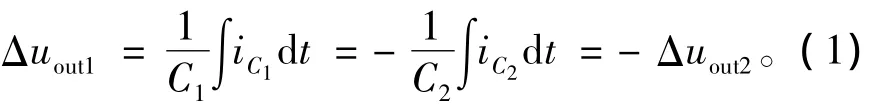
由于电流i1平均值等于负载电流iRLoad1，所以其脉动电流Δi1对C1充、放电，即电流=Δi1;同样，电流i2平均值也等于负载电流，其脉动电流Δi2对C2充、放电，即电流=Δi2。结合式(1)可得电流 Δi1、Δi2、和之间关系。

3.2 电感L1电流为零期间主要电流关系

4 小信号模型

为了控制系统参数设计和验证图3控制方案可行性，根据平均小信号模型建模方法［11］，建立平均小信号模型。

4.1 左桥臂小信号模型

由图7可得

1)S1导通

2)S1关断

设S1占空比为d1，并令d1=D1+，〈iL1〉Ts=+，〈uin〉Ts=Uin+，〈uout2〉Ts=Uout2+，其中，d^

1分别是扰动量;D1、Uin、Uout2分别是稳态分量。根据一周期内的平均值等于瞬时值并分离扰动量和忽略二阶微小量，由式(4)和式(5)可得

由式(6)可知:稳态时当 D1=0.5，Uout2=0.5Uin，即实现输出电压平衡，并且电感电流平均值等于两个负载电流之差。

对式(7)进行拉式变换并整理得输出电压uout2对占空比d1的传递函数为

4.2 右桥臂小信号模型

利用同样的方法得，输入输出关系和输出电压uout2对占空比d2(S2占空比)的传递函数。

由式(9)得:稳态时当 D2=0.5，即 Uout2=0.5Uin，实现输出电压平衡，并且电感L2电流平均值也等于两个负载电流之差。

可见，图3所示控制策略是可行的。

图9 控制系统框图Fig．9 Control schematic block

5 仿真分析

按照不平衡负载约为1 500 W左右时电感电流正好进入临界连续模式，参照Buck电路参数设计方法［12］，在输入电压 uin=360 V、开关频率25 kHz时，取电感 L2=L1=230 μH、电容 C1=C2=470 μF。利用仿真软件Saber中器件模型建立该电路和控制电路仿真模型。下面只给出左桥臂电流关系仿真结果，其他情况不再赘述。

5.1 电感L1电流连续

图10(a)给出输入电压uin=360 V、RLoad1=100 Ω、RLoad2=10 Ω时仿真结果。可以看出:电感L1电流脉动量、电容电流等关系满足上述分析:Δ=－= －，Δ= － Δ，i2=+i1等关系。

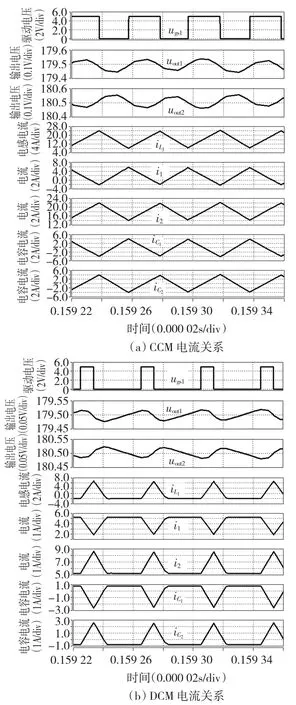
图10 左桥臂主要电流关系仿真图Fig．10 Simulation waves of the current relationships

5.2 电感L1电流断续

图10(b)给出 uin=360 V、RLoad1=40 Ω、RLoad2=30 Ω时仿真结果。看出，在断续模式下非零期间内电流关系与连续时主要电流关系一致。在断续时:PLoad1=1802/40=810 W，PLoad2=1802/30=1 080 W，输入电流iin=(Pout1+Pout2)/uin=5.25 A，i2=i1=iin=5.25 A。由于电流i1大于(180/40=4.5 A)，所以多余电流(i1－=0.75 A=)对电容C1充电，uout1线性上升;电流i2小于(180/30=6 A)，所以不足电流(i2－=－0.75 A=)由电容C2放电提供，uout2线性下降，并且输出电压变化量Δuout2=－Δuout1、电容电流=－。

6 实验结果

为了验证上述分析，研制一台实验样机。其开关频率为 25 kHz，电感 L1=L2=230 μH，电容C1=C2=470 μF，开关管 S1、S2为 SPW47N60C3，二极管D1、D2为DESI60－06A。以中频半桥逆变电源输入360 V为例(均分为180 V)，进行实验验证。

图11(a)给出电感L1电流连续时实验波形，其中=1.8 A=12.0 A，uout1=180.1 V、uout2=180.0 V。图11(b)给出电感L1电流断续模式波形，其中=2.8 A=6.0 A、uout1=180.5 V、uout2=180.3 V。

图11(c)给出电感L2电流连续模式实验波形，其中=12.7 A=2.4 A、uout1=179.6 V、uout2=179.7 V。图11(d)给出电感L2电流断模式实验波形，其中=4.5 A=2.0 A、uout1=180.0 V、uout2=179.8 V。

从图11中可以看出:当负载 RLoad2大于负载RLoad1时，左桥臂工作;反之右桥臂工作。实验波形与前面的分析也是一致的。

表1和表2给出不同输入电压和负载条件下的实验数据，其中电压偏差Δu=uout1－uout2。

在不同的输入电压和负载条件下的电压偏差可以看出，电压不平衡度小于传统交流电网电压不平衡度，能够很好地实现输出电压平衡。

表1 实验数据1Table 1 The experimental data 1

表2 实验数据2Table 2 The experimental data 2

图11 电流连续和断续实验波形Fig．11 Experimental waveforms

7 结语

微型直流电网是一种新型直流输电系统，随着新能源发电技术的发展而得到研究。本文研究了一种新型电压均衡电路和控制策略。它避免桥式拓扑结构中直通的危险，可以在两线微型直流电网改造一根中线，满足了不同用电设备对输入电压的要求。文中详细地分析了电压均衡器工作原理和建立其小信号模型。最后进行原理性仿真和实验验证，仿真和实验结果表明，该电路和控制策略能够实现电压平衡。本文研究内容同样可以应用在串联电容、半桥变换器输入端等需要均压的场合。

［1］AZBE V，MIHALIC R．Distributed generation from renewable sources in an isolated DC network ［J］．Renewable Energy，2006，31(14):2370－2384．

［2］唐任远，张洪阳，张志峰，等．永磁风力发电机分布式直流并网动态电压解耦补偿控制［J］．电机与控制学报，2011，15(5):1－6．

TANG Renyuan，ZHANG Hongyang，ZHANG Zhifeng，et al．Dynamic voltage decoupling compensation control of distributed DC grid converter for permanent magnet wind generator［J］．Eletric Machines and Control，2011，15(5):1 －6．

［3］张先进，陈杰，龚春英．非并网风力发电系统的电压协调控制［J］．电力系统自动化，2008，32(22):91－93．

ZHANG Xianjin，CHEN Jie，GONG Chunying．Coordinated control of voltage in wind power system without gird connection ［J］．Automation of Electric Power System，2008，32(22):91 －93．

［4］KAKIGANO H，MIURA Y，ISE T，et al．DC voltage control of the DC micro-grid for super high quality distribution［C］//Power Electronics Specialists Conference，June 18 － 22，2006，Jeju，Korea．IEEE，2006:518－525．

［5］KAKIGANO H，MIURA Y，ISE T，et al．DC micro-grid for super high quality distribution-system configuration and control of distributed generations and energy storage devices［C］//Power Electronics Specialists Conference，June 18 － 22，2006，Jeju，Korea．2006:1－7．

［6］KAKIGANO H，MIURA Y，ISE T．Low-voltage bipolar-type dc microgrid for super high quality distribution［J］．IEEE Transactions on Power Electronics，2010，25(12):3066 －3075．

［7］LAGO J，MOIA J，HELDWEIN M L．Evaluation of power converters to implement bipolar dc active distribution networks-dc-dc converters［C］//Energy Conversion Congress and Exposition，Sept 17－22，2011，Phoenix，Arizona，USA．2011:985－990．

［8］张先进，龚春英．一种SPWM控制双Buck半桥逆变器研究［J］．电气传动，2009，39(2):48－51．

ZHANG Xianjin，GONG Chunying．Research on dual buck half bridge inverter based on SPWM control［J］．Electric Drive，2009，39(2):48－51．

［9］YAO Zhilei，XIAO Lan，YAN Yangguang．Dual-buck full-bridge inverter with hysteresis current control［J］．IEEE Transactions on Industry Electronics，2009，56(8):3153 －3160．

［10］XIAO Huafeng，XIE Shaojun．Transformerless split-inductor neutral point clamped three-level PV grid-connected inverter［J］．IEEE Transactions on Power Electronics，2012，27(4):1799－1808．

［11］张卫平．开关变换器的建模与控制［M］．北京:中国电力出版社，2006．

［12］丁道宏．电力电子技术［M］．北京:航空工业出版社，1999．