一种改进的掩膜割线相位解缠算法*

钟何平 唐劲松 张 森 张学波

(海军工程大学电子工程学院，武汉 430033)

一种改进的掩膜割线相位解缠算法*

钟何平 唐劲松 张 森 张学波

(海军工程大学电子工程学院，武汉 430033)

为优化掩膜区域的相位解缠结果，提出一种改进的掩膜割线相位解缠算法。掩膜区域生成后，直接对非掩膜区域进行相位求解，然后对低质量相位区域采用“消圈”法来最小化掩膜区域相位的不连续性，达到消除传统掩膜割线算法中的解缠“死区”，并保持相位连续性的目的。对InSAR和InSAS干涉图的解缠结果表明:该方法消除了传统掩膜割线法中的解缠“死区”，提高了解缠相位质量。

InSAR;InSAS;相位解缠;掩膜割线;消圈

1 引言

干涉SAR(InSAR)和干涉SAS(InSAS)都是通过两个信号接收器接收来自同一区域的回波，得到单视复数影像数据，后经成像处理和干涉运算得到干涉图像，进一步反演出目标区域高程信息。由于干涉合成得到的干涉图上点的相位差值丢失了2kπ，发生了相位模糊，而只有将模糊的相位恢复出来，才能反演出目标区域高程信息。这种将相位由主值恢复为真实值的过程称为相位解缠。相位解缠精度是利用干涉技术获取高精度目标高程信息的关键，展开后的相位直接关系到所提取的DEM信息的精度［1，2］。由于 InSAR 和 InSAS的成像结果中会出现透视压缩、阴影和层叠，从而引起两幅图像相干性下降，以及由其他原因引起的去相关现象和在信号处理中引入的相干噪声等，使得InSAR和InSAS数据的相位解缠过程变得十分困难。

目前存在的相位解缠算法主要分为两类:路径跟踪算法［3，4］和最小范数法［5，6］。路径跟踪算法的基本策略是将可能的误差传递限制在噪声区域内，通过选择合适的积分路径，隔绝噪声区，阻止相位误差的全程传递。这类算法通过识别残差点后设置枝切线限制积分路径，或者在质量图引导下，从高质量相位区域开始积分，然后逐步过渡到低质量相位区域。路径跟踪算法特点是在高质量区域求解结果较好，在低质量区域容易出现解缠“死区”，或造成解缠相位的2π倍数跳跃。最小范数算法则是将相位解缠问题转化为最小化全局函数问题，通过寻求一个全局的解缠相位来拟合观测的缠绕相位。最常用的最小范数方法是最小二乘法，即求使展开相位梯度与缠绕相位梯度整体偏差最小的L2范数解［5］。最小范数法解缠结果比较平滑，但不能很好地反映真实的相位梯度，而且计算效率低下。此外，还有Costantini［7］的基于网络流的相位解缠算法，该算法将相位解缠问题转化为求解最小费用流的网络优化问题，降低了相位解缠算法的时间和空间复杂度。

本文针对路径跟踪算法在低质量区域解缠效果差的缺点，提出了一种改进的掩膜割线相位解缠算法。首先根据残差点和相位质量图生成低质量掩膜区域，并直接对未掩膜区域进行积分求解，然后在掩膜区域内部和边缘逐步“消圈”，缩减低质量区域相位的不连续性，达到平滑低质量区域解缠相位的目的。对InSAR和InSAS的解缠试验结果表明:该方法在保持高质量相位区域解缠精度的同时，有效消除了低质量相位区域中的解缠“死区”，优化了相位解缠结果。

2 相位解缠的基本原理

设相位是二维的连续函数，并且从某一个点r0沿某一条路径C到任意一点r的梯度已知，则点r的相位为

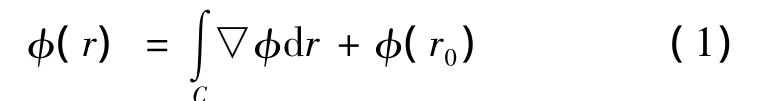
其中，▽φ是真实相位梯度，φ(r0)是起始点相位。但在实际情况下，由于相位噪声、欠采样、层叠和阴影等因素使得绝对相位梯度出现大于π的情况。因此，二维相位解缠在采用式(1)对相位梯度进行积分时存在路径的选择问题，不同的路径积分将会得到不同的解缠结果。

1987年Ghiglia等［8］首先发现了沿不同路径积分解缠结果不一致的现象，这种不一致现象仅发生在一些孤立的点或小的区域，它们可以通过一个2×2的像素模板进行检测，这些孤立的点或小的区域称为残差点。残差点是路径跟踪相位解缠算法一个很重要的指示器，它表征了干涉相位的质量，也为正确的路径设置提供了帮助。Ghiglia和 Pritt［9］首先将复变函数中关于围线积分的留数定理(Residue Theorem)借用到二维相位解缠中构造出一个类似定理，即

式(2)表明二维相位解缠中解缠结果与路径无关的条件为积分路径所围的封闭区域内残差电荷平衡。

3 传统掩膜割线法

掩膜割线法［9］吸收了枝切法和质量引导算法的优点，有效避免了枝切法中枝切线穿越高质量区域的缺点。

掩膜割线法的特点是利用相位质量图来优化枝切线的设置，将生成的枝切线限制在低质量相位区域，防止因枝切线设置不当造成的误差传播。它在检测出残差点后，依靠质量图引导，穿过低质量区域生成像元掩膜，当生成的像元所连接的残差点电荷平衡或像元掩膜到达图像边界时，停止生长。完成掩膜生成后，对其进行细化处理，缩小掩膜区域，然后以剩余掩膜作为枝切线，绕过枝切线求解解缠相位。

传统掩膜割线法掩膜区域生成过程中使用了邻接表来维护相位节点的有序排列。新插入相位节点时，需要进行大量的数据搬移操作以维护相位排列的有序性，效率低下，本文在计算掩膜区域时，采用文献［4］中提出的量化质量引导策略，极大加快了掩膜生成速度。

4 改进的掩膜割线法

改进的掩膜割线法不对初步生成的掩膜区域进行细化处理，而是采用优化策略来求解掩膜区域相位，其具体流程如图1。

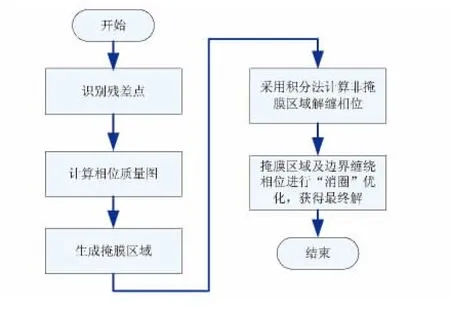
图1 改进掩膜割线法流程Fig.1 Flow chart of the improved mask-cut algorithm

在改进算法中，不需进行掩膜区域细化操作，只需结合非掩膜区域的解缠结果，在掩膜区域缠绕相位及边界解缠相位上进行“消圈”优化，即可获得最终解缠结果。缠绕相位φm，n和解缠相位φm，n之间满足

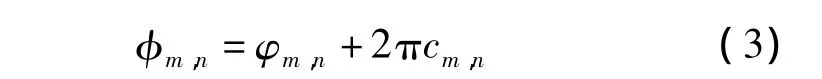
其中，cm，n称为缠绕数。在低质量相位区域内部和已解缠相位边缘，如果一对相邻像素相位值的差在幅度上超过π，则称这两点之间存在不连续。低质量相位区域的求解是以最小化展开相位之间的不连续性为目标［10］，这种不连续性可以采用水平跳跃数vm，n和垂直跳跃数zm，n来度量，分别定义为:

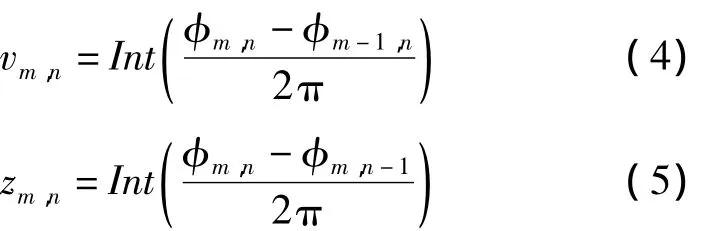
其中Int(·)表示取其最邻近的整数值。因此，低质量相位区域和边界的跳跃数幅度和

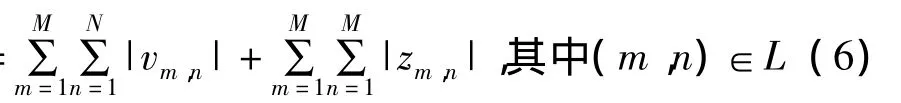
对于目标函数式(6)的求解可以借用最小不连续算法中的“消圈”算法［10］。在最小不连续算法中，跳跃数和缠绕数可以相互推导。缠绕数cm，n的增加将导致跳跃数vm，n、zm，n的增加和vm－1，n、zm，n－1的减小。同理，如果一个区域像元的缠绕数都增加1，则这块区域周围的跳跃数都将增加或减小1。相反，跳跃数的变化也反映缠绕数的变化。

图2中，相位结点用圆圈表示，圆圈内数值表示其相位值，填充斜线的圆圈表示已求解的非掩膜区域相位结点，未填充的圆圈表示掩膜区域的相位结点，小方块表示虚拟的网络结点。边定义为连接一个网络结点及其相邻结点的箭头，表示其分割的一对相位结点的跳跃数。约定向左和向下的箭头表示垂直和水平方向跳跃数的增加，向右和向上的箭头表示跳跃数的减小。从结点(m，n)到结点(m'，n')的边的权值用 δV(m，n，m'，n')表示，跳跃数减小时，δV(m，n，m'，n')=1，跳跃数增加时，δV(m，n，m'，n')=－1。图2中的箭头构成了一个封闭环，箭头旁的数值表示其跳跃数，由于跳跃数都为正值，因此封闭区域的缠绕数是增加的。将正边缘数大于负边缘数的环称为增长环，对于掩膜区域的相位求解，其基本策略就是在掩膜区域及边界寻找增长环进行消圈完成的。完成增长圈消除后，根据优化后相位结点之间的跳跃数计算对应相位结点的缠绕数，即可获得最终的解缠相位。

5 实验结果与分析

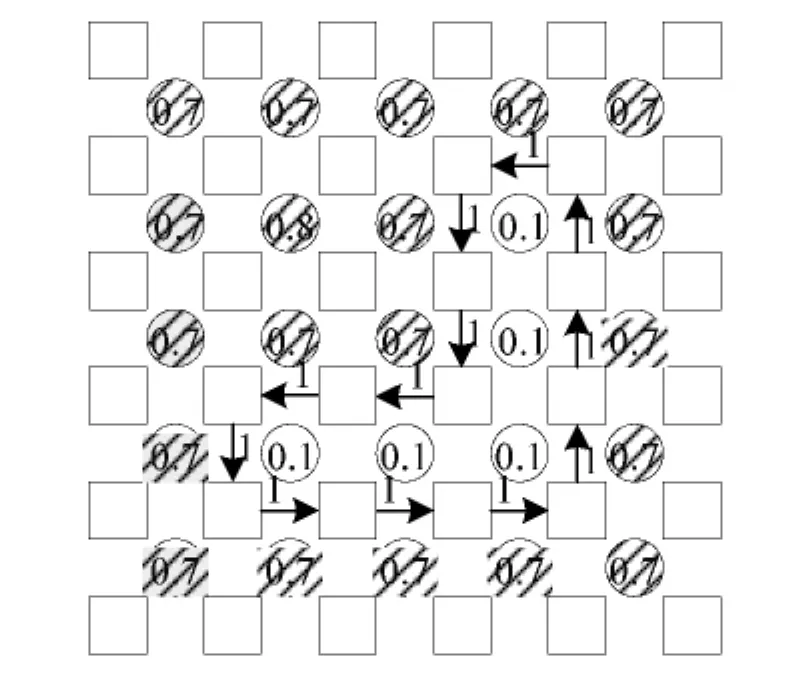
图2 “消圈”示意图Fig.2 Sketch map of“circle cancelling”

为了验证改进掩膜割线相位解缠算法的解缠性能，在如下环境中对不同解缠算法进行比较:CPU:P4 2.6G，内存:2G，Windows XP操作系统，软件VS2005。试验选取两幅干涉数据，一幅为InSAR干涉数据，另一幅为 InSAS干涉数据(图3(a)和4(b))。图3(a)InSAR干涉数据大小为512×512像素，干涉图中间存在大片低质量相位区域。图3(a)对应的相位梯度变化质量图如图3(b)所示，缠绕相位变化剧烈的区域都表征为低质量区域。直接采用枝切法对图3(a)进行解缠，所得结果如图3(c)，在解缠结果中出现了大片解缠“死区”。采用质量引导法对图3(a)进行解缠所得结果如图3(d)所示，从解缠结果中可以看出在低质量区域存在误差传播。根据质量图和量化质量引导策略［4］生成的初始掩膜如图3(e)所示，对图3(e)进行细化操作后，所得结果如图3(f)。从图3(f)中可以看出掩膜区域存在多个孤立区域，造成了最终掩膜割线算法解缠结果图3(g)中的解缠“死区”。采用改进掩膜割线法直接对未掩膜区域进行解缠，所得结果如图3(h)所示。从图3(h)可以看出，不连通的掩膜区域之间存在相位跳变，但在掩膜区域及边界进行“消圈”优化后，所得的最终解缠结果如图3(i)，整个解缠区域不存在解缠“死区”，而且解缠结果平滑，极大优化了解缠结果。

图4(a)是一幅InSAS试验数据原始信号的合成孔径成像结果，该成像区域的最近采样距离为51 m，最远采样距离为231 m，方位向宽度约为60 m，试验参数如表1所示。图4(a)对应的干涉相位如图4(b)，其大小为8 800×1 512像素，从图中可以看出成像区域地形较为平坦，远距离处信号相干性较低，干涉相位质量比较差。传统掩膜割线法的解缠结果如图4(c)所示，其中质量图选用相位梯度变化质量图，从解缠结果中可以看出:除了解缠“死区”外，解缠相位中没有出现明显的相位跳变，但解缠“死区”占有较大比例，严重影响高程数据的生成。改进算法的解缠结果如图4(d)，解缠结果整体上连续，很好地消除了低质量区域的解缠“死区”，优化了解缠结果。

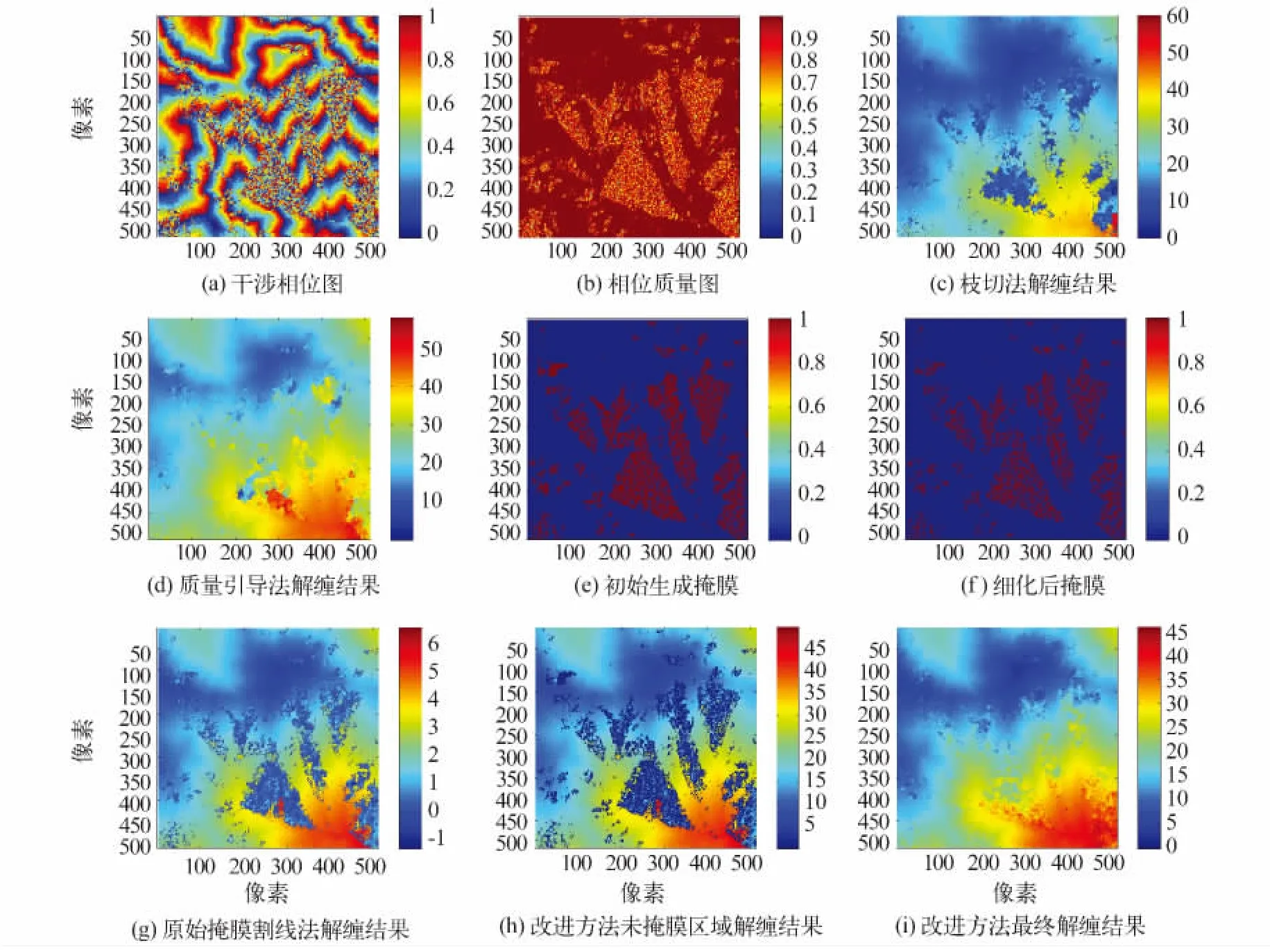
图3 InSAR干涉图解缠试验Fig.3 Unwrapping test on InSAR interferogram

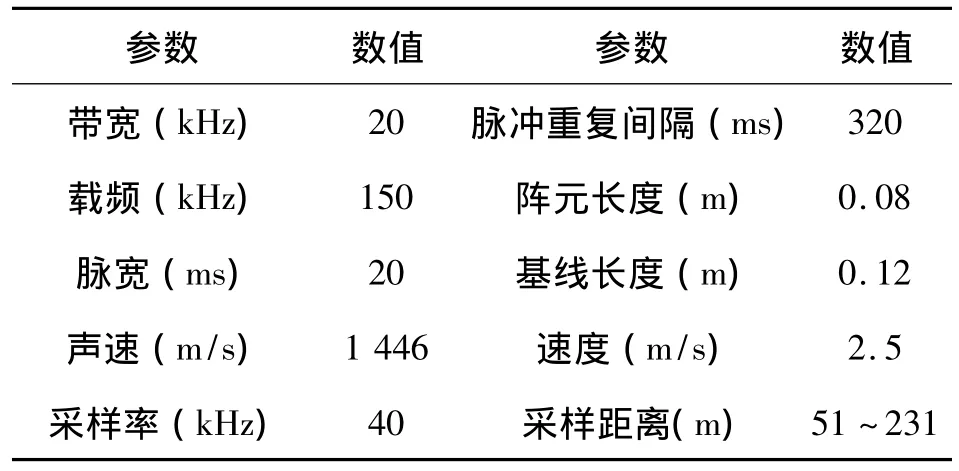
表1 InSAS试验参数Tab.1 Trial parameters of InSAS

此外，我们还从解缠质量和解缠效率两个方面对解缠算法进行了比较分析，结果如表2所示。在传统和改进算法中，掩膜生成都采用了量化质量引导算法［4］，质量等级设为1 000。从表2中可以看出，改进算法比传统算法解缠所需时间稍长，但是不连续性方面改进算法远优于传统算法。对InSAR干涉图解缠时，传统算法需要533 ms，解缠结果中的不连续性长度和大小分别为29 885和58 463，而改进算法所需时间为626 ms，但是解缠结果中的不连续性长度和大小都显著降低，分别为7 954和7 956。对高维数InSAS干涉图解缠，传统算法需要5 126 ms，改进算法需要6 327 ms，但解缠结果中的不连续性长度和大小分别由213 108、1 997 280降低到32 544、33 547，极大优化了解缠结果。

表2 不同算法解缠效率和解缠质量比较Tab.2 Comparison of unwrapped efficiency and unwrapped quality of different algorithms

图4 InSAS干涉图解缠试验Fig.4 Unwrapping test on InSAS interferogram

6 结论

针对传统掩膜割线相位解缠算法容易在低质量相位区域出现解缠“死区”的缺点，提出了一种改进的掩膜割线相位解缠算法。试验结果表明:改进算法在保持高质量相位区域解缠精度的同时，消除了低质量区域的解缠“死区”，优化了解缠结果。

1 李平湘，杨杰.雷达干涉测量原理与应用［M］.北京:测绘出版社，2006.(Li Pingxiang and Yang Jie.Synthetic aperture radar interferometry principle and application［M］.Beijing，Surveying and Mapping Press，2006)

2 王超、张红、刘智.星载合成孔径雷达干涉测量［M］.北京:科学出版社，2002.(Wang Chao，Zhang Hong and Liu Zhi.Spaceborne synthetic aperture radar interferometry［M］.Beijing，Science Press，2002)

3 Zheng Dongliang and Da Feipeng.A novel algorithm for branch cut phase unwrapping［J］.Optics and Lasers in Engineering，2011，49(5):609 －617.

4 Zhong Heping，et al.An improved quality-guided phase-unwrapping algorithm based on priority queue［J］.IEEE Geoscience and Remote Sensing Letters.2011，8(2):364 －368.

5 陈强，等.基于边界探测的InSAR最小二乘整周相位解缠方法［J］.测绘学报，2012，41(3):441 － 448.(Chen Qiang，et al.InSAR phase unwrapping using least squares method with integer ambiguity resolution and edge detection［J］.Cehui Xuebao/Acta Geodaetica et Cartographica Sinica，2012，41(3):441 －448)

6 Flynn T J.Consistent 2-D phase unwrapping guided by a quality map［A］.Proceedings of the 1996 international geoscience and remote sensing symposium［C］.Lincoln，NE，USA，1996:2 057 －2 059.

7 Costantini M.A novel phase unwrapping method based on network programming［J］.IEEE Transactions on Geoscience and Remote Sensing，1998，36(3):813 －21.

8 Ghiglia D C，Mastin G A and Romero L A.Cellular-automata method for phase unwrapping［J］.Journal of the Optical Society of America A(Optics and Image Science)，1987，4(1):267－280.

9 Ghiglia C D and Pritt D M.Two-dimensional phase unwrapping:theory，algorithm，and software［M］.New York:John Wiley ＆ Sons.Inc，1998.

10 Flynn T J.Two-dimensional phase unwrapping with minimum weighted discontinuity［J］.Journal of the Optical Society of America A:Optics and Image Science，and Vision，1997，14(10):2 692 －2 692.

AN IMPROVED MASK-CUT PHASE UNWRAPPING ALGORITHM

Zhong Heping，Tang Jinsong，Zhang Sen and Zhang Xuebo
(College of Electronic Engineering，Naval University of Engineering，Wuhan430033)

In order to optimize the unwrapped result of those mask areas，an improved mask-cut phase unwrapping algorithm is proposed.After the mask generation，those non-mask areas are unwrapped directly，then the“circle cancelling”method is performed during those mask areas to minimize the discontinuity，which can remove those“died area”and keep the unwrapped result continuous.The tests performed on InSAR and InSAS interferograms show that the improved algorithm removes the“died area”of the unwrapped result successfully and greatly enhances its quality.

InSAR;InSAS;phase unwrapping;mask-cut;circle cancelling

P207

A

1671-5942(2013)05-00101-05

2012-12-27

国家自然科学基金(41304015，61072092，61101205)

钟何平，男，1983年生，讲师，研究方向为干涉信号处理.E－mail:zheping525@sohu.com