用绝对重力仪测定超导重力仪格值的精度分析*

陈晓东 孙和平 张为民 郝兴华

(中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉 430077)

用绝对重力仪测定超导重力仪格值的精度分析*

陈晓东 孙和平 张为民 郝兴华

(中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉 430077)

讨论用绝对重力仪观测数据测定超导重力仪格值精度问题，分析影响该精度的各种可能因素。分析说明，选择大潮期间进行格值标定对提高标定精度有利，标定计算前必须去掉仪器的线性漂移，同时还必须检验并改正数据间的时间偏移。以武汉台用FG5-112绝对重力仪对GWR-C032超导重力仪的实测标定结果表明，达到0.1%的相对标定精度是比较困难的，需要非常长的绝对重力观测时间;而达到0.2%的相对标定精度，仅需要5天的绝对重力观测数据，且可满足大多数超导重力仪观测精度的需求。

FG5绝对重力仪;GWR超导重力仪;格值;仪器漂移;时间偏移

1 引言

用仪器同址观测比对的方法获得重力仪的格值是一种常用重力仪标定方法，广泛应用于实际重力仪的格值测定之中［1－5］。格值标定的相对精度要求在0.1%的量级，主要是因为超导重力仪振幅因子估算的精度和目前潮汐模型中潮汐参数的相对精度都为0.1%的量级或更高［4］。仪器同址观测比对的方法基于以下假设:在相距很近的两测点上的重力场变化相同，两台仪器观测的是同一物理量，观测值相等，即如果已知其中一台重力仪的格值，就可以估算另一台重力仪的格值。

目前在观测地球重力场的各类仪器之中，超导重力仪的观测精度最高，其分辨率在10－11ms－2量级，观测精度在 10－10ms－2的量级［8－10］。在利用FG5绝对重力仪测定超导重力仪格值时，许多研究人员会有这样两个问题:用低精度重力仪能不能测定较高精度重力仪的格值?测定格值的精度与两台重力仪各自的精度的关系如何?本文就这两个问题利用实测数据进行了探讨。对于第一个问题，答案是肯定的。对于第二个问题，实际上在获得了两台重力仪在同一点的重力观测数据之后，格值测定的问题就转化为如何利用观测数据进行估算格值，而求解问题的最终方法是线性最小二乘回归方法，问题就转化为格值的精度估算问题。测定格值的精度与两台仪器各自的精度的关系可以基于线性最小二乘回归模型和误差传播定律来推导得到。

本文基于线性最小二乘回归模型和误差传播定律，利用FG5绝对重力仪和GWR超导重力仪2011年在武汉台的同址观测数据，研究了测定超导重力仪格值时的精度估算问题，分析了影响格值测定的各种影响因素，证实了用FG5绝对重力仪测定超导重力仪格值的可行性。

2 线性最小二乘回归数学原理

因为两台重力仪观测的为同一物理场，如果仪器为线性响应，则两列观测数据亦呈线性关系。计算模型为:

式中，Y为FG5绝对重力仪的观测值，X为GWR超导重力仪的观测值，a为回归截距项，b为回归斜率，此处b就是我们最终要计算的格值。如果分别对X和Y进行了n次独立观测，得到n对观测值(Yi，Xi)，i=1，2，…，n，则有:

对式(3)两边分别平方求和得，

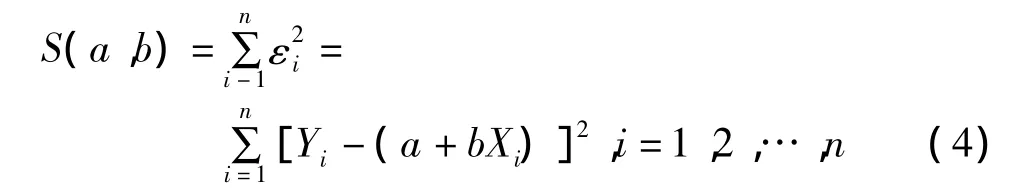
当S(a，b)取到极小值时，则S(a，b)对于a和b的一阶偏导数等于零，得:

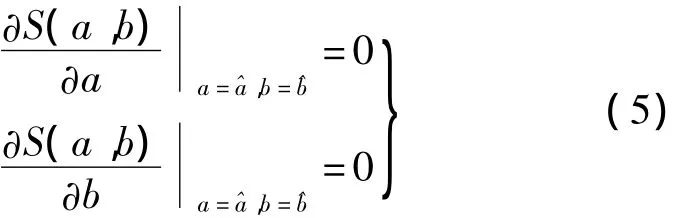
由式(4)和(5)得a和b的估计量和为:

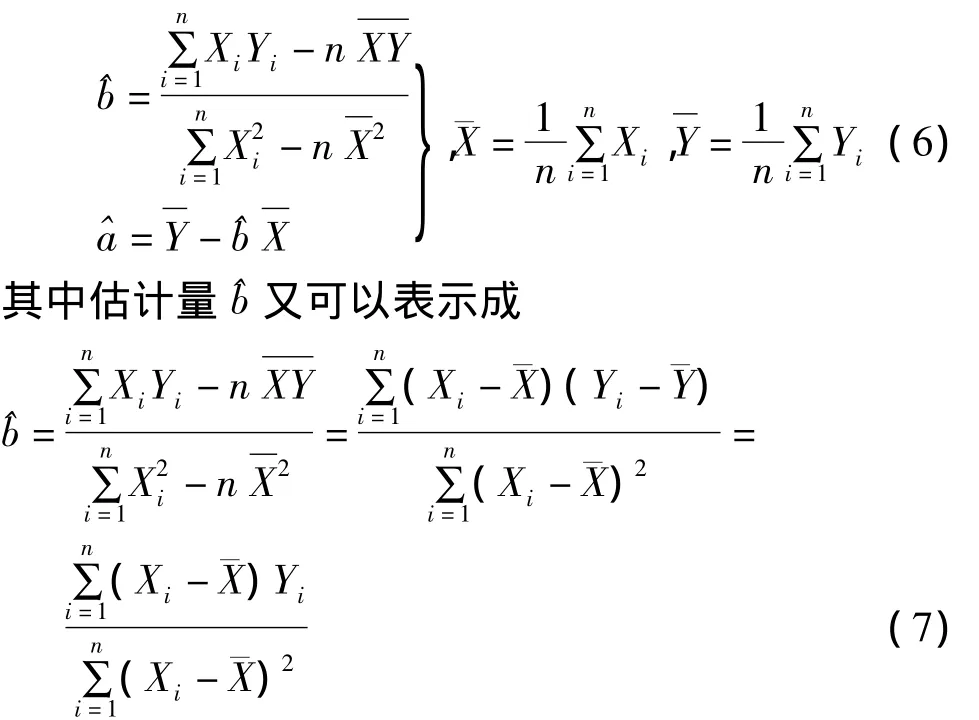
3 用误差协方差传播律推导格值精度

估计量和的误差来源于观测数据Xi和Yi的误差。在估计和的精度时，因为观测值Xi比Yi要高2个数量级，为简单起见，我们可以假定所有观测的偏差都是由于因变量Yi引起的，因为GWR超导重力仪的精度比FG5绝对重力仪的精度高得多，所以这样的假设是合理的。为了便于说明问题，将假定的观测值分别记为X'i和Y'i，X'i的中误差 δX'为零，Y'i的中误差(仍约为10－8ms－2)。利用误差协方差传播律估计和的精度时，公式(7)中所有Xi都是真值没有误差。所以根据误差传播定律，由式(7)中的最后一项，得到的中误差δ的平方为:

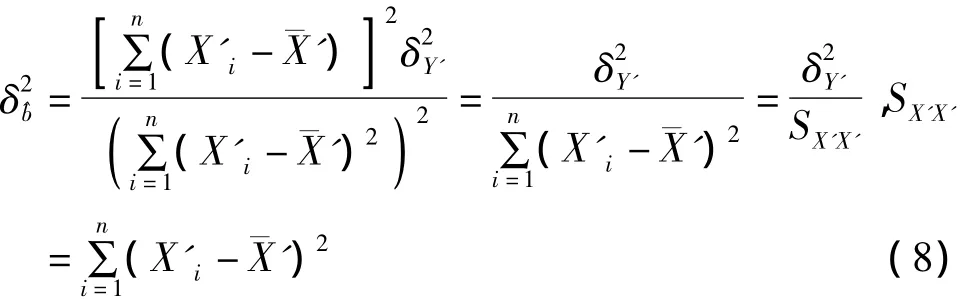
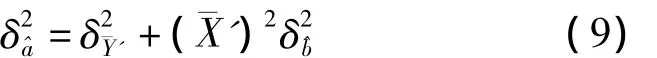
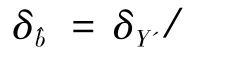
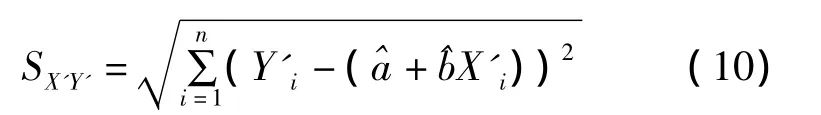
当回归方程是由观测数据拟合出来时，则SX'Y'提供了关于δY'的具有n－2个自由度的估计。

当用残差均方差SX'Y'替代δY'时，两台仪器的观测值X'i和Y'i中不是由于重力场变化引起的观测值变化会影响的估算，可能的因素有仪器的漂移、时间偏移、线性量程的范围等。仪器漂移的不同对估算的影响是显然的，因为两台仪器的漂移不可能还适用式(1)给出的模型，所以在计算格值前必须要去掉漂移的影响。仪器的时间偏移使得两套仪器的观测时间序列不对应，这对于估算的影响也是显而易见的，通常将其中的一个数据序列前后移动一个或几个采样间隔使得观测曲线的峰值和谷值对应即可去掉时间偏移的影响。仪器线性量程的范围使得只有在线性量程范围之内的观测值才适用式(1)给出的模型，超出线性量程范围的观测值对于的估算显然也是不利的。

4 用FG5-112绝对重力仪测定GWRC032超导重力仪的格值

4.1 观测方案的制定

按照分析，观测在大潮期间对于提高测定精度有利，因此在观测之前需要进行重力潮汐预报值的计算。我们用武汉台超导重力仪的观测潮汐参数事先计算了2011年2月15日—3月31日的重力潮汐预报值(图1)。实际观测时间从2011年3月3日12时0分10秒开始到3月7日1时19分50秒结束(图1中两条粗黑实线之间)，刚好在大潮期间。考虑到FG5-112绝对重力仪每一个落体对仪器都有损害，不能连续地长时间观测，FG5-112绝对重力仪的观测方案如下:每10秒钟一个观测值，观测20分钟，停测10分钟，观测5天。

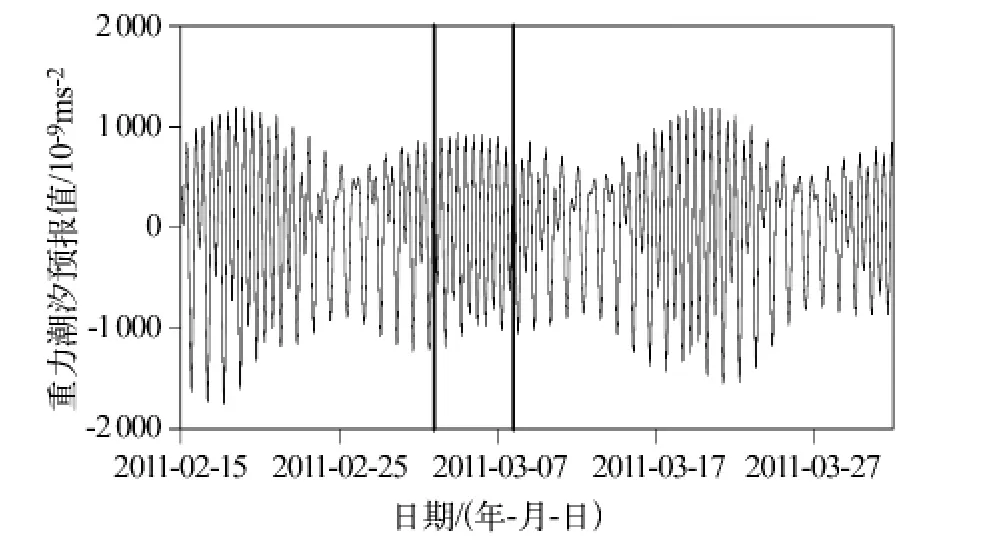
图1 预报重力潮汐和标定工作实际观测时间段Fig.1 Predicted gravity tides and observing time period of the calibration work

关于观测时间天数的确定，参考以前的观测经验［1－3］，观测天数不能太少也不能太多，考虑到实测数据中的异常观测数据，5天的连续观测比较合适。

4.2 观测数据中仪器线性漂移、时间偏移、长期漂移的检验

FG5-112绝对重力仪的观测数据如图2中的十字曲线所示，对应的GWR-C032超导重力仪的观测数据如图2中实曲线所示，为了与绝对重力仪的观测数据相比较，超导重力仪的观测数据已乘以－1，绝对重力仪已经减去了一个常数，并且两个数据都只画出在纵坐标轴刻度范围内的观测值。FG5绝对重力仪观测时间共计3天13时19分40秒，共记录10 320个观测值。

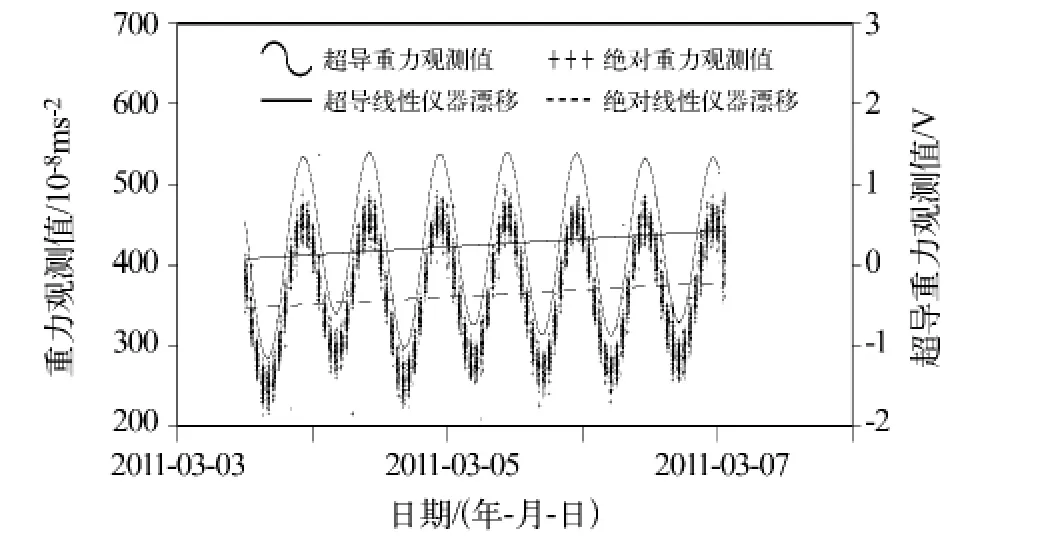
图2 FG5-112绝对重力仪和GWR-C032超导重力仪观测值及其各自线性仪器漂移Fig.2 Observed data of the FG5-112 absolute gravimeter and the GWR-C032 superconducting gravimeter，and their linear instrumental drifts respectively

仪器长期漂移的检验通常只检验线性仪器漂移，主要原因是在观测时间段内两种类型的重力仪的仪器漂移都非常小，可以近似为线性变化。对观测数据进行线性拟合，看拟合直线的斜率的大小。如图2中所示，FG5-112绝对重力仪的线性漂移为虚直线，其斜率约为 0.000 1 ×10－8ms－2，5 天的漂移约有 4.32 ×10－8ms－2;GWR-C032 超导重力仪的线性漂移为实直线，其斜率约为0.000 001 15V，5天的漂移约有0.05V。在进行格值计算之前，仪器漂移必须去掉，并且还要注意异常数据对漂移的影响。

检验时间偏移的方法是图形法，因为一般情况下绝对重力观测前都要与超导重力仪的时间系统校对，但是还是有仪器中各种电路的响应时间差。有两种作图形式可以看时间差:1)如图3将两个时间序列的横轴为时间，将两台仪器的观测数据时间序列作在同一个图形中作比较，如果有时间偏移，则峰值和谷值不会完美对应;2)如图4以两个时间序列的数据分别作为横轴和纵轴，看两个时间序列的线性关系，如果是完全线性的，则无时间偏移;如果线性关系呈椭圆形，则存在时间偏移(如图3将超导重力仪观测值前移10分钟后，两观测值呈椭圆形状)。通常两种图形一起来检验是否有时间偏移。如果存在时间偏移，需要移动其中的一个观测序列，一般移动采样率高的时间序列，必要的时候，还可以对数据进行插值。从图2中可以看出，绝对和超导重力仪观测值在时间序列中峰值和谷值完全对应，看不出时间偏移;从图4中也可以看出，两个时间序列呈完全线性关系，看不出有丝毫的椭圆形，所以本次标定中无明显的时间偏移。

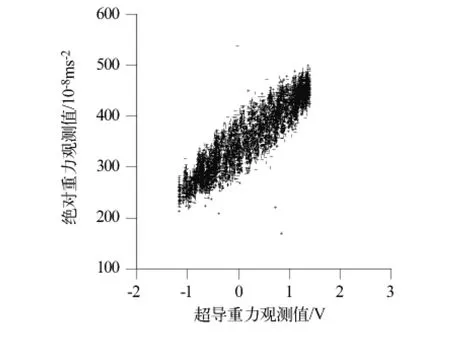
图3 绝对和超导重力观测值的线性关系(超导观测值前移10分钟后)Fig.3 Linear relationship of the observations of the absolute and superconducting gravimeters(the data from the superconducting gravimeter are shifted 10 minutes ahead)

4.3 标定计算结果与分析

在去掉线性漂移后，我们采用线性迭代回归对图4中所示的FG5-112绝对重力仪和GWR-C032超导重力仪观测数据进行回归计算，回归残差的均方差作为中误差，以三倍中误差作为剔除异常观测的限差，每次迭代中都去掉了两台重力仪各自的仪器漂移，当格值因子的变化小于0.001时停止迭代。实际计算中迭代5次后计算终止，此时参与格值计算的绝对和超导重力仪观测值如图5所示，共9 859对观测值，绝对重力仪的数据利用率为用率约为95%。计算得到的格值为(－84.557 4±0.158 4)×10－8ms－2/V，相对标定精度为0.19%。从图5 可以看出，通过迭代，异常观测值得到了剔除，非常好地保留了有效观测值，说明迭代计算的有效性。

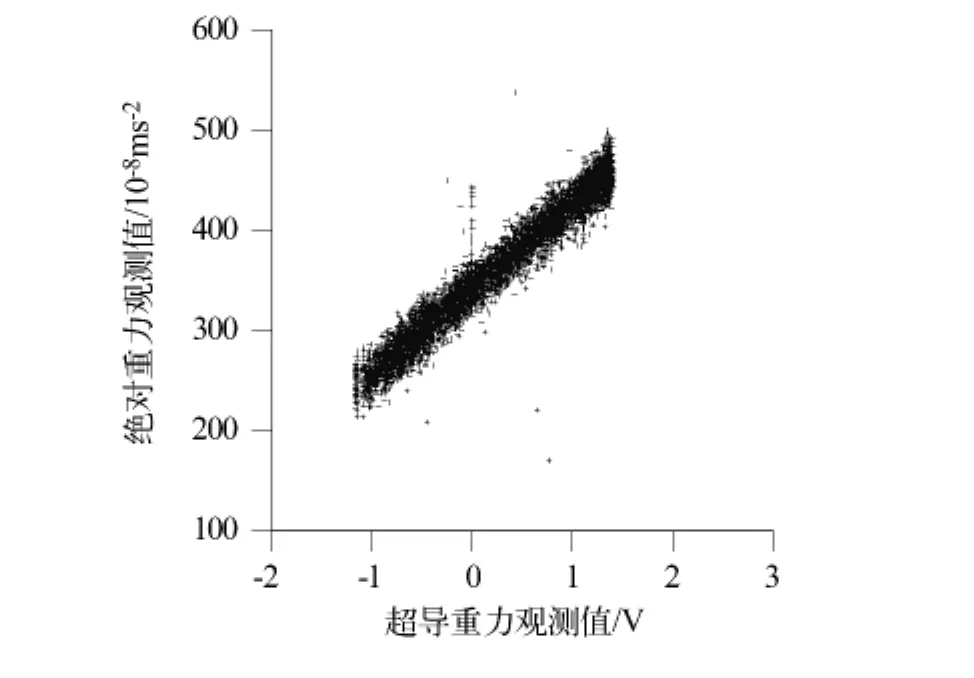
图4 绝对和超导重力观测值的线性关系Fig.4 Linear relationship of the observations of the absolute and superconducting gravimeters

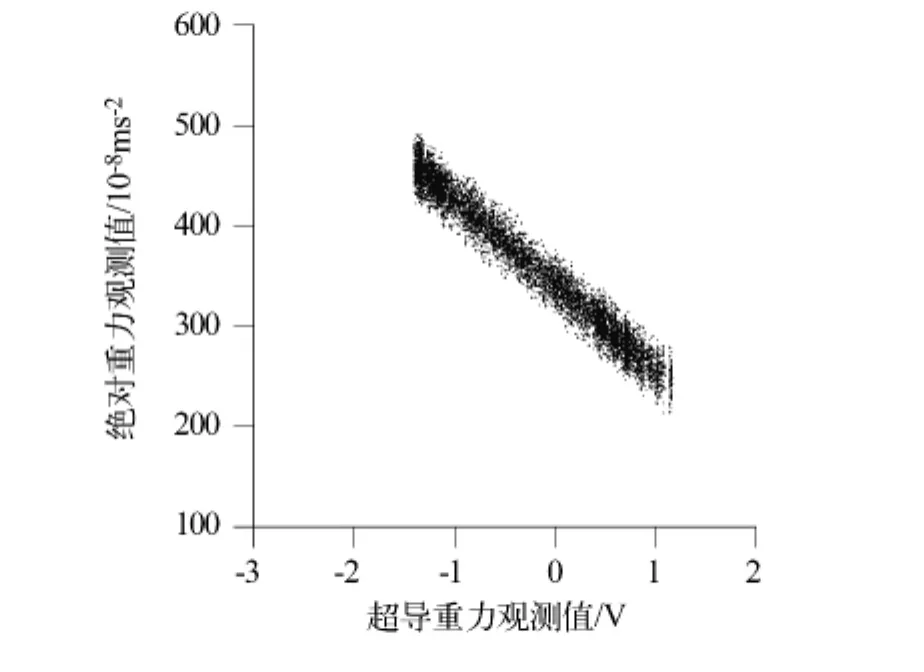
图5 绝对和超导重力观测值的线性关系Fig.5 Linear relationship of the observations of the absolute and superconducting gravimeters

利用得到的参与计算格值的9 859个数据，探讨观测值的个数与格值计算精度间的关系。以100个数据对为每次增加的参与计算格值的数据，首次计算使用100个数据对。图6给出了格值及其估算精度随数据对个数的变化，格值及其精度都是从第1 000个数据对开始作图的，前面100～900个数据对的结果格值及其精度变化太大，显然与最终的计算结果相差太远，不予考虑。从图6可以看出，随着计算数据对个数的增加，格值迅速稳定到最终测定的格值附近，其精度也迅速减小，随着观测个数对的增加，估算精度越来越高。从第2 000个观测对到第9 000个观测对，对应的观测时间约从1天到4.5天，格值精度约从 0.4 ×10－8ms－2/V 提高到 0.2 ×10－8ms－2/V，并且观测对数量的增加对于格值的相对精度的提高越来越小，要达到0.1%的相对精度，参考上面的最终格值，约为 0.08 ×10－8ms－2/V，需要较长时间的绝对重力观测，对绝对重力仪的损害较大。另外，从图6还可以看出，在有效观测对数从100达到5 600个时，格值为减小的趋势，到达5 600个观测对以后，格值在不断发生微小变化，变化似乎有周期性，与此同时格值的精度却不断提高。这说明还有其他的未知因素在影响格值趋于稳定。

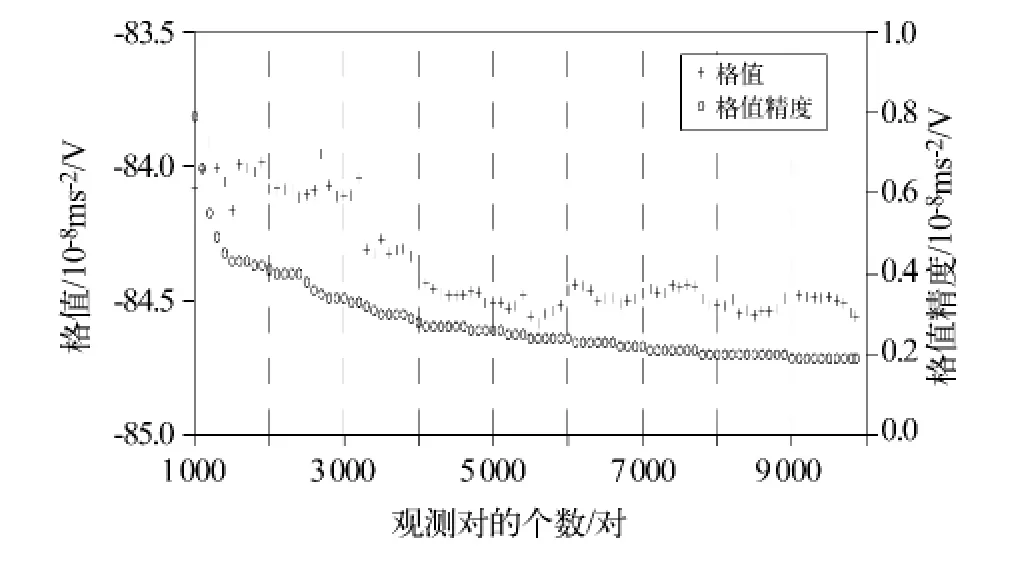
图6 格值及其精度与观测对个数的关系Fig.6 Relationship between the calibration factor，its accuracy and the number of pairs of data

另外，对于相对重力仪格值的相对标定精度，不需要非要达到0.1%相对标定精度。解释如下:重力潮汐的变化幅度在 350 ×10－8ms－2以内，格值0.2%的变化最大可引起重力潮汐总的变化为0.7×10－8ms－2。由于地球背景噪声的影响，大多数超导重力仪的残差标准差大约在0.5×10－8ms－2，许多其他类型的相对重力仪远大于 0.7×10－8ms－2，所以0.2%的标定精度基本满足大多数相对重力仪(包括超导重力仪)的标定需要。因此在用绝对重力仪对其他相对重力仪(包括超导重力仪)进行格值测定时，建议5天的连续观测使标定精度达到0.2%时即可。

5 结论

利用武汉地震台FG5-112绝对重力仪测定GWR-C032超导重力仪格值的实验表明，要达到0.1%的标定精度需要较长的观测时间，对绝对重力仪的损害较大，费时费钱，不实用。建议5天的连续观测使相对标定精度达到0.2%时即可，0.2%的标定精度基本满足相对重力仪(包括超导重力仪)观测数据标定的需要。

1 Sun H P，et al，Accurate determination of calibration factor for tidal gravity observation of a GWR-superconducting gravimeter［J］.Acta Seismologica Sinica，2001，14(6):692－700.

2 Hwang C，et al，Results from parallel superconducting and absolute gravimetric observations and GPS at the Hsinchu(HS)station of GGP，Taiwan［J］.J Geophys R.，(solid earth)， 2009， 114， B07406， Doi:10. 1029/2008JB006195.

3 邢乐林，等.利用绝对重力测量精密测定超导重力仪的格值因子［J］.大地测量与地球动力学，2010，(1):48－50.(Xing Lelin，et al，Scale factor calibration of a superconducting gravimeter by using absolute gravimetry［J］.Journal of Geodesy and Geodynamics，2010，(1):48 －50)

4 Riccardi U，et al.On the accuracy of the calibration of superconducting gravimeters using absolute and spring sensors:a critical comparison［J］.Pure Appl Geophys.，2011，doi:10.1007/s00024－011－0398－8.

5 Meurers B.Superconducting gravimeter calibration by co-located gravity observations:results from GWRC025［J］.Inter J Geophys.，2012，article ID 954271，doi:10.1155/2012/954271.

6 王勇，张为民.FG5绝对重力仪［J］.地壳形变与地震，1996，16(2):94 －97.(Wang Yong and Zhang Weimin，FG5 absolute gravimeter［J］.Crustal Deformation and Earthquake，1996，6(2):94 －97)

7 张为民，等.中国地壳运动观测网络基准站绝对重力的测定［J］.地壳形变与地震，2001，21(4):114－116.(Zhang Weimin，et al，Observation of the absolute gravity for the benchmark stations of the Crustal Movement observation Network of China［J］.Crustal Deformation and Earthquake，2001，(4):114－116)

8 孙和平，等.我国GWR超导重力仪观测资料应用研究进展［J］.大地测量与地球动力学，2002，(4):106－111.(Sun Heping，et al，Progress in application study of gravity observations recorded with a GWR superconducting gravimeter in China［J］.Journal of Geodesy and Geodynamics，2002，(4):106－111)

ACCURACY ANALYSIS ON DETERMINATION OF CALIBRATION FACTOR OF A SUPERCONDUCTING GRAVIMETER USING AN ABSOLUTE GRAVIMETER

Chen Xiaodong，Sun Heping，Zhang Weimin and Hao Xinghua
(State Key Laboratory of Geodesy and Earth’s Dynamics，Institute of Geodesy and Geophysics，CAS，Wuhan430077)

The accuracy estimation of the determination of the calibration factor of a superconducting gravimeter using an absolute gravimeter is discussed in detail.Possible factors affecting the accuracy are analyzed.The result indicates that it can minimize the accuracy to choose the observation period as the large tide period.The linear instrumental drift must be deducted before calculation，and the time shift must be checked and corrected.As an example，the calibration experiment at Wuhan station using an absolute FG5-112 gravimeter to calibrate the GWRC032 superconducting gravimeter shows that it is comparatively difficult to achieve a relative calibration accuracy of 0.1%，which need very long time absolute gravity data.However，a relative calibration accuracy of 0.2%can meet the requirements to calibrate most of the superconducting gravimeters，and this accuracy can be reached using about 5 days absolute gravity data.

FG5 absolute gravimeter;GWR superconducting gravimeter;calibration factor;instrumental drift;time shift

P207

A

1671-5942(2013)05-0145-05

2013-02-18

国家自然科学基金(41021003，40904019，41074053，41004009);大地测量与地球动力学国家实验室基金(L10-09)

陈晓东:男，1975年生，博士，副研究员，主要研究方向为地球重力场、重力潮汐理论研究和观测数据处理、重力仪的标定、重力潮汐数据应用.E －mail:chenxd@whigg.ac.cn