基于北斗双频数据的周跳探测及修复算法*

吴丰波 张书毕 张秋昭 侯晓真

(中国矿业大学环境与测绘学院，徐州 221116)

基于北斗双频数据的周跳探测及修复算法*

吴丰波 张书毕 张秋昭 侯晓真

(中国矿业大学环境与测绘学院，徐州 221116)

针对北斗导航卫星的钟差大、信号噪声大等特点，提出一种周跳探测与修复方法。首先根据单频码相组合，分别确定两个频率上周跳的搜索范围，然后加入载波相位变化率，基于双频载波相位进行最小二乘多项式拟合，拟合结果综合运用Blewitt方法检验标定周跳并剔除野值。根据周跳的整数特性，利用残差最小修复周跳。利用COMPASS-MEO卫星实测数据进行试验，验证了该算法可以有效地检测出所有周跳并快速修复。

北斗导航卫星;周跳探测;单频码相组合法;电离层残差法;Blewitt检验

1 引言

随着我国北斗二代卫星导航系统的建成并投入使用，北斗卫星在国家安全及社会生活各个方面将扮演着越来越重要的角色，研究合理的周跳探测方法以保证后续定位的精度是北斗卫星导航系统的一个重要问题。接收机在载波相位观测中，由于障碍物的阻挡或无线电干扰等原因引起卫星信号短时间失锁，会导致接收机整周计数的突变［1］。目前GPS卫星周跳探测与修复的方法主要包括高次差法、多项式拟合法、电离层残差法、伪距相位组合法、多普勒积分法、拟准检定法、Kalman滤波法和小波变换法等［2－7］。高次差法探测周跳主要受钟差、电离层延迟变化和相位观测噪声的影响;伪距相位组合法受伪距观测噪声的影响大，探测与修复周跳精度不够理想;电离层残差法消除了钟差的影响，探测误差主要由电离层延迟变化决定的，存在探测盲点。多项式拟合法是一种常用的周跳修复方法，根据拟合方法选取适当的周跳阈值条件以及周跳确认准则仍然没有统一的标准。

目前研究的热点是三频数据的周跳探测方法［8］，但市场上大部分北斗接收机只能接受双频数据，综合考虑北斗卫星钟差大、伪距噪声大等因素，本文以双频载波相位观测值组合理论为基础，结合单频码相组合和载波相位变化率，提出一种周跳探测及修复的组合算法。对某厂商接收机实测GPS和北斗数据进行周跳探测与修复对比，验证了该算法对北斗卫星数据的周跳探测及修复的有效性。

2 GPS和北斗卫星周跳探测方法对比

图1所示为某厂商北斗和GPS双系统接收机实测数据，取无周跳的300个历元作双频码相组合周跳探测的对比。在消除接收机钟差、卫星钟差、对流层折射和电离层折射影响后，GPS周跳探测效果明显优于北斗。

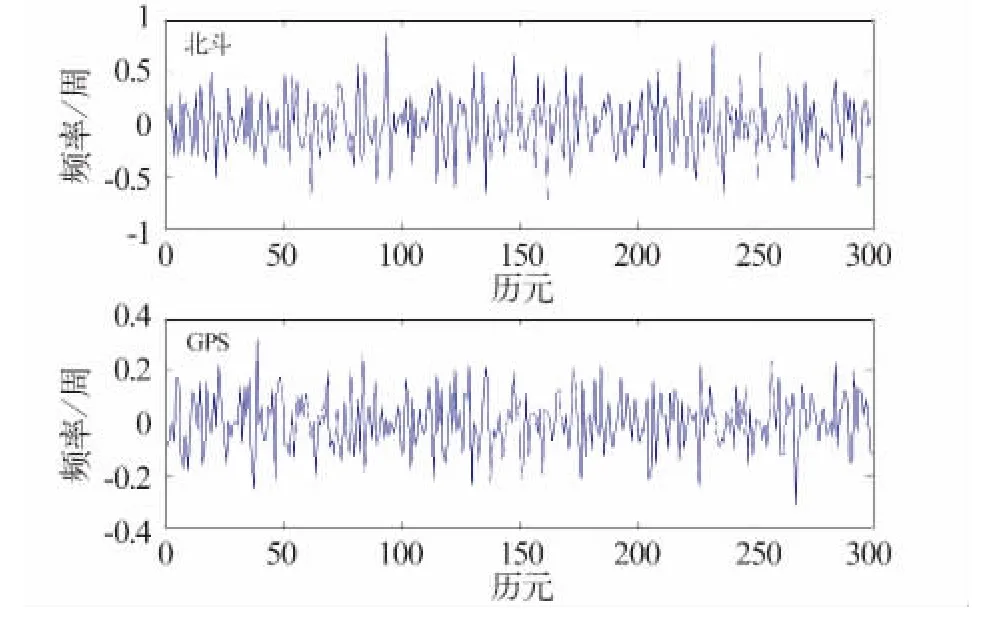
图1 北斗、GPS双频码相组合周跳探测对比Fig.1 Comparison of dual-frequency code between COMPASS and GPS

分别选取高度角较大的GPS和北斗卫星，运用星间做差消除影响较大的接收机误差后再进行高次差，对差分结果影响最大的就是卫星钟差。图2为三次差结果，可以看出图1北斗的卫星钟误差对周跳探测的影响要大于GPS，这也说明北斗卫星钟差大于GPS。

因此，北斗周跳探测方法的选取要尽量减小或消除这些方面的影响，才能更加有效地探测并修复周跳。

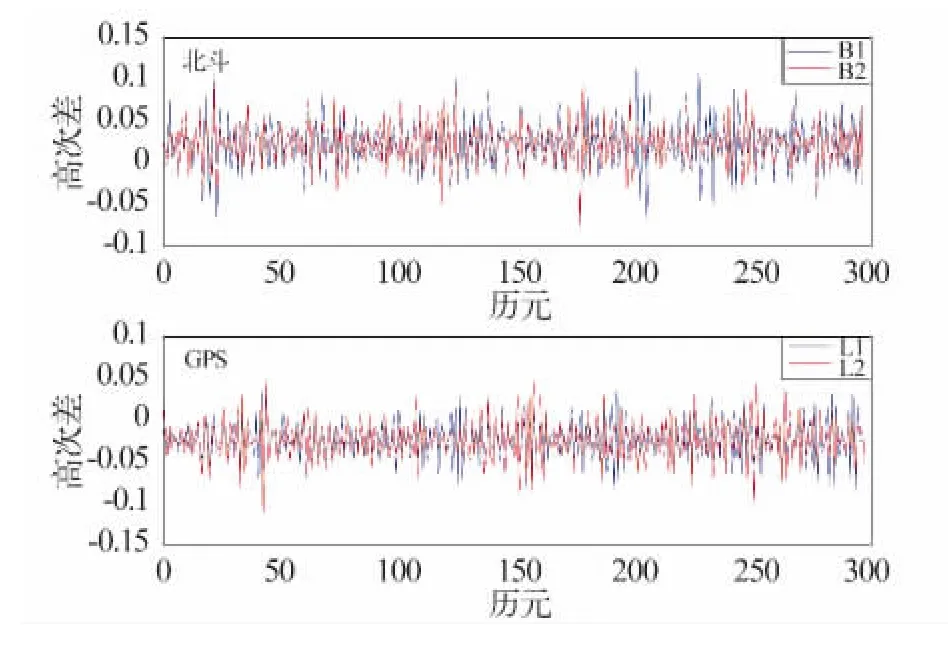
图2 北斗、GPS高次差对比Fig.2 Comparison of higher difference between COMPASS and GPS

3 组合法周跳探测及修复

3.1 观测方程

接收机k对卫星j的码伪距和载波相位的观测方程分别为:

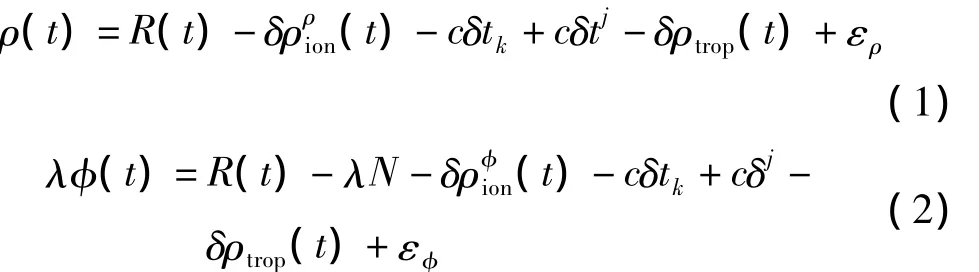
3.2 单频码相组合约束周跳

在码伪距和相位观测值之间取差得:

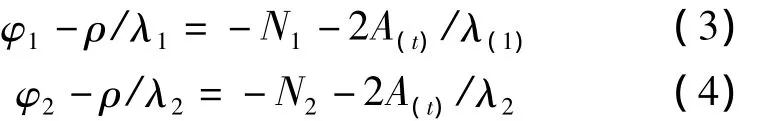
当接收机处于静止或低速运动状态下，电离层活动并不剧烈，该差值不会随时间发生大的变化［5］，因此可逐历元计算该值，判断周跳。北斗导航卫星的观测数据伪距噪声比较大，而该方法只能探测出大周跳，因此仅使用该方法并不能探测出所有周跳。

3.3 基于双频载波相位的多项式拟合

在同一历元之间的双频载波相位观测值之间作差得:

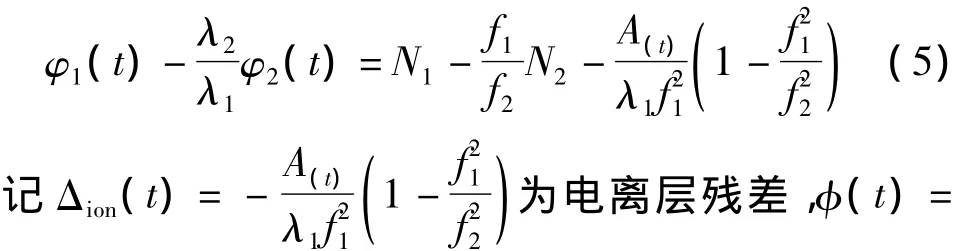
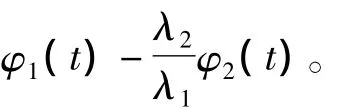
通过式(5)，消除了接收机钟差、卫星钟差和站星几何距离的影响，得到的φ仅包含频率间的模糊度互差、电离层残差和未建模的噪声影响。在没有周跳的情况下，φ的变化主要由电离层残差和噪声波动决定，一般说来，电离层残差变化很缓慢，噪声相对于周跳要小很多，可以通过后续判断滤除［9］。

低动态载波相位观测历元之间相关性较大，一般三阶多项式拟合就能达到很高精度［9］，周跳前双差载波相位观测值符合:

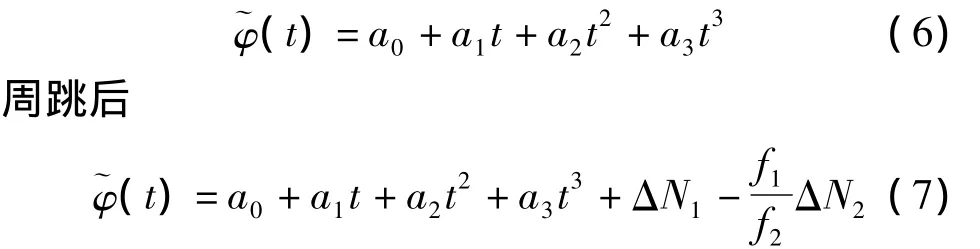
载波相位变化率是载波相位的一阶导数，双差载波相位变化率可写为:

连续的历元之间载波相位变化率主要和接收机的运动状态以及采样间隔相关，当采样间隔较小，接收机低速运动时，历元之间载波相位变化缓慢［9］。而对于消除了接收机和卫星钟差的双频载波相位差，其变化就更趋缓慢，因此，可以考虑取某历元的双频载波相位差的平均值为该历元结束时刻的双频载波相位差变化率。公式表示为:

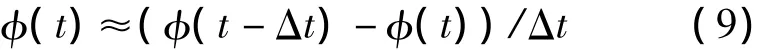
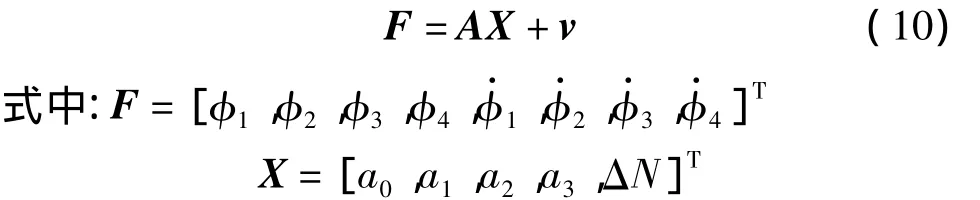
根据最小二乘原理可解得:

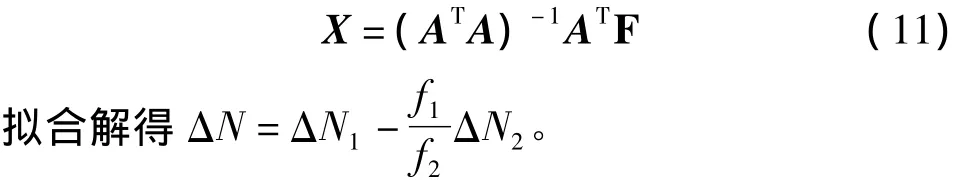
3.4 组合法周跳探测及修复

多项式拟合得到的ΔN是B1、B2周跳的线性组合，对于使 ΔN接近于零的 ΔN1、ΔN2组合很难探测，通过单频码相组合将B1、B2频率上的周跳约束在较小的范围内，再来判断搜索就很容易探测并修复周跳。

根据ΔN判断是否存在周跳，GPS一般采用相位观测噪声的简化模型，即取相位观测中误差为0.01周，利用误差传播定律判断是否存在周跳，而北斗观测噪声比较大，这种方法不具有随机噪声的统计特性，因而会有更多的探测盲点，引入Blewitt探测法［10］用于检定可以有效地解决这个问题。

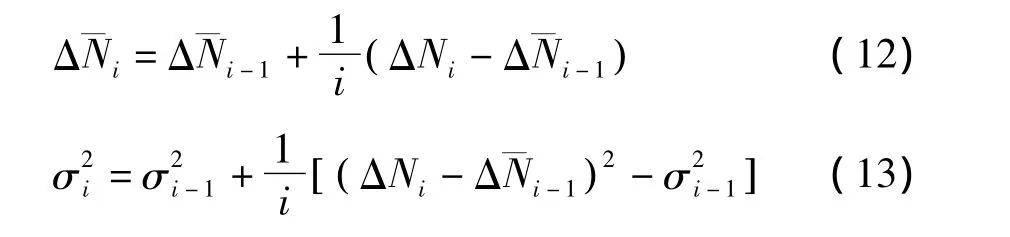
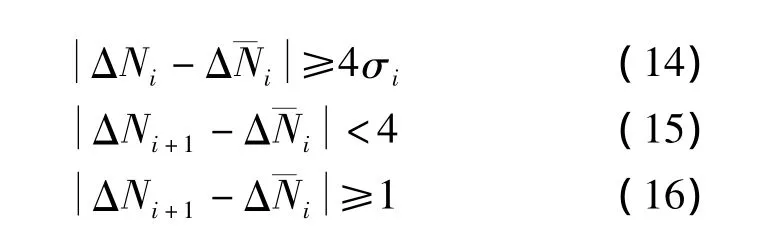
当式(14)和(15)同时成立时，则认为历元i－1和i之间有周跳;当式(14)和(16)同时成立时，则认为历元i为野值［4，7，10］。该方法在有效地探测北斗周跳的同时，还能探测出野值点。

根据周跳的整周特性，利用单频码相组合法可以缩小B1、B2频率上周跳搜索范围，确定周跳搜索阈值。小于搜索阈值的周跳直接搜索，而大于搜索阈值的周跳，则在最接近的周跳整值上下搜索阈值以内搜索。

搜索满足式(17)和(18)的Δ^N1、Δ^N2即为B1、B2上的周跳值。实例分析表明，该方法简单有效，可以准确地分离出周跳。

在北斗伪距噪声的影响下，单频码相组合只能探测出大周跳，基于双频载波相位的多项式拟合探测不出特定的组合周跳。将两种方法结合起来，可以有效的探测所有周跳，组合算法流程图如图3所示。

4 实例分析

试验数据为2012年9月19日在中国矿业大学环测学院实测的一组静态数据，数据采样间隔为1 s，观测到的北斗卫星共6颗，观测数据类型包括L1、L2、C1、P2。

图3 组合算法流程Fig.3 Flow chart of combined algorithm

为更好地验证算法的有效性，选取无周跳的300个历元，人为地在第50历元处加周跳(1，0)，历元100处加周跳(0，1)，历元120处加周跳(1，1)，历元150处加周跳(4，3)，历元200处加周跳(9，7)，历元250处加周跳(76，59)，历元280加连续周跳(0，1)和(1，0)。图4为所测数据单频码相组合周跳示意图，所取300个历元内北斗两个频率上的周跳都约束在5周以内，周跳搜索阈值定为5周。

图4 无周跳的单频码相组合Fig.4 Single-frequency and code without cycle slip

加周跳单频码相组合探测周跳如图5所示，在历元50、100、120、150、280、281 加入的小周跳探测结果仍在五周以内;在历元200加入的周跳基本可以约束到(9，7)。探测并修复历元250的周跳和历元200基本一样。大于5周的周跳能成功探测出来。为清晰说明小周跳的探测及修复，选取其中的一颗卫星进行试验。

基于双频载波相位的多项式拟合周跳如图6所示，可以看出，该方法对于历元50、100、280处的小周跳特别敏感，可以确定有周跳发生;在历元120、150、250、281处也存在较大波动，说明有周跳发生;在历元200的组合周跳(9，7)，探测结果几乎为绝对盲点，结合图5探测结果可以确定有周跳发生。不难发现，单频码相组合法与基于双频载波相位的多项式拟合在探测周跳方面能够优势互补，提高了周跳探测的成功率。

周跳修复采用类似整周模糊度的搜索算法，周跳的正确与否根据式(17)残差最小和式(18)进行判断，表1为根据标记的小周跳和大周跳历元进行搜索，得到的残差最小的两个结果，其中历元280、281分别和50、120的搜索结果一样，结果表明本文设置的具有代表性的周跳修复成功率100%。

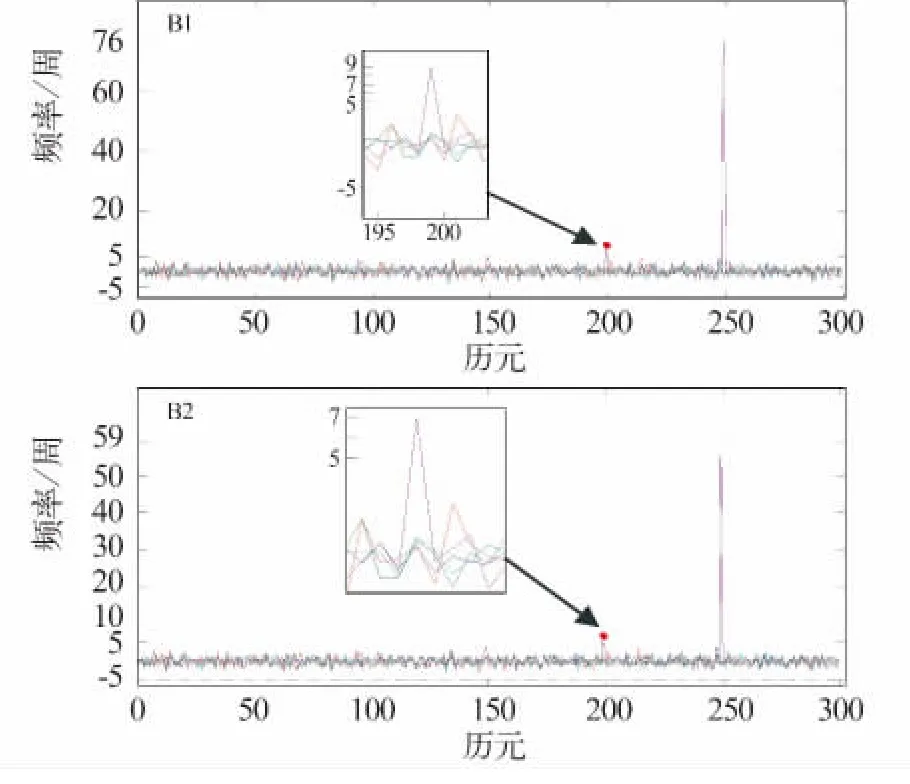
图5 加周跳的单频码相组合Fig.5 Single-frequency and code with cycle slip

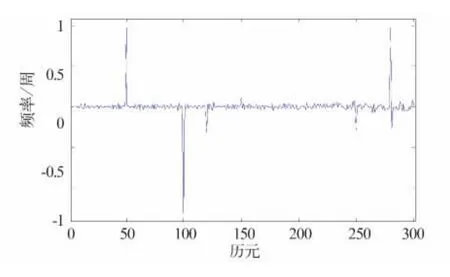
图6 基于双频载波相位的多项式拟合Fig.6 Polynomial fitting of dual-frequency and code

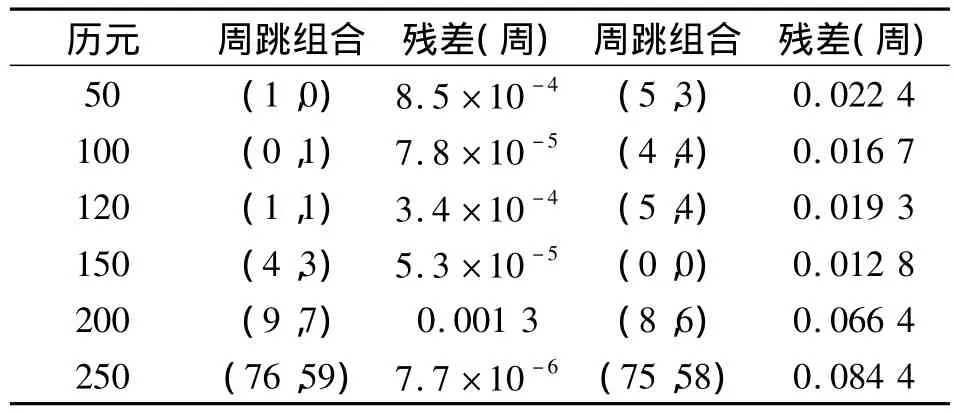
表1 周跳搜索残差对比Tab.1 Comparison of residuals of cycle slip search

5 结论

通过对北斗卫星数据的处理发现，较大的卫星钟差和伪距噪声影响了数据的质量，传统的适用于GPS周跳探测的方法如高次差法、多项式拟合法、双频码相组合法等，已不再适用于北斗周跳探测及修复。基于双频载波相位的多项式拟合法，能很好地探测周跳并修复，但存在一些探测盲点，结合单频码相组合的约束，能大大减少周跳探测盲点。考虑到周跳的整数特性，根据单频码相组合确定的搜索阈值，将周跳分为小周跳和大周跳，采用了最佳搜索算法确定周跳。算法也存在一定的不足，主要体现在对于小周跳内的探测盲点不太敏感，单频码相组合受码噪声的影响较大。

本文提出的方法主要针对静态和低动态测量的周跳探测及修复，实例分析表明，该方法能有效地探测1周以上的周跳并成功修复。该方法原理简单，易于编程实现，有一定的适用性和实用价值。

1 刘基余.GPS卫星导航定位原理与方法(第二版)［M］.北京:科学出版社，2008.(Liu Jiyu.The principle and method of navigation and positioning using GPS satellites(2nded)［M］.Beijing:Science Press，2008)

2 张成军，许其凤，李作虎.对伪距/相位组合量探测与修复周跳算法的改进［J］.测绘学报，2009，38(5):402 －407.(Zhang Chengjun，Xu Qifeng and Li Zuohu.Improving method of cycle slip detection and correction based on combination of GPS pseudo range and carrier phase observations［J］.Acta Geodaetica et Cartographica Sinica，2009，38(6):402－407)

3 蔡昌盛，高井祥.GPS周跳探测及修复的小波变换法［J］.武汉大学学报(信息科学版)，2007，32(1):39 －42.(Cai Changsheng and Gao Jingxiang.Cycle-slip detection and correction of GPS data by wavelet transform［J］.Geomatics and Information Science of Wuhan University，2007，32(1):39－42)

4 吴继忠，施闯，方荣新.TurboEdit单站GPS数据周跳探测方法的改进［J］.武汉大学学报(信息科学版)，2011，36(1):29－33.(Wu Jizhong，Shi Chuang and Fang Rongxin.Improved method based on Turbo Edit for detecting cycle slips with single GPS data［J］.Geomatics and Information Science of Wuhan University，2011，36(1):29－33)

5 陈品馨，章传银，黄昆学.用相位减伪距法和电离层残差法探测和修复周跳［J］.大地测量与地球动力学，2010，(2):120 － 123.(Chen Pinxin，Zhang Chuanyin and Huang Kunxue.Cycle slips detecting and repairing by using of phase reduce pseudorang law and ionized layer remnant method of difference［J］.Journal of Geodesy and Geodynamics，2010，(2):120－123)

6 徐锐，等.一种改进的双频单P码周跳探测与修复方法［J］.大地测量与地球动力学，2007，(4):67 －71.(Xu Rui，et al.Improved method for detecting and repairing cycle slips of dual-frequency data with single P-code［J］.Journal of Geodesy and Geodynamics，2007，(4):67 －71)

7 郑作亚，等.对Blewitt周跳探测与修复方法的改进［J］.天文学报，2005，46(2):216 － 224.(Zheng Zuoya，et al.Improving of cycle-slip detection and correction of Blewitt method［J］.Acta Astronomica Sinica，2005，46(2):216 －224)

8 李金龙，等.基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳［J］.测绘学报，2011，40(6):717－722.(Li Jinlong，et al.Real-time cycle-slip detection and repair based on code-phase combinations for GNSS triple-frequency un-differenced observations［J］.Acta Geodaetica et Cartographica Sinica，2011，40(6):717－722)

9 伍岳.第二代导航卫星多系统多频数据处理论及应用［D］.武汉大学，2005.(Wu Yue.The Theory and application on multi-frequency data processing of GNSS 2［D］.Wuhan University，2005)

10 Blewitt G.An automatic editing algorithm for GPS data［J］.Geophysical Research Letters，1990，17(3):199 －202.

AN ALGORITHM FOR CYCLE SLIPS DETECTION AND CORRECTION BASED ON COMPASS DUAL-FREQUENCY DATA

Wu Fengbo，Zhang Shubi，Zhang Qiuzhao and Hou Xiaozhen
(School of Environment Science and Spatial Information，China University of Mining and Technology，Xuzhou221116)

To counter the characteristics of Beidou navigation satellites’large clock error and signal-to-noise，a suitable combined method for cycle slips detection and correction is proposed.Firstly，the limits of two frequency cycle slip can be determined by the combination of single-frequency and code，then the least squares polynomial fitting would be performed based on dual-frequency data considering the change rate of carrier phase.The cycle slips would be demarcated and outliers would be rejected by the Blewitt method to test fitting results.The cycle slips，being an integer，can be restored by means of minimize the residuals.The test on COMPASS-MEO satellites’data verifies that the proposed algorithm can detect all cycle slips and fix it quickly in static and low-dynamic measurements.

Beidou navigation satellites;cycle slip detection;combination of single-frequency and code;ionized layer remnant method of difference;Blewitt test

P228.41

A

1671-5942(2013)05-0140-05

2012-11-12

江苏高校优势学科建设工程资助项目(PAPD SA1102)

吴丰波，男，1987年生，硕士，主要研究方向为卫星数据处理.E－mail:wu_feng_bo@163.com