桥梁变形数据小波去噪与混沌预测*

栾元重 栾亨宣 马德鹏 刘 娜 周 岩

1)山东科技大学测绘科学与工程学院，青岛 266590

2)山东科技大学机械电子工程学院，青岛 266590

3)山东科技大学资源与环境工程学院，青岛 266590

4)重庆地矿测绘院，重庆 400042

桥梁变形数据小波去噪与混沌预测*

栾元重1)栾亨宣2)马德鹏3)刘 娜4)周 岩1)

1)山东科技大学测绘科学与工程学院，青岛 266590

2)山东科技大学机械电子工程学院，青岛 266590

3)山东科技大学资源与环境工程学院，青岛 266590

4)重庆地矿测绘院，重庆 400042

跨海大桥因海浪、飓风、船体撞击等外界因素作用，桥梁变形表现为动态非线性变形状态，也存在混沌现象。为此，选择db10小波和软阈值消噪法分解与消除变形数据中的粗差与噪声，并对小波预处理后的平滑变形时间序列通过相空间重构，运用Lyapunov指数进行桥梁混沌状态判定;再将混沌时间序列预测结果与指数平滑法预测值进行分析对比，证明混沌预测可靠且精度高。

软阈值消噪法;相空间重构;Lyapunov指数;混沌时间序列;指数平滑法

1 引言

近些年，我国已有多个跨海大桥建成运营。桥梁处在海洋环境中，受海浪、飓风、船体撞击等因素的影响，使桥梁变形噪声显著，产生挠曲变形、垂直位移及水平移动，表现为动态非连续变形，还有突变、混沌现象发生。如何将桥梁变形数据噪声除去，显现出桥梁变形的特征规律;如何判定桥梁变形混沌状态，建立桥梁变形的预测模型;是桥梁变形数据处理的研究热点。

桥梁变形过程随机时间空间变化的信号，可利用小波分析对变形信息进行时频分析、奇异性探测、提取空间变形趋势项和粗差及变形信号多尺度分析。当选用合适的小波函数，经去噪处理，能消除变形数据中的高频噪声，提高变形数据预测精度。

经小波处理后的变形数据，首先计算最大Lyapunov指数并判别桥梁变形系统的混沌特征;然后选取合适的延迟时间τ和嵌入维数m，进行相空间重构;最后对混沌时间序列进行预测，实现桥梁变形预测创新。本文将混沌时间序列预测结果与指数平滑法预测值进行了分析对比，证明了混沌时间序列预测精度值较高。

2 桥梁变形数据小波分解与重构去噪

2.1 小波基函数选择

对 Haar、db6、db10、Mexican Hat小波［1］分别加入高斯白噪声的信噪比为3的blocks信号，并进行分解和低频重构去噪实验，db10小波去噪后与原测试信号相比，均方根值最小，信噪比最高，平滑度指数也最低，故本文采用db10小波函数进行桥梁变形数据预处理。

2.2 小波分解与重构去噪

将桥梁变形数据f(x)分解成不同频率成分，信号在空间Vj上投影为:

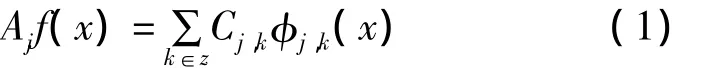
在空间Wj上的投影为:

式中Ajf(x)是信号f(x)频率不超过2－j成分，Djf(x)是频率介于2－j与2－j+1之间的成分。

矩阵形式为:

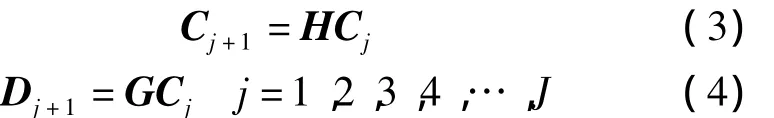
式中，H为低通滤波器，H=(hk－2n);G为带通滤波器。Mallat重构算法为:

f(x)经滤波后平滑表达式(x)为:

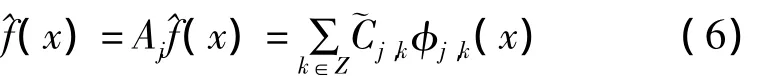
3 桥梁变形混沌特征判定

3.1 桥梁变形倍周期分叉混沌性质

当桥梁系统有扰动时，系统发生分岔并可能演变成混沌状态。取Verhulst生物模型［2］拟合桥梁变形位移时间序列，其差分方程为:

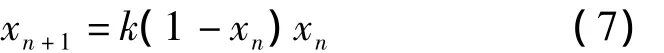
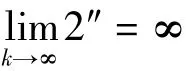
3.2 Lyapunov指数

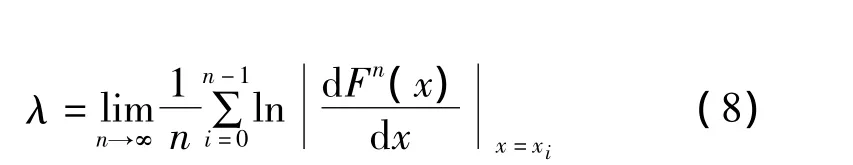
3.3 桥梁系统混沌特征判定

Lyapunov指数是用来衡量轨道收敛率或发散率。Lyapunov指数表示多次迭代中平均每次迭代引起指数分离中的度量。Lyapunov指数λ值表达式为:

进行桥梁变形混沌预测，首次应判定桥梁变形时间序列中是否具有混沌特征，表(1)列出了不同运动系统混沌特征量的判别标准。

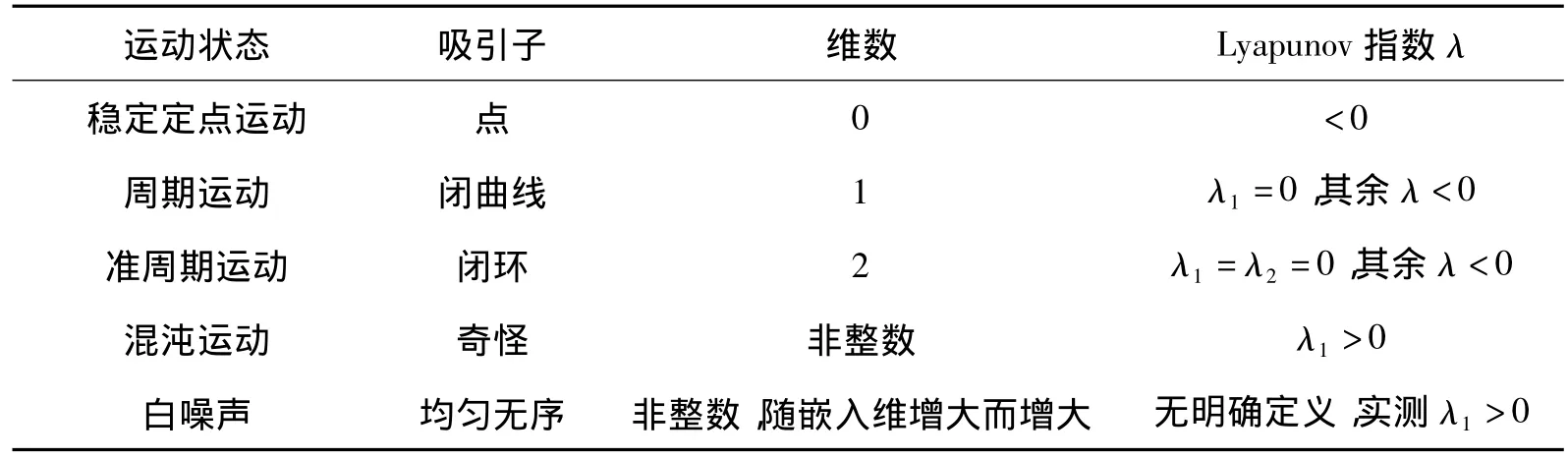
表1 各不同运动特征值取值Tab.1 Characteristic value of different movements

4 桥梁垂直变形观测数据小波去噪

取青岛跨海大桥2011年8月—2012年5月垂直变形观测数据，A1点下沉速度如图1所示。

从图1可以看到，沉降量的变化是不均匀的。在桥梁变形观测前段时间内桥梁下沉速率变化较快，而在中后期逐渐变慢。下沉的幅值前期较大，中间经过一段时间段波动到后期逐渐趋向平稳。可见从图中无法识别桥梁下沉的外界影响因素与突变点，需从小波分解图上发现其他频率的干扰波。

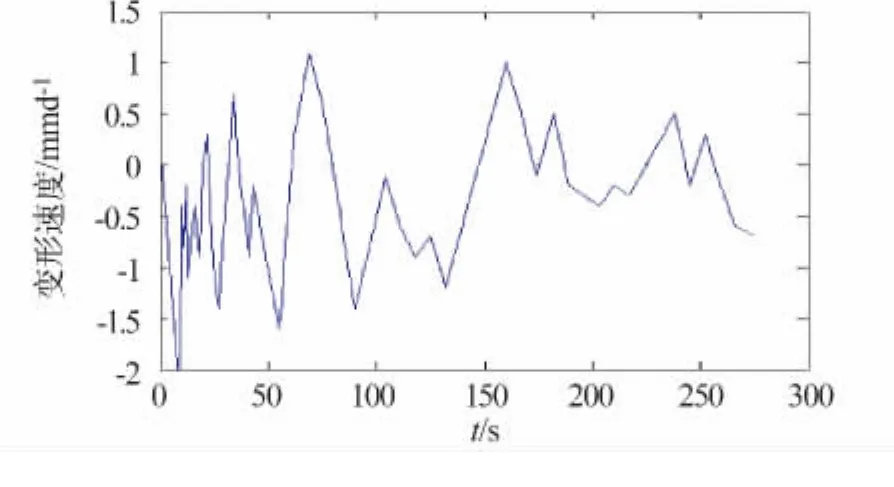
图1 下沉速度Fig.1 Deformation speed

4.1 小波阈值去噪

A1点监测数据降噪后信噪比和均方根［3］误差见表2，可见改进软阈值消噪法去噪效果最好。由图2可见，桥梁变形在去噪后，不同时期显现了不同的变形规律。

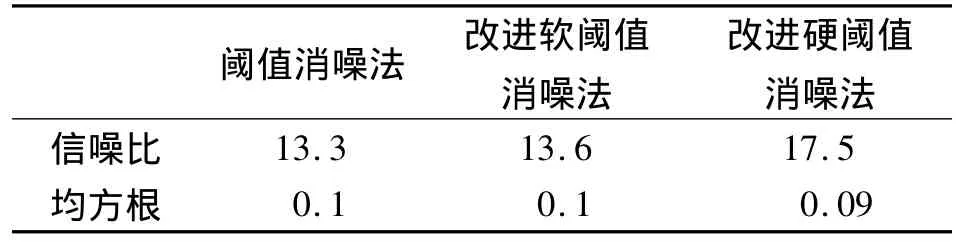
表2 不同消噪方法比较Tab.2 Comparison of different de-noising effects

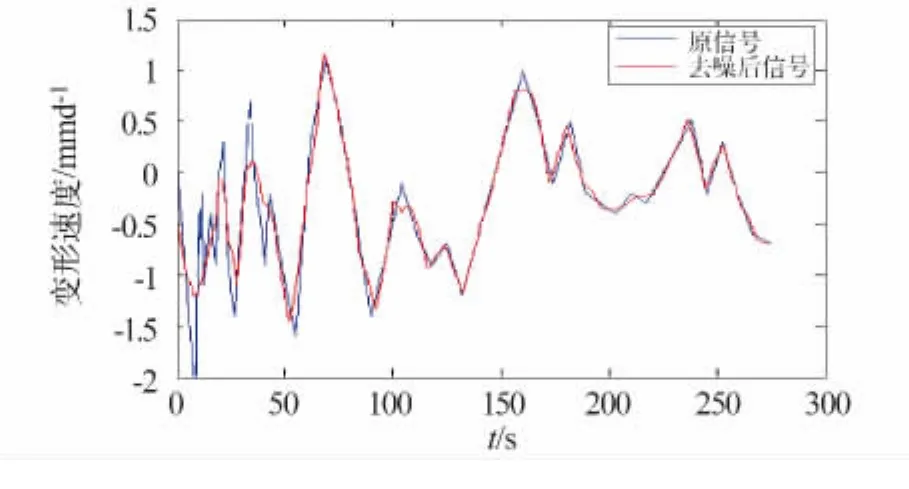
图2 去噪后与原信号对比Fig.2 Comparison between signals before and after denoising

5 消噪后桥梁变形数据混沌时间序列预测

5.1 吸引子关联维值计算

取延迟时间τ=5，作lnC(r)和lnr关系图，由图分析，当维数增加到8时，lnC(r)和lnr比值不再随m增加而改变，故取维数8为嵌入维数。经计算吸引子关联维值为2.8。

5.2 混沌特性判别

降噪后A1点监测数据，采用改进小数据量法算法，计算最大Lyapunov指数值，计算结果为2.2×10－4，大于零。

将计算吸引子关联维值和最大Lyapunov指数值，与表1中桥梁变形混沌特征判别标准对比，可见该时间序列具有混沌性质。

5.3 混沌时间序列预测

取时间序列中前 16 个数据{x1，x2，…，x16}，采用加权零阶局域法和加权一阶局域法分别对桥梁一次进行短期预测［4］，预测x17的值(表3)。

分别取指数平滑系数为0.9、0.5，采用指数平滑法［5］进行了预测，并与混沌预测结果进行对比，结果见表4。

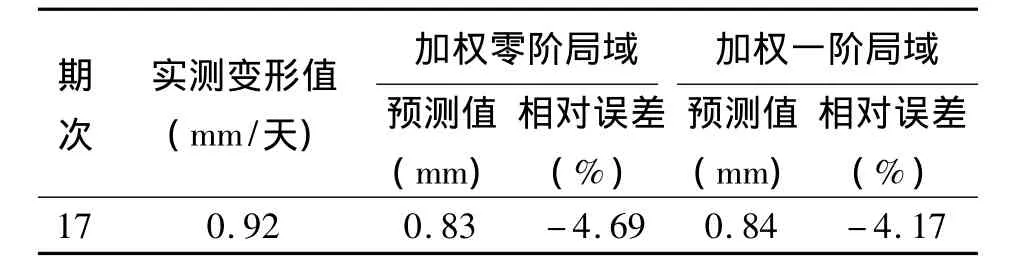
表3 混沌时间序列法预测Tab.3 Forecast of chaotic time series method

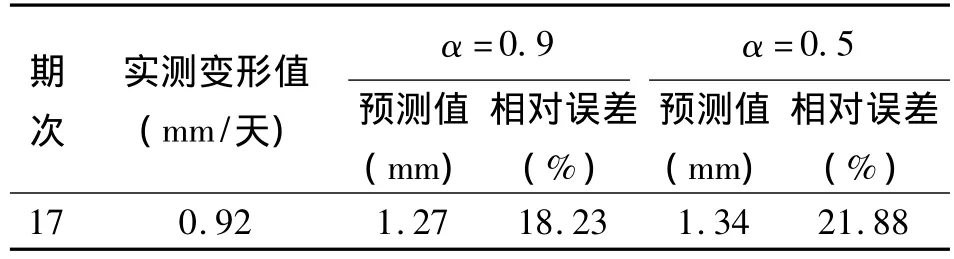
表4 指数平滑法预测Tab.4 Forecast of exponential smoothing method

通过计算结果知，加权零阶局域法和加权一阶局域法的预测误差明显小于指数平滑法，加权一阶局域法计算精度优于加权零阶局域法。预测结果表明混沌预测方法可靠、精度高，能真实地反映桥梁变形状态。

6 结论

1)对跨海大桥变形监测数据，选用db10小波函数进行桥梁预处理后，去噪效果较好，去噪后结果显示了桥梁变化规律。

2)根据桥梁混沌变形状态，提出混沌特征量计算方法，确定了桥梁变形混沌判别准则。

3)对小波去噪后的数据建立了混沌预测模型，并将混沌极差预测值与指数平滑预测值进行比较，结果显示了混沌预测方法精度较高。

1 刘云成，陈振学，马于涛.自适应阈值的小波图像去噪［J］.电光工程，2007，34(6):77 －81.(Liu Yunxue，Chen Zhenxue and Ma Yutao.Adaptive wavelet thresholding method for image denoising［J］.Opto-Electronic Engineering，2007，34(6):77 －81)

2 韩敏.混沌时间序列预测理论与方法［M］.北京:中国水利水电出版社，1996.(Han Min.Chaotic time series prediction theory and method［M］.Beijing:China Water Power Press，1996)

3 Donoho D L.De-noising by soft-thresholding［J］.IEEE Transactions on Information Theory，1995，41:613 －627.

4 徐铭陶，秦树人，陈志奎.实施一维Mallat算法的几个问题［J］.重庆大学学报，1997，20(1):7 －11.(Xu Mingtao，Qin Shuren and Chen Zhikui.Some problems about the implementat ion of one-dimensional mallat algorithm［J］.Journal of Chongqing University，1997，20(1):7 －11)

5 张忠平.指数平滑法［M］.北京:中国统计出版，1996.(Zhang Zhongping.Exponential smoothing［M］.Beijing:China Statistics Press，1996)

WAVELET DENOISING AND CHAOS PREDICTION OF BRIDGE DEFORMATION DATA

Luan Yuanzhong1)，Luan Hengxuan2)，Ma Depeng3)，Liu Na4)and Zhou Yan1)
1)College of Geomatics of SUST，Qingdao266590
2)College of Mechanical and Electronic Engineering，Shandong University of SUST，Qingdao266590
3)College of Resources and Environmental Engineering of SUST，Qingdao266590
4)Surveying and Mapping Institute of Chongqing，Chongqing400042

Due to external factors such as waves，hurricanes and ship collision，cross-sea bridge deformation shows the dynamic nonlinear state，there is also a chaotic phenomenon.Therefore，db10 wavelet threshold de-noising and soft law are used to break down and eliminate the gross errors in the data distortion and noise.Phase space is reconstructed by the smooth deformation of the time-series after wavelet pretreatment，the bridge chaos state is determined by Lyapunov indices，and chaotic time series prediction and exponential smoothing forecast are analyzed and compared，it is proved that chaos prediction has reliable and high precision.

soft threshold de-noising;phase space reconstruction;Lyapunov index;chaotic time series;exponential smoothing method

P207

A

1671-5942(2013)05-0133-04

2013-03-12

栾元重，男，1963年5月生，博士，教授，博士生导师，主要研究方向为变形数据处理理论与方法.E－mail:mdp123@163.com