基于RBF及滤波神经网络对参考站高程时间序列分析*

赵 刚 张思慧 张恒璟 黄声和 叶国凤

(辽宁工程技术大学，阜新 123000)

基于RBF及滤波神经网络对参考站高程时间序列分析*

赵 刚 张思慧 张恒璟 黄声和 叶国凤

(辽宁工程技术大学，阜新 123000)

为更好地分析IGS连续运行参考站高程数据的变化规律及其变化趋势，以及预测将来一段时间内高程数据的变化，基于RBF正则化神经网络及小波滤波神经网络理论，以MATLAB7.0为平台对北京IGS站的高程分量数据进行GRNN函数逼近和小波分解逼近。通过对历年高程数据进行拟合和分层滤波，分析发现高程时间序列存在季节变化，其是以半周年项和年周项的季节性变化，其中年周期项比较明显。

RBF;正则化;小波滤波;时间序列;GRNN函数逼近

1 引言

自从中国CORS基准站加入IGS网络观测以来，已经获取了大量的高精度连续观测数据，并对参考站的观测数据进行了大量分析。如文献［1］采用抗差最小二乘迭代与功率谱估计相结合的方法，得到了高程方向的各主周期项和振幅，并发现基准站高程方向具有接近一年的年周期运动和多于一年的第二主周期项运动，但是半周年项运动所占的比重很小。在高程数据除噪拟合问题中，由于大量数据中存在一些无效数据。如何剔除这些无效数据及如何对数据进行优化，对高程数据的误差及其函数关系的分析显得十分重要，因而一种好的数据处理方法就显得尤为重要。

目前，国内对于高程数据的误差及函数关系研究的比较多，并且取得了许多优秀的成果，但对于高程数据变化趋势的研究比较少及在处理数据时未对一些无效数据进行屏蔽［2－4］。因而，很难真实体现数据的内在规律及函数关系。与其他的数据处理方法相比，正则化RBF神经网络在处理数据时，能有效地剔除一些无用数据，并对余下的数据进行进化训练拟合，其特别适合处理数据量较大的问题。经正则化RBF神经网络处理后的数据，再经由小波分层滤波(一到六阶滤波)能有效地反映出数据的内在规律、函数关系及变化趋势［4－8］。

本文将以中国 IGS连续运行参考站北京房山(BJFS)站高程分量的时间序列数据为例，利用RBF神经网络剔除含噪的数据中的无效数据，对剩下的再生数据进行进化训练拟合，并利用小波滤波神经网络对数据进行分解逼近找出数据的变化趋势。

2 正则化RBF网络

2.1 RBF 网络

多变量插值径向基函数(RBF，Radical Basis Function)属于前向神经网络类型，它能够以任意精度逼近任意函数，特别适用于处理数据问题。

RBF网络是由一种三层前向网络组成。第一层是输入层由信号源点组成;第二层为隐含层，隐单元视所描述问题的需要而定，隐单元变换函数RBF是对中心点径向对称且衰减的非负非线性函数;第三层为输出层，它对输入模式的作用作出响应。RBF网络的基本思想:用RBF作为隐单元的“基”构成隐层空间，这样就可以将输入的矢量直接(即不需要通过权连接)映射到隐空间。当RBF的中心确定以后，这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的，即网络的输出是隐单元输出的线性加权和。此处的权即为网络可调参数。

在RBF网络中，输入层仅仅起到传输信号的作用，与其他神经网络相比，输入层和隐含层之间可以看作连接权值为1。其激活函数的一般表达式为:

2.2 正则化网络与正则化参数估计

正则化逼近函数Fλ(x)关于中心xi的Green函数的展开项系正则化网络，为

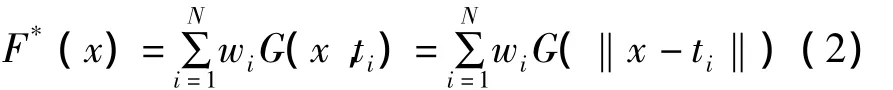
将展开项使用一组新的权值wi，使新的代价泛函数ξ(F*)值最小，即:

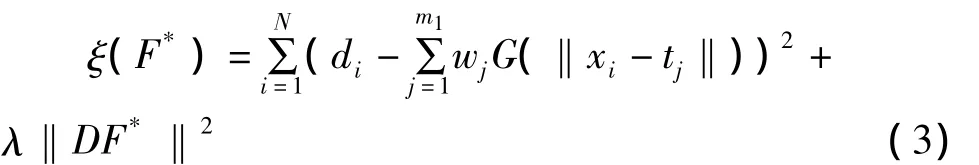
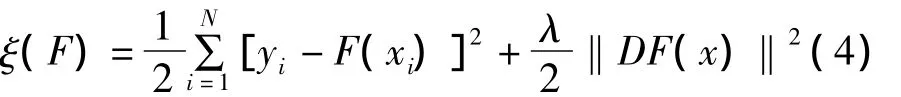
2.3 广义交叉确定

其中d为期望输出量，G为高斯插值矩阵，‖DF*‖为非线性基函数。

令Fλ(x)为f(x)相对于某个正则化参数λ的正则化估计，即Fλ(x)为使表示非线性回归问题的Tikhonov泛函数:

使用估计^R(λ)的一个缺陷是它要求知道噪声的关系δ2，在实际情况中，δ2通常是未知的，为此引入广义交叉确定，即:

其中，wk为权系数，akk=∂Fλ(xk)/∂yk，yk为数据点，V(λ)为影响矩阵。

2.4 RBF 网络逼近

由归一化的RBF网络思想、Nadaraya-Watson回归估计及Gauss分布函数可得:

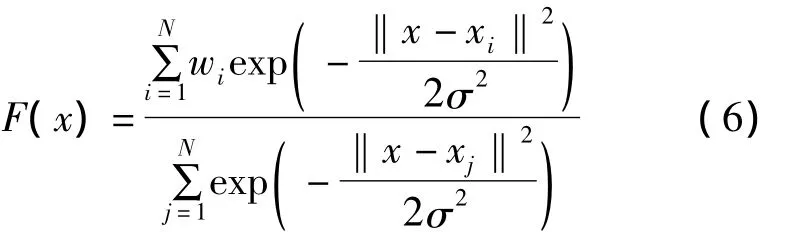
式中，xi、xj为数据点。

2.5 GRNN函数逼近MATLAB实现结果

图1 2000年和2001年GRNN函数逼近Fig.1 GRNN function approximation of 2000 and 2001

应用newgrnn()函数构建一个广义回归神经网络，基于离散数据点的情况，散布常数spread选为0.7，输入层选用53个神经元，隐含层数为3，输出层为1个神经元，训练目标为0，学习速度为1。对输入数据训练后应用sim()函数进行仿真，得到结果如图1所示(以2000和2001年为例)。其中“目标”是原始数据，“输出”为由RBF正则化函数逼近的数据处理后所得的函数图像，其SSE值分别为0.000 178 65和0.001 793 6，拟合效果理想。2000和2001年的图像变化趋势大体相同，1—4月参考站测得的数据波动较小，为87.44～87.45;5—8月参考站测得的高程相对于前四个月增长比较多，其范围在87.45～87.47;9—12月所得的数据变化趋势与1—4月的相似。表现出了年周期、半年性和季节性变化，且其年周期性约为1年，具有向上斜趋势。

3 数据处理

基于北京房山站2000—2004年高程时间序列，采用小波滤波，其中数据采样方法采用Shannon采样定理，滤波函数选用快速 Fourier 函数［9，10］，结果如图2所示。

由图2中的a1～a5可知，高程数据不是受单一因素的影响而是受多因素的影响。数据的变化趋势是:刚开始所得的数据值逐步变大，到达一定值保持一段时间后又开始下降。从a1(即一阶滤波)可知，高程时间序列的倾斜趋势不明显，即高程随时间的增长非常缓慢甚至不增长，如2000和2004年;由a2和a3可知，高程时间序列的波动较大，表现出较为明显的随机性，季周期性不明显;从a4可知，该高程时间序列表现出半年周期性，但其半年周期性波动较大，即半年周期性不明显;从a5可知，该高程时间序列的年周期性最为明显且波动较小，表现出较好的年周期性;从a6可以看出高程时间序列滤波效果很不理想，说明该高程时间序列为低阶时间序列。通过对历年数据的分析可预测未来参考站高程数据变化趋势。

4 结论

1)参考站观测的2000和2001年高程数据表现出了年周期、半年性和季节性变化，且其年周期性约为1年，具有一定的向上趋势。

2)北京房山站高程数据不是受单一因素的影响而是受多因素的影响。参考站观测的高程数据的年周性比半周年性更明显。北京房山站高程时间序列具有向上趋势，但向上趋势不明显且存在着波动性，即随着时间的变化，高程数据增长缓慢;该高程数据具有明显的随机性，即该时间序列为非线性时间序列，在对其进行拟合时得采用非线性数学处理方法;从a6可以看出高程时间序列滤波效果很不理想，说明该高程时间序列为低阶时间序列。

图2 2000—2004年高程数据的小波分解逼近示意图Fig.2 The wavelet approximation of elevation data map from 2000 to 2004

1 张恒璟，程鹏飞，郭英.我国IGS基准站高程时间序列抗差功率谱估计［J］.测绘科学，2012，37(3):52－53.(Zhang Hengjing，Cheng Pengfei and Guo Ying.Robust power spectrum estimation on height time series of Chinese CORSstation［J］.Science of Surveying and Mapping，2012，37(3):52－53)

2 丁明军，等.近10年青藏高原高寒草地物候时空变化特征分析［J］.科学通报，2012，57(33):3 185 －3 194.(Ding Mingjun，et al.Spatiotemporal variation in alpine grassland phenology in the Qinghai-Tibet Plateau from 1999 to 2009［J］.Chin Sci Bull.，2012，57(33):3 185 － 3 194.doi:10.1007/s11434-012-5407-5.

3 刘禹，蔡秋芳，宋慧明.青藏高原中东部2485年来温度变化幅度、速率、周期、原因及未来趋势［J］.科学通报，2011，56(25):2 042 － 2 051.(Liu Yu，Chai Qiufang and Song Huiming.2485 years in East Qinghai-Tibet plateau amplitude，rate of temperature change，cycle，cause and future trends［J］.Chinese Science Bulletin，2011，56(25):2 042－2 051)

4 张恒璟，程鹏飞.基于GPS高程时间序列粗差的抗差探测与插补研究［J］.大地测量与地球动力学，2011，(4):72 － 73.(Zhang Hengjing and Chen Pengfei.Study on robust detection and interpolation from gross errors of GPS height time series［J］.Journal of Geodesy and Geodynamics，2011，(4):72 －73)

5 黄俊华，陈文森.连续运行卫星定位综合服务系统建设与应用［M］.北京:科学出版社，2009.(Huang Junhua and Chen Wenshen.Continuously operating GPS comprehensive service system construction and application［M］.Beijing:Science Press，2009)

6 徐文兵.GPS连续运行参考站系统(CORS)定位精度的可靠性研究［D］.合肥工业大学，2009.(Xu Wenbing.Research on positioning reliability for GPS continuously operating reference station system［D］.Hefei TechnologicalUniversity，2009)

7 张恒璟，程鹏飞.基于经验模式分解的CORS站高程时间序列分析［J］.大地测量与地球动力学，2012，(3):133－134.(Zhang Hengjing and Cheng Pengfei.Analysis on time series of two CORS stations’height based on EMD［J］.Journal of Geodesy and Geodynamics，2012，(3):133 －134)

8 乔学军，等.中国大陆GPS基准站的时间序列特征［J］.武汉大学学报(信息科学版)，2003，28(4):414－416.(Qiao Xuejun，et al.Time series characteristic of GPS fiducial stations in China［J］.Geomatics and Information Science of Wuhan University，2003，28(4):414 －416)

9 姚展予，等.大气波导特征分析及其对电磁波传播的影响［J］.气象学报，2000，58(5):606 － 610.(Yao Zhanyu，Zhao Bolin and Li Wanbiao.The analysis on characteristics of atmospheric duct and its effects on the propagation of electromagnetic wave［J］.Acta Meteorologica Sinica，2000，58(5):606－610)

10 周东旭，等.GPS接受机仪器偏差的长期变化特性分析［J］.大地测量与地球动力学，2011，(5):115 －117.(Zhuo Dongxu，et al.Analysis of long-term variations of GPS receivers’differential code bias［J］.Journal of Geodesy and Geodynamics，2011，(5):115－117)

ANALYSIS ON HEIGHT TIME SERIES OF IGS BASED ON RBF AND FILTERING NEURAL NETWORK

Zhao Gang，Zhang Sihui，Zhang Hengjing，Huang Shenghe and Ye Guofeng
(School of Geomatics，Liaoning Technical University，Fuxin123000)

In order to analyze the change law and tendency of height data of IGS continuous operation reference station and predict the future changes of the height data over a period of time，based on the theories of RBF regularization neural network and wavelet filter neural networks，the height component data of Beijing IGS station is dealt with the GRNN function approximation and wavelet decomposition approximation on the basis of the MATLAB7.0 platform.According to the fitting historical height data and hierarchical filtering，the seasonal changes were found in height time series，and seasonal changes included half year cycle changes and year cycle changes，and the year cycle was obvious.

RBF;regularization;wavelet filtering;time series;GRNN function approximation

P207

A

1671-5942(2013)05-0136-04

2013-01-20

国家基础测绘项目(50474032);辽宁工程技术大学优秀青年基金(09－259)

赵刚，男，副教授，硕士生导师，研究方向为空间大地测量数据处理.E－mail:541534583@qq.com