基于遗传算法的高维子空间聚类算法设计

黄白梅，章 政

（武汉科技大学 信息科学与工程学院，湖北 武汉 430081）

在现实世界中，高维数据占据着主导地位，例如文档数据、WEB数据、基因微阵列数据、网络通信数据等数据经常达到上千维甚至更高。在对高维数据进行聚类时，由于受到“维数灾难效应”[1-2]的影响，同时高维数据空间中的一些不相关属性维掩盖了要寻找的目标簇，使得传统的聚类算法在高维数据空间上进行聚类分析时失效。因此需要高维降维去掉不相关属性维，通过对解空间中的全部属性子集进行搜索，进而找到最密集的优良子集，再在低维空间中进行聚类分析。

传统的搜索算法诸如贪婪算法等，在对其进行聚类分析时非常容易陷入局部最优解的困境而达不到理想的要求。遗传算法是一种自适应全局优化的概率搜索算法，它在理论上可以克服局部最优解而搜索到全局最优解，因此被广泛的应用于解决复杂的优化问题。

文中针对高维数据的特点，为了降低“维数灾难效应”对聚类结果的影响，构建了一个基于遗传算法进行高维数据聚类的框架，利用遗传算法的全局搜索能力，挖掘高维数据空间中密集度高的数据子集，然后再在这个子集上进行聚类分析。

1 子空间聚类概述

目前对高维数据进行聚类的方法主要还是基于子空间聚类和全空间降维这两个方面。

子空间聚类的方法（Sub-space Clustering）[2-5]是属性子集选择的一种扩展，在高维聚类方面显示出了其独有的优势。它的基本思想是基于不同子空间可能包含不同的、有意义的类或簇，它在相同的数据集的不同子空间中搜索类或簇群，因此可以通过抽取出存在于子空间的类或簇来进行聚类分析。子空间聚类为每个类或簇搜索出其对应的子空间。根据搜索策略的不同，可以将子空间聚类方法划分成为两大类：自底向上的搜索方法（如 CLIQUE算法[3]）和自顶向下的搜索方法（如PROCLUS算法[4]）。也有一些算法结合自底向上的搜索方法和自顶向下的搜索方法（如 DOC算法[5]）。子空间聚类方法对于处理不同类或簇存在于不同子空间里的高维数据结构模型比较有效，不过这类方法的计算复杂性非常高。

全空间降维则是通过缩减维数将高维数据空间归约到较低维数据空间，然后再通过传统的方法进行聚类分析，这类方法是在一个特征子空间里面寻找所有的类或簇，但是忽略了在高维数据空间里面不同的类或簇可能有不同的特征子空间。

这两种聚类方法都有其优点与不足，目前尚没有一种算法能够适用于所有的情况，在实际应用中，我们应该根据具体问题的特点来选择合适的聚类算法。同时由于在处理大规模高维数据时，容易陷入局部最优解的状况。因此经常采用将各种全局优化搜索算法，如遗传算法，粒子群算法，蚁群算法等，结合子空间聚类或者降维来处理的策略，达到最终寻找到最优解。遗传算法（GA）[6]，是通过模拟孟德尔.摩根的群体遗传学说、达尔文的生物进化论的自然选择和遗传学机理的生物进化过程而形成的一种自适应全局优化概率搜索算法。它是一种高效的全局优化搜索算法，已被许多研究者应用到聚类分析中。

2 基于遗传算法的子空间聚类算法

基于遗传算法进行高维聚类的新算法利用遗传算法的全局搜索能力对高维数据的特征空间进行搜索，因此其基本流程跟传统的遗传算法大致相同[7]。组成种群的个体由特征维和类中心点两部分经过编码后组成，每个个体对应着一个特征子空间；适应度值是遗传算法对搜索进行评估的唯一依据，新算法中的适应度值表示个体所代表的特征子空间进行聚类的效果，适应度值越大，表明子空间数据对象的密集性越强，聚类越好。

2.1 编码与初始化

常用的编码方式有二进制编码和实数编码等，由于二进制编码的染色体长度相对较长，且编码的种群稳定性比实数编码要差，文中选取实数编码。个体的编码空间[8]由（SUB，CEN）这两部分组成，其中SUB代表特征子空间的实数编码串，CEN代表类中心的实数编码串。初始种群我们采用随机生成的策略。随机的选取（最大的特征维数目）个特征维和（最大的类数目）个数据对象进行编码组成个体，然后迭代（预设的初始种群的规模）次，即完成初始种群的产生。

初始种群随机生成的方案如下：随机的在数据对象集中选取m个特征维的编号和n个数据对象的编号来进行编码，构成初始染色体。例如某数据对象集有10维，由150个数据对象组成。取m=4，n=3，则一个染色体的基因即由4个特征维的编号和3个数据对象的编号组成。染色体的左部分基因表示由第5，8，3，2等4个特征维组成，染色体的右部分基因表示由该数据集的第32，12，50个数据组成，两部分共同构成了一个染色体。通过编码即完成了染色体的构造。

2.2 适应度函数的设计

适应度值是遗传算法进行搜索的唯一依据，因此适应度函数设计的好坏直接影响着算法的搜索方向及收敛程度。本文基于类内距离，类间距离和信息熵提出了一种新的适应度评估函数。

在高维数据聚类中，目标簇通常只跟某些特征维有关，为了考察特征维在子空间聚类中所表现出来的性能，本文提出用特征维对子空间聚类的贡献率来表征。

假设某子空间中含有 K个以{C1，C2，…，CK}为中心的类{A1，A2，…，AK}，对每一个类 Ai（i=1，2，…，K），考虑 3 个函数：

在这里，T表示数据集的数据对象个数，Ti表示数据集的第i个类的数据对象的个数，表示第i个类的中心点的第j维值，表示第n个类内第n个数据对象的第j维值。

fitness1ji体现了第j维对类 Ai的类内贡献率-越小，表示第i类内某个数据对象的第j维值与中心点的第j维值距离越接近，fitness1ji就越大。则类Ai在特征维j上是稠密的，即称维j对类i的贡献大，反之，称维j对类的贡献小。

故维j对类i的贡献率为：

维j对此子空间聚类的贡献率：

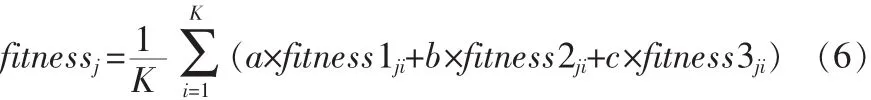
染色体（特征子空间）的适应度值：

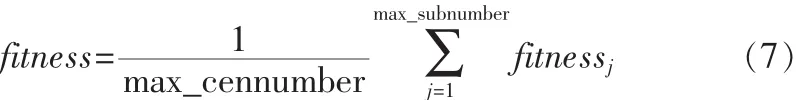
其中max_cennumber表示最大的特征维数目，max_cennumber表示最大的类数目a，b，c。为常数（在这里根据先验知识取 a=1，b=-0.5，c=0.8）。

2.3 遗传算子及控制参数

遗传操作是遗传算法的核心部分，遗传操作有3个操作算子：选择算子、交叉算子和变异算子，父代种群通过遗传操作产生出子代种群来繁衍和进化[9]。

选择算子：文中依据上述适应度函数作为选择的依据，保留部分适应度函数值高的优良个体（根据先验知识预先设定），进入到子代进行繁殖，然后采取轮盘赌选择法，根据适应度函数值的大小选择剩下的个体[8]。

交叉算子：交叉算子的主要参数是交叉概率pc，取pc⊂[0.4，0.9]，根据pc对父代个体进行单点交叉操作[8]，在基因位上通过互换基因，生成两个新的子代个体。

变异算子：文中取基本位变异法[9]，按照预设的变异概率pm进行变异操作，在基因位上对原基因值进行突变替换。pm取 0.01～0.2

迭代终止条件：采用世代数是否超过预设的参数值[11]的方法来作为遗传算法终止的条件。

3 实验对比与分析

为了验证文中提出的基于遗传算法进行高维聚类的新算法的聚类效果和性能，采用了一组真实数据集来进行实验。在实验中我们选取了经典的聚类算法k-means算法，子空间聚类算法PROCLUS[11]算法以及基于遗传算法进行高维数据数据聚类的降维算法GA-HDclustering算法[8]与本文提出的算法进行了比较。通过比较错误率 （Error_degree），熵（Entropy）值，纯度（Purity）值，Rand 统计量（RI）值这几项指标的评判值来对其聚类结果进行评估和比较。

为了检验文中算法在实际高维数据中的有效性，选取了一组真实的数据集来进行实验。数据集来自UCI机器学习的数据集（http://archive.ics.uci.edu/ml/），如表 1。

表1 真实数据集Tab.1 Real data set

该数据集最初是用来对乳腺癌病进行预测和诊断的。wdbc数据集记录了569位女性的乳房肿块的30个特征值，这些特征值是通过乳房肿块的细针抽取数字图像而计算出来的，它们体现了图像中细胞核的特征。根据这30个特征值，可以将这569位女性分为两类，一类患有乳腺癌者，共有212人；另一类未患乳腺癌者，共有357人。数据集客观上分为两类。

对于wdbc数据集，对其使用k-means算法、PROCLUS算法、GA-HDclustering算法以及文中提出的基于遗传算法进行高维聚类的新算法分别进行实验。运行GA-HDclustering算法和基于遗传算法进行高维聚类的新算法时，为了便于比较，将需要设定的相关参数，此处取pc=0.8，pc=0.02，max_subnumber=25，max_cennunber=2，popsize=80，max_gen=350。

对这组数据集分别运行k-means算法、PROCLUS算法、GA-HDclustering算法以及基于遗传算法进行高维聚类的新算法，计算各自的错误率并统计熵值、纯度值以及Rand统计量值这3个有效性衡量指标，具体的实验结果与分析如下。

数据集客观上分为两类，共有569个数据对象，每个数据对象有30维，各类分布如下：（各类数据对象数目）Class1:357，Class2:212。

各算法在对wdbc数据集聚类对应的特征子空间如表2所示。

表2 数据集的聚类特征子空间Tab.2 Clustering feature sub-space of

我们将每个算法的错误率标记为Error。k-means算法，PROCLUS算法，GA-HDclustering算法和基于遗传算法进行高维聚类的新算法的错误率如表3所示。

表3 各个算法的错误率Tab.3 Error rate of each algorithm

通过上面4个算法对数据的聚类结果，看到基于遗传算法进行高维聚类的新算法的错误率为0.143 2，比K-means算法的0.151 6和PROCLUS算法的0.153 4这两个经典算法的总错误率要小得多，比GA-HDclustering算法的总错误率0.151 2也明显偏小，聚类的精确性最高。

各算法在对该数据集进行聚类时，对应的熵值，纯度，RAND统计量如表4所示。

表4 各个算法对应的熵值、纯度和RAND值Tab.4 Entropy，purity and RI of each algorithm

实验结果说明，K－means算法和PROCLUS算法的熵值优于GA－HDclustering算法，K－means算法的纯度和 RI值比PROCLUS算法和GA－HDclustering算法也略高。而基于遗传算法进行高维聚类的新算法的熵值比这3个算法大幅度降低，纯度和RI值也比这3个算法明显提高。

4 结束语

文中提出的算法能够高效地对高维数据进行降维，找到有效的特征子空间进行聚类；并且对数据进行聚类结果的错误率和评估指标Entropy值、purity值及RI值与其他算法相比，精确性和鲁棒性更强；综上所述，文中提出的算法能够有效地进行高维数据聚类，降低“维数灾难效应”的影响，是一种行之有效的高维数据聚类方法。但同时也存在一些问题值得进一步深入研究，文中提出的算法中的各个参数一般都是根据经验及多次试验进行设定的，下一步考虑研究各参数及其自动设置，另外该算法在对非特定的真实数据进行聚类时的鲁棒性仍有待提高。

[1]Donoho D L.High-dimensional data analysis:the curses and blessings of dimensionality[C]//Aide-Memoire of a Lecture at AMS Conference on Math Challenges of 21st Century，2000.

[2]Parsons L，Haque E，Liu H.Subspace clustering for high dimensional data:a review[J].SIGKDD Explorations，2004，6（1）:90－105.

[3]Agrawal R，Gehrke J，Gunopulos D.Automatic subspace clustering ofhigh dimensionaldata fordata mining applications[J].In Proc.ACM－SIGMOD Int.Conf.Management of Data （SIGMOD'98），（Seattle， WA），1998:94－105.

[4]Aggarwal C C，Procopiuc C.Fast algorithms for projected clustering[Z].In Proc.of ACM SIGMOD，1999.

[5]Procopiuc C M，Jones M，Agarwal P K，et al.A monte carlo algorithm for fast projective clustering[Z].Proc.ACM SIGMOD，2002.

[6]Galletly J E.An overview of genetic algorithms[J].Kybernetics，1992， 21（6）:26－30.

[7]周明，孙树栋.遗传算法原理及应用[M].国防工业出版社，1999.

[8]孙浩军，熊琅环.一种高维数据聚类遗传算法[J].计算机科学与工程，2010，32（8）:94－98.

SUN Hao-jun，XIONG Lang-huan.A genetic algorithm for hign-domensional data clustering[J].Computer Science and Engineering，2010，32（8）:94－98.

[9]潘正君，康立山，陈毓屏.演化计算[M].北京：清华大学出版社，1998.

[10]何宏，谭永红.一种基于动态遗传算法的聚类新方法[J].电子学报，2012，2（2）:254－260.

HE Hong，TAN Yong-hong.A novel clustering method based ondynamicgeneticalgorithm[J].ChineseJournalofElectronics，2012，2（2）:254－260.

[11]Aggarwal C C，Procopiuc C.Fast algorithms for projected clustering[Z].In Proc.of ACM SIGMOD，2004.