基于卡尔曼滤波与Mean Shift的运动车辆跟踪

张秀林 ， 王浩全 ， 刘 玉 ， 安 然

（1.中北大学 动态测试技术重点实验室，山西 太原 030051；2.中北大学 信息与通信工程学院，山西 太原 030051）

在Mean Shift跟踪算法中，Changjiang Yang[1]对多维图像的Mean shift方法进行了讨论，使用改进的快速高斯变换提高算法的速度，Collins[2]将尺度空间和 Mean shift相结合解决了核函数带宽实时变化时的目标跟踪。但是，核窗宽决定了参与Mean-Shift迭代的样本数量，而且也反映了跟踪窗口的大小，在整个跟踪过程中不再发生变化[3-4]。 因此，当目标存在明显尺度变化的时候，尤其是当目标尺寸逐渐增大以至超出核窗宽范围的时候，固定不变的核窗宽常常会导致目标的丢失。

1 颜色特征的卡尔曼滤波对目标初步预测

卡尔曼滤波器初预测算法流程：

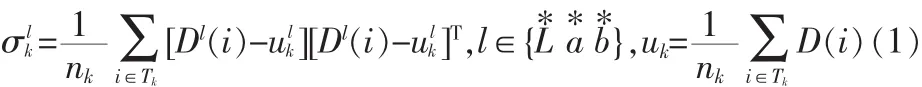
其中，D（i）表示像素i的颜色值，uk表示第k个聚类颜色模型的均值，Tk表示属于第k个聚类的像素集合，nk表示第 k个聚类包含的像素数。

第k个聚类的高斯模型：

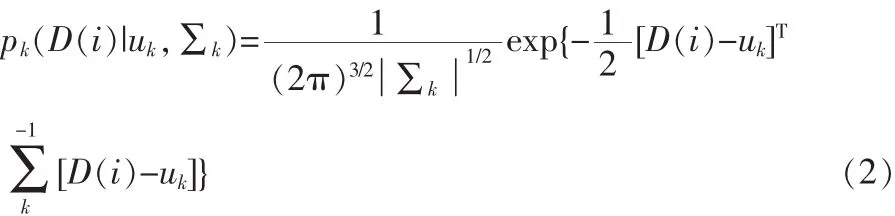
第k个聚类在目标颜色分布中的权重：

第k个聚类的归一化权值：

田志芳立即慌了，她发现杨连长也在，他是和刀营长骑马提前来的，但他胸前没挂红花。她扭过头问向阳花：“谁？谁结婚？”向阳花笑嘻嘻地说：“别急，妹子，你今天仔细找找，这里还有比杨连长更好的不？”

计算目标模型：

Step3:使用3种尺寸的窗口搜索候选目标以适应尺度上的变化。运动车辆的中心在X、Y轴上的运动是一个由随机加速而被扰动的直线运动。

其中，（x，y）表示矩形中心的坐标，t近似为视频序列的帧数，和分别是矩形中心在 x和 y方向的运动速度，w（t）和v（t）是两个相互独立的零均值高斯白噪声序列，分别表示状态转移噪声和观测噪声。

Step4:计算候选目标区域中每个聚类的权值：

计算直方图的相似性:

2 基于Mean Shift算法寻找目标真实的位置

在起始帧中Epanechikov核函数作用的区域称为目标区域，起始帧中的卡尔曼滤波的矩形框中心确定后，目标区域的中心（核函数的中心坐标）、目标区域的大小（等于核函数的带宽）就可以确定了。将像素的灰度u作为特征值，分别对目标与背景的特征值建立归一化直方图[6]。

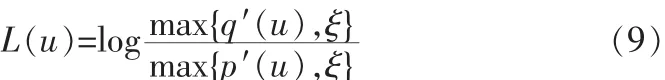
q′（u）、p′（u）分别为为目标中灰度特征值 u 在目标归一化灰度直方图中的取值和背景中灰度特征值u在背景归一化灰度直方图中的取值；ξ满足：logξ≤L（u）≤-logξ；采用 λu=（L（u）+logξ）/2logξ，将 L（u）转换为[0，1]范围内核直方图的带权因子。

基于Mean Shift和卡尔曼滤波相结合的跟踪算法流程：

Step1:起始帧中的卡尔曼滤波的矩形框中心x0确定后，得到核函数作用区域特征值u=1……m估计的概率密度：

其中，h为核函数的带宽，k（x）为核函数的轮廓函数，δ（x）是 Delta 函数。

Step2:根据矩形窗中心的位置，卡尔曼滤波预测下一帧中矩形窗中心的位置（x，y），当前帧目标中心的位置作为前一帧中目标中心的位置y0。

Step3:目标候选区域内的像素为{xi}i=1，2，3…nk，从y0这一点开始寻找核函数的中心坐标（也就是最优匹配的目标中心为y）。计算视频对象的概率分布模型：

Bhattacharyya系数[7]近似为:

Step4:计算权值：

Step5:利用Mean Shift计算新的漂移位置

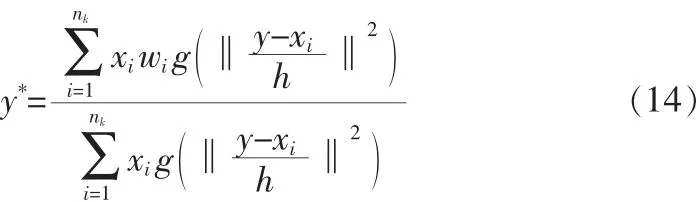
Step6:Mean Shift算法在（x，y）的邻域内寻找目标真实的位置得到（x*，y*）作为矩形窗中心的位置，转到 Step2处执行。

3 遮挡问题的处理

通过分析卡尔曼滤波器关于目标位置的估计值和由Mean Shift算法得到的卡尔曼滤波器的观测值之间残差[8]的大小来判断是否出现了大比例的遮挡。当前帧中目标中心位置估计值为{x（t），y（t）}， Mean Shift算法寻找到的目标中心真实位置为{x*（t），y*（t）}，通过{x*（t），y*（t）}得到的卡尔曼观测值为{X*（t），Y*（t）}。

滤波残差为：

设门限值γ，如果σ（t）＞γ，卡尔曼滤波器停止工作。利用前几帧Mean Shift收敛点的位置线性预测下一帧可能起始点的值{x（t），y（t）}，然后在这个起始点邻域内利用 Mean Shift算法寻找当前帧目标的位置{x*（t），y*（t）}，求当前观测值{X*（t），Y*（t）}和起始点位置{x（t），y（t）}的残差 σ（t），与 γ 进行比较。如果σ（t）＜γ，下一帧卡尔曼滤波器重新开始工作。

4 实验结果与分析

对快速运动车辆的视频序列 （遮挡问题）进行了跟踪测试。图1 Mean Shift算法对快速运动车辆（遮挡问题）的跟踪效果，第62帧和81帧车速较慢、第78帧只有小比例遮挡，能够实现正确的跟踪；第70帧和第93帧车速加快、第79帧和第80帧大比例遮挡，算法失去了对快速运动车辆的跟踪。图2本文算法的跟踪效果，有一些帧为全部遮挡，方框没有随意发散，在局部范围内移动。新算法能够始终实现对快速运动车辆（遮挡问题）的跟踪。

5 结 论

文中提出了一种卡尔曼滤波中集成Mean Shift算法的目标跟踪算法。该算法根据目标主要颜色的分布建立目标模型，用较少的参数对目标进行准确的描述，从而根据目标尺度的改变来调整卡尔曼滤波中矩形窗的大小，来弥补Mean Shift算法中窗口不变的缺陷。通过卡尔曼滤波初步预测了当前帧目标中心的位置，基于核直方图的Mean Shift算法在这点的邻域内寻找目标真实的位置，在目标出现大比例遮挡情况时，利用卡尔曼残差来关闭和打开卡尔曼滤波器，充分利用目标位置的线性预测替代卡尔曼的作用，提高了跟踪算法的鲁棒性。实验表明该算法在目标尺度变化、目标被部分遮挡、完全遮挡等情况下对快速运动的目标能够取得较好的跟踪效果。

图1 Mean Shift算法对快速运动车辆的跟踪效果：遮挡问题Fig.1 Mean Shift algorithm tracking of fast moving vehicles:occlusion

图2 本文算法对快速运动车辆的跟踪效果：遮挡问题Fig.2 Algorithm tracking of fast moving vehicles:occlusion

[1]Changjiang YANG，Ramani DURAISWAMI， Larry DAVIS.Similarity measure for nonparametric kerneldensity based object tracking[C]//Eighteenth Annual Conference on Neural Information Processing Systems Victoria， British Columbia，Canada：NIPS，2004.

[2]Robert T.COLLINS.Mean-shift blob tracking through scale space[J].IEEEComputerSocietyConferenceonComputerVision and Pattern Recognition （CVPR ’03），2003（2）：234-240.

[3]Comaniciu D，Ramesh V，Meer P.Real-Time tracking of nonrigid objects using mean shift[J].In:Werner B，ed.IEEE Int’ l Proc.of the Computer Vision and Pattern Recognition，Stoughton:Printing House，2000（2）：142-149.

[4]Yilmaz A，Shafique K，Shah M.Target tracking in airborne forward looking infrared imagery[J].Int’l Journal of Image and Vision Computing，2003，21（7）:623-635.

[5]陶新民，徐晶，杨立标，等.一种改进的粒子群和k均值混合聚类算法[J].电子与信息学报.2010，32（1）:92-97.

TAO Xin-min，XU Jing，YANG Li-biao，etal.Improved cluster algorithm based on K-Means and particle swarm optimization[J].JournalofElectronics&InformationTechnology，2010，32（1）:92-97.

[6]王田，刘伟宁，韩广良，等.基于改进mean shift的目标跟踪算法[J].液晶与显示，2012，27（3）:396-399.

WANG Tian，LIU Wei-ning，HAN Guang-liang，et al.Target tracking algorithm based on improved meanshift[J].Chinese Journal of Liquid Crystals and Displays，2012，27（3）:396-399.

[7]赵欣，陈峰，吴立知.一种改进的 mean shift运动目标跟踪算法[J].通信技术.2011，11（44）:76-79.

ZHAO Xin，CHEN Feng，WU Li-zhi.An improved mean shift moving target tracking algorithm[J]. Communications Technology，2011，11（44）:76-79.

[8]朱胜利，朱善安，李旭超.快速运动目标的Mean shift跟踪算法[J].光电工程，2006，33（5）:66-70.

ZHU Sheng-li，ZHU Shan-an，LI Xu-chao.Algorithm for tracking of fast motion objects with Mean shift[J].Opto-Electronic Engineering，2006，33（5）:66-70.