错在哪里
2013-09-17 01:14:44申祝平
中学数学教学 2013年6期
1 陕西师大附中
申祝平 (邮编:710061)
题目 已知偶函数f(x)的定义域是(-2,2),且在[0,2)上为减函数,f(m-1)>f(1-2m),求m的取值范围.
评注 本题所包含的条件很多,由常规思路,则需按m-1,1-2m的正负性来分类讨论,而其中所涉及的情形有四种.如此一来,不但过程复杂,运算也很繁冗.
如何避免讨论,优化运算,做到简化解题过程?下面,我们利用偶函数的一个性质,给出一个“一网打尽”的解法:
简洁解法 因为f(x)是偶函数,
所以f(x)=f(-x)=f(|x|),f(m-1)=f(|m-1|),f(1-2m)=f(|1-2m|).

解答错了!错在哪里?
错在 “简洁解法”省略了“求出不等式组里各个不等式的解”的过程.这不是简洁!是不完整.且因为“跳步”太快把答案弄错了.
评注错了!错在哪里?
错在 无端认定“由常规思路,则需……涉及的情形有四种.……不但过程复杂,运算也很繁冗”.
实际上,依题意,弄明白f(m-1)>f(1-2m)的三层意思:
(1)m-1在定义域内,
(2)1-2m在定义域内,
(3)|m-1|<|1-2m|,
根本不需要分四种情形讨论!
下面是一个正确、完整而简明的常规解答.

注意 解题首先要正确!其次,不要随意贬低常规思路.
2 安徽省灵璧第一中学
郑 良 (邮编:234200)
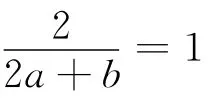
以上解法为《2014优化探究》(教师用书)第18面给出的.
解答错了!错在哪里?

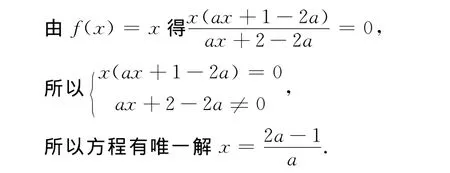
(2)当x=0,ax+2-2a=0,解得a=1,此时b=0,此时f(x)=,符合题意.
3 安徽省合肥六中
黄海波 (邮编:230001)

解答错了!错在哪里?

则g(x)=x2-mx-3.当|m|≤2时f(x)在区间(a,b)上都为“凸函数”等价于当|m|≤2时g(x)=x2-mx-3<0恒成立.
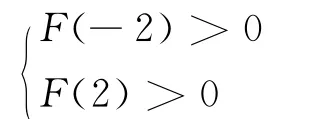
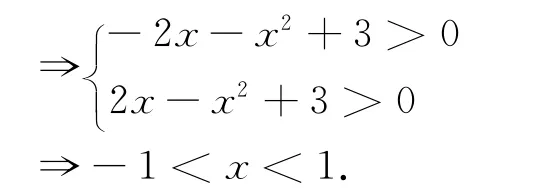
故当且仅当a=-1,b=1时,b-a取到最大值2.
猜你喜欢
中学数学教学(2023年5期)2023-10-30 06:12:40
语数外学习·高中版上旬(2022年2期)2022-04-09 13:56:12
音乐天地(音乐创作版)(2020年12期)2020-12-06 01:32:21
数理化解题研究(2020年19期)2020-07-22 08:10:14
人物画报(2019年2期)2019-09-10 07:46:47
读写算(2019年5期)2019-09-01 12:39:22
中学课程辅导·教学研究(2017年29期)2018-02-26 21:34:18
中华建设(2017年2期)2017-06-01 11:29:31
中学生数理化·高一版(2016年9期)2016-05-14 09:03:49
中学数学杂志(高中版)(2016年1期)2016-02-23 01:14:41

