高中向量教学的误区及其思考

江苏省丰县中学 曹 军 （邮编：221700）

向量进入高中数学教材已经好几年了.关于向量法，近几年数学期刊上的文章很多，但仔细品味所见诸例的解法，却不免困惑：解题过于注重代数形式，忽视几何性质，以致运用向量法解题时包含了大量的运算，自然较为繁琐.向量具有几何形式和代数形式的“双重身份”是将向量引入中学教材的一个重要原因.既然教材引入了向量法，所谓用人用其长处，那我们就要把向量的特点充分发挥出来，而不是穿新鞋走老路.笔者借此机会提供高三复习过程中处理的两个教学片断，供同行借鉴乃至有所启迪.

片断1 文［1］在第77页有：如图1所示，在平行四边形ABCD中，E是DC的中点，AE交BD于M，试用向量的方法证明：M是BD的一个三等分点.

教参和很多辅导书都给出了上述解法或者类似的解题思路.笔者的教学设计也是采用了上述解法.意料之外的是，看似简单常规的向量题目，却在教学过程中发生了不小的意外.

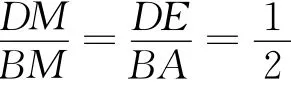
师：很好，简洁明快，但请你注意本题的要求是用向量法证明.

事实上，生1提供的方法比向量法更简洁、更容易理解.初中生很容易解决的题目，到了高中反而越来越复杂了.此刻，如何向学生解释向量法的先进性就显得尤为重要.否则，会给学生带来向量法不如综合几何法的数学印象，也极有可能扼杀学生探索向量的欲望.

师：能否利用向量法非常简单地证明此题呢？

学生都陷入深深的思考中.

师：我们知道，平面向量基本定理的重要前提是两向量e1、e2不共线，而结论有两点：一是存在一对实数λ1和λ2，使得a＝λ1e1＋λ2e2；二是这对实数是惟一的.这惟一性是说：a＝λ1e1＋λ2e2＝k1e1＋k2e2，则必有λ1＝k1，λ2＝k2.在解题中常常用到这个惟一性，看似新事物，但仔细一琢磨不过是向量共线概念的直接推论.事实上，因为（λ1－k1）e1＝（λ2－k2）e2，而e1和e2不共线，两端必然都是零向量，从而两端的系数都是0，必有λ1＝k1，λ2＝k2.如果简明一点可以这样说，若向量a和b共线且c和d共线，但a和c不共线，则从a＋c＝b＋d可推出a＝b和c＝d.这种由一个等式获取两个等式的法则，在解题中带来的好处是不言而喻的（如果是空间向量，则可以从一个等式获取三个等式）.联系这个结论你能解决此题吗？

要让学生掌握和熟练运用某个知识，教师就要有意识地给学生提供该知识应用的不同背景，学生只有在不同的背景中，形成了自觉运用该知识的“思维定势”时，才可以说是真正掌握了知识.为此，笔者又提供了一个问题，供学生思考.

如图2所示，在平行四边形ABCD中，AE⊥BD于E，CF⊥BD于F，求证：AE＝CF.

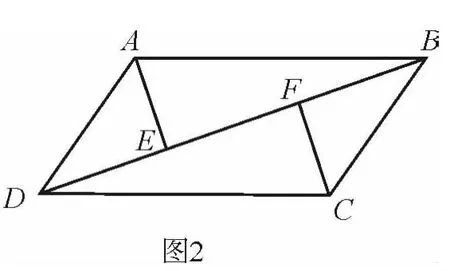
笔者认为引入向量法，首先要让中学老师能够感受到向量法的优势，而不是可有可无，更不是增加负担.单墫教授认为，同一个数学问题的不同解法，可以有美丑之分.简洁明快是一种数学美.在数学解题教学中，当然引导学生寻求更美的解题方法.解题及其教学应该从学生已有的知识基础和经验出发，跟着学生的感觉走，努力寻求自然的解法，这才是最真实和最宝贵的.因此，我们要寻找向量法解题的自然解法：用向量法处理涉及交点问题，其诀窍在于从一个涉及解题目标的向量等式出发，利用题设条件和向量等式代换，尽量把等式中的向量都转化到相交直线上，从而应用平面向量基本定理获取关键信息.心中只要有这个主见，绝大多数问题都能迎刃而解.所以，教学过程中，要让学生领略解题的核心方法，领略对数学的本质认识，领略对数学规律的理性认识.这些认识在活动中被反复利用，带有普遍的指导意义，是建立数学和用数学解决问题的指导思想.

以下方法在教学中比教普遍（此处省略教学的探索过程）：

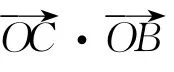
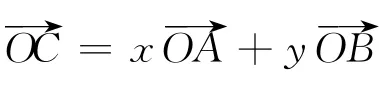
事实上，构造数量积、建立坐标系是向量问题代数化的常用方法，这种思维方式学生已经掌握.思路2对已知等式两边平方，实际上是两个向量自身作了一次“点乘”.此题如果固步于以上解题思维，未在此基础上再引导学生“探一探”，就会错失向量所具有的几何形式.

师：还有别的解题思路吗？

学生陷入了沉思.

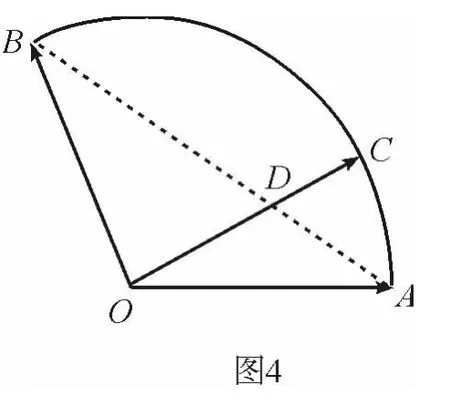
在笔者的启发下，同学们跃跃欲试.

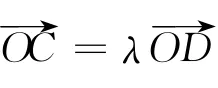
生5：老师，我从上述解答中似乎看到了一个定值，但还不确定.

师：你说说看（此时，笔者的心还是比较忐忑的，按照教学设计该问题已经结束，笔者无法预测接下来会出现什么状况.）.

师：此结论说明：当F在直线DE上的任意位置时，λ＋μ为定值t.你能联系这一结论解决此题吗？

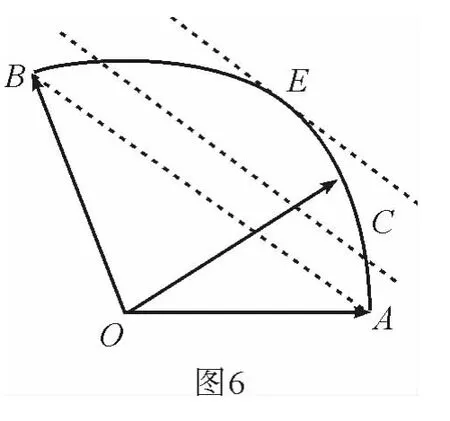
至此，学生们都对生5的独到见解给予肯定并给出热烈的掌声.

为使这种数形结合思想的应用更加深入人心，对它的应用规律的理性认识更加丰富深刻，笔者又创设了如下的问题情境，供学生思考：

从上面的两个教学片断来看，向量解题方法朝着更高的目标提升，还有很大的空间.同时，从这里也可看出，不是向量法本身有问题，而是没有正确使用向量法来解题.因此，在使用向量法解决问题的时候，无需死守套路，完全可以根据几何意义列出等式，计算与图形融为一体.关键在于领会向量几何，其运算不仅仅是数的运算，还包括图形的运算，这是向量法解题的特点.

基于以上两个教学片断，笔者认为有以下几点感悟：

第二，教师要注重阅读.叶澜教授说过：“课堂教学是一个动态生成的过程，再好的预设，也无法预知课堂教学中的全部细节.”课堂的立足点是学生，教学的思路应依照学生的思维和理解做出微调，只有这样，在课堂上才会“撞出”智慧的火花.扎实、深厚的专业知识是进行课堂微调的重要前提之一，而教师的专业知识的提高和阅读是分不开的.通过阅读，教师一方面可以接触数学的新思想、新思维、汲取先进的教育理念为我所用；另一方面可以提高自身的解题能力.如果笔者没有阅读过文［2］、文［3］的话，在面对片断1中生1的解答就不会“撞出”如此精彩的火花，而是平平淡淡的结束该问题的解答，与此同时也会挫伤学生学习数学的兴趣.因此，阅读对于教师而言至关重要.

第三，重视数学思想和方法的培养，给学生提供高质量的题目.中国有句古话说：“授人以鱼，不如授之以渔”，课堂上帮助学生掌握有效的学习方法和思维方法非常重要，教师要积极引导学生学会学习.若教师总想按照自己的思路走，生怕学生不符合标准答案，而常常越俎代庖，学生只能被牵着鼻子走，学生根本也没有从内心真正接受这些知识，想要再让他们能活用这些知识，就只能是一种奢望了.而数学思想和方法的培养少不了高质量的例题，按照波利亚的思想，要做一些“通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域”的题目.要集中力量于某几个真正有意义的问题，通过发掘问题的各个方面，从容不迫且彻底地讨论它们.

1 单墫等.普通高中数学课程标准实验教科书（必修）数学4［M］.南京：江苏教育出版社，2012

2 张景中，彭翕成.向量教学存在的问题及对策［J］.数学通报，2009（8）

3 张景中，彭翕成.绕来绕去的向量法［M］.北京：科学出版社，2010