条件式abc=a+b+c+2的几个等价式与应用
2013-09-24 01:14:16浙江省湖州市双林中学李建潮钱旭锋邮编313012
中学数学教学 2013年6期
浙江省湖州市双林中学 李建潮 钱旭锋 (邮编:313012)
本文谈谈条件式:
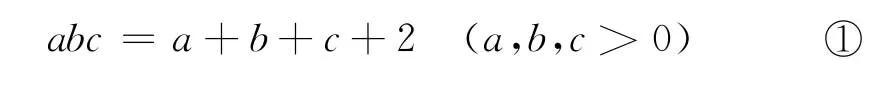
下的不等式证明题.
1 ①的等价式一与应用
①式等价于



上式两边都加2(bc+ca+ab),整理得
(a+b+c)(a+b+c+2)≥4(bc+ca+ab),
即(a+b+c)abc≥4(bc+ca+ab).
两边同除以abc,原不等式获证.

2 ①的等价式二与应用
①式又等价于

例2 已知正数a、b、c满足abc=a+b+c+2,求证:(a-1)(b-1)(c-1)≤1.
证明 已知条件等价于③式,且用反证法易知:bc、ca、ab>1.进而a、b、c三数中至少有两数大于1,不妨设a>1,b>1.
若c≤1,则求证式显然成立;
若c>1,则不等式(px-qy)2≥ (p2-q2)(x2-y2)(p、q、x、y∈R)应用于 ③ 式,有


联立例1,可获:
结论1 已知正数a、b、c满足abc=a+b+c+2,则
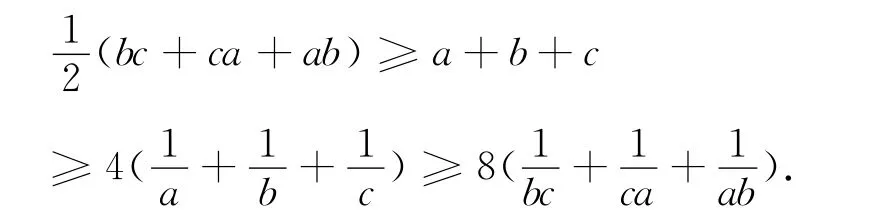
3 ①的等价式三与应用
①式等价变形为:

这就是①式的第三个等价式,它与如下赛题“连通”:
赛题 (第20届伊朗奥赛题)已知正数a、b、c满足a2+b2+c2+abc=4求证:
a+b+c≤3.

结论2 已知正数a、b、c满足

(或 ④ 或 ① 或 ③),则
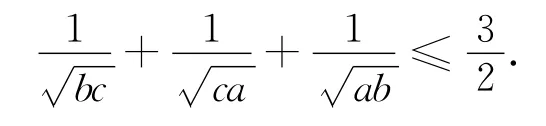
(1998年日本IMO选拔赛题的加强)
下面举二例以示应用:

证明 已知条件等价于

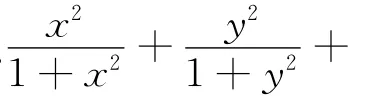
例4 (2004年上海竞赛题)若α、β、γ∈ (0,),sin2α+sin2β+sin2γ=1,求证:


应用结论2,得

由此易证(cotαcotβcotγ)2≥8;进而由均值不等式,可证cotα+cotβ+cotγ≥ 3.
类似 若α、β、γ∈ (0,),cos2α+cos2β+cos2γ=1,求证:

猜你喜欢
中等数学(2022年7期)2022-10-24 01:47:20
中等数学(2022年4期)2022-08-29 06:27:14
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30 06:36:10
中等数学(2020年7期)2020-11-26 08:03:46
中等数学(2020年4期)2020-08-24 08:08:38
中等数学(2019年5期)2019-08-30 03:52:22
中央民族大学学报(自然科学版)(2018年1期)2018-06-27 01:27:40
中学生数理化·高一版(2017年9期)2017-12-19 12:15:14
高中生·天天向上(2017年4期)2017-06-09 02:27:50
中学生理科应试(2017年2期)2017-04-01 21:03:31

