同伦法部分极点配置中特征灵敏度计算
吴晶莹,王冠楠
(浙江大学 电气工程学院,浙江 杭州 310027)
0 引 言
随着电力事业的蓬勃发展,电力系统规模不断扩大,电力网络日益复杂,电网运行越来越容易接近稳定极限。使得低频振荡现象屡屡发生,严重时会引起停电事故,给经济造成了巨大的损失也给社会安定带来了不良的影响[1-2]。因此,分析电力系统低频振荡及其抑制措施具有非常重要的现实意义。阻尼是影响低频振荡的关键,安装电力系统稳定器(Power System Stabilizer,PSS)作为一种经济有效的阻尼抑制方法得到了广泛的应用。而如何合理配置、选定电力系统稳定器参数是备受关注的问题[3-4]。
极点配置作为PSS参数配置的常用方法已经被广泛使用,文献[5]采用全部特征值,虽然鲁棒性好,但对于大系统常常会出现所谓“维数灾”的问题。文献[6-8]分别利用选择模式分析法、AESOPS法、S矩阵法,以确保计算精度和速度都可以满足大电力系统的要求,但计算结果受到搜索初值和范围的影响很大,不能保证所有的负阻尼和弱阻尼模式都被搜索到。另外牛顿法[9],初值的依赖性非常强,而对初值求解往往很复杂。文献[10]验证了最小二乘同伦法的可行性,以及它的收敛速度和鲁棒性都比经典的牛顿法好很多。
目前在电力系统研究领域中对于特征灵敏度研究虽有不少,却多为针对特征值灵敏度的分析,对于特征向量及其在电力系统的计算分析却很少见,传统的特征向量灵敏度的计算方法如文献[11]中所述需要知道所有的特征向量才能求取特征向量灵敏度并且仅适用于只有一些特征向量的小系统,不适用于大系统。文献[12]提出了特征灵敏度分析方法,但是又由于负荷矩阵的稀疏性或者数值不稳定,对实际系统的分析并不可行。
本研究提出一种基于最小方差全概率同伦法的极点配置方法,以PSS可调参数为优化变量,以部分极点配置为目标,通过利用多种特征向量灵敏度分析方法实现小干扰下PSS的参数优化配置,并且着重分析特征灵敏度在其中的计算,分析多种特征值灵敏度、特征向量灵敏度的计算方法,利用经典的3机9节点系统和New England10机39节点系统算例分析该方法的可行性。
1 小信号稳定及简单的PSS模型
根据数学模型的不同类型[13],电力系统小干扰稳定性分析的方法可以分为4类:数值仿真法、特征值分析法、频域分析法和非线性理论分析法[14]。而特征值分析法是一种成熟的小干扰稳定研究方法,也是公认非常有效的分析方法,它以线性系统和李雅谱诺夫第一定律为基础,将系统在平衡点线性化,形成状态方程矩阵,计算特征值、特征向量、参与因子等信息。
PSS是抑制低频振荡最简单有效的方法,本研究中PSS调试的是单机无穷大系统。通过配置多个标准的二阶电力系统稳定器模型实现,示意图如图1所示。

图1 标准的二阶电力系统稳定器
其传递函数为:
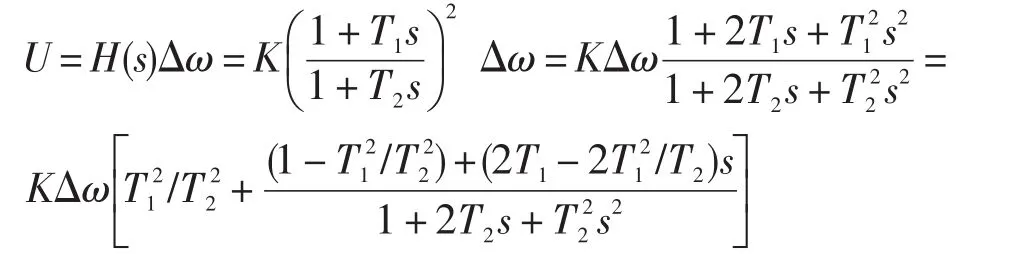
设PSS的状态变量为:
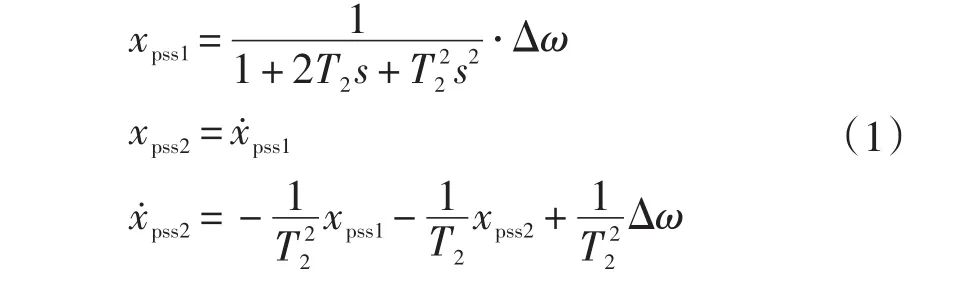
综合以上结果,制定一个PSS状态方程,输入Δω为:

闭环系统的状态矩阵及其系数的偏导为:
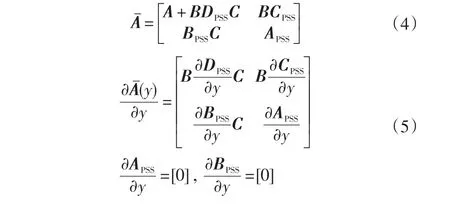
2 最小方差同伦法极点配置
研究者设计PSS参数的时候,对于控制反馈环节,将系统中不符合稳定运行条件的极点重新配置到复平面内合理的位置,使得新的系统符合动态稳定标准,振荡得以被抑制。
又因为知道闭环系统可以表示为式(4),在传统方法中,极点配置问题可以认为是求解目标函数方程:
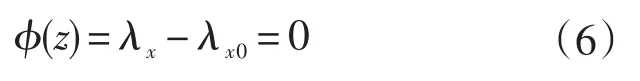
然而,目标函数方程并不一定有解,为了增加极点配置问题的可解性,引入最小方差极点配置,它具有如下的特点:无需使用泰勒法展开非线性模型,理论严密,特别适合求解非线性强度较高的模型;对初值依赖性极低,具有大范围收敛性,数值解稳定,且精度高。它的目的是让目标解与目标值的距离的平方和最小[15]:
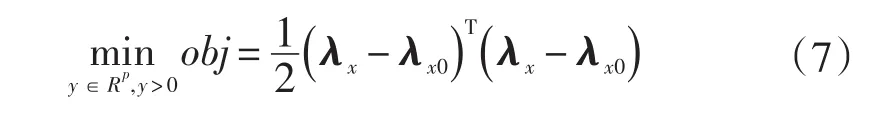
相当于上式满足:
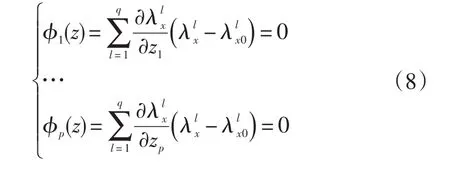
下面引入同伦法的概念,它作为代数拓扑学(To⁃pology)的基本概念,来源于延拓法,通过对不稳定的最优化问题添加一个稳定泛函,把它变为一个稳定的最优化问题[16]。自19世纪初开始作为数值工具用于求解一般的非线性方程组,至今已取得了卓越的成果。具体的求解过程如下,设有一个非线性方程组:

设z1,z2为p维空间Rp的非空子集,ϕ:z1→z2为一个光滑的同伦映射。在同伦算法中,并不是直接求解式(9),而是在其中加入一个已知其解或者易于求解的方程φ(z),配合同伦参数,构造同伦方程:
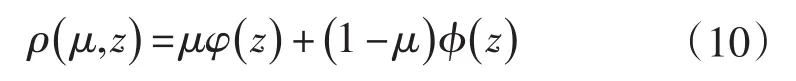
其中,μ∈[0,1],ρ(μ,z)为同伦函数,且本研究采用的是全概率同伦法,即概率为1,‖μ˙,z˙‖2=1,即同伦方程具有以下关系:
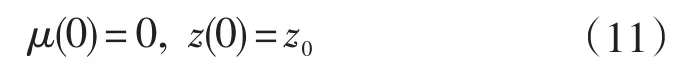
利用参考文献[17]中所用的方法,求解如下:
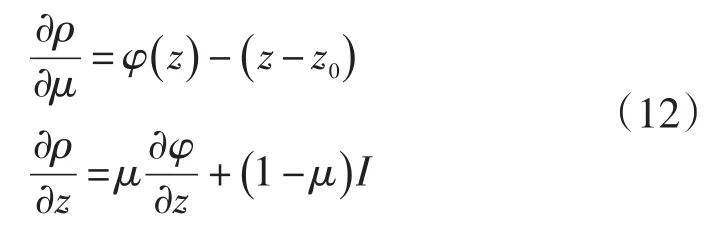
为了利用同伦算法还需要知道φ(z)的雅可比矩阵如下所示(其求解过程将在下文中详细叙述):

3 特征灵敏度的分析
由公式可以知道,需要求解同伦算法需要知道特征值一阶灵敏度、特征值二阶灵敏度、特征向量灵敏度,具体的求解过程将在下文详述。
3.1 特征值一阶灵敏度
对于系统的状态矩阵A有以下方程:
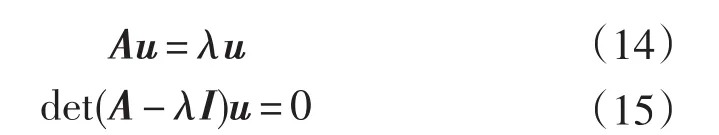
式中:λ—A的特征值,λ=[λ1,λ2,...,λn];u—右特征向量;v—左特征向量。
用viTui=Ci=1进行标准化,来求解特征值一阶灵敏度∂λ/∂zi,将式(14)关于zi求导,可得:

再对上式两边都左乘vi,整理可得:

3.2 特征值二阶灵敏度
除了需要求解特征值的一阶灵敏度,还需要求解特征值的二阶灵敏度。将上式关于zj求导,可得:
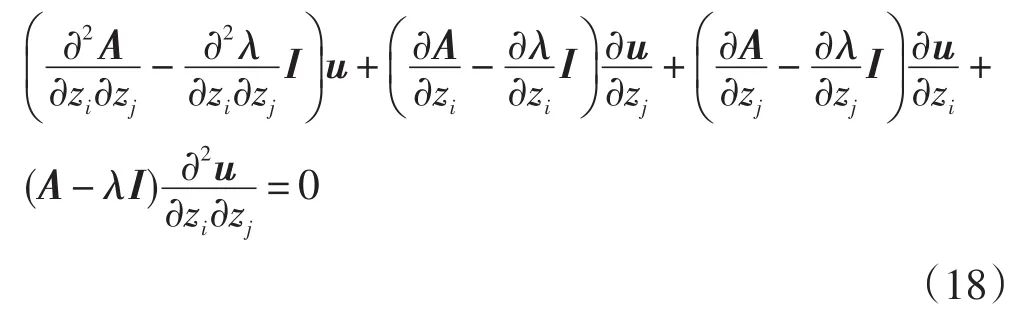
将上式的左右两边都乘以vT,化简可得:
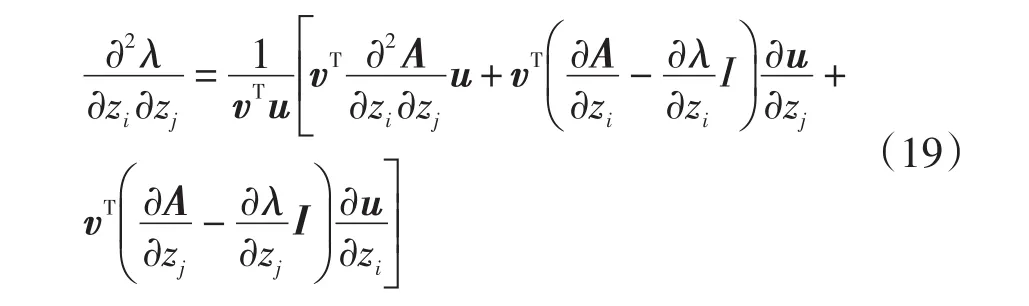
为了求解二阶特征值灵敏度需要知道:第i个特征值的左右特征向量v,u;第i个特征值关于参数zi,zj的一阶特征值灵敏度;状态矩阵的二阶偏导数;特征向量关于参数zi,zj的一阶特征值灵敏度。
这表示要求解特征值的一阶、二阶灵敏度,并不需要求解状态矩阵的所有特征值。
3.3 特征向量灵敏度
特征灵敏度的计算主要是指特征值和特征向量导数的数值计算。特征值导数的计算比较容易,困难在于特征向量导数的计算。由上可知,为了求解特征值二阶灵敏度,其中最关键的就是会求解右特征向量一阶灵敏度。常见的计算方法主要可以分为以下5种[18]:①差分法;②模态法;③NELSON类方法;④代数法;⑤迭代法。
其中,差分法和迭代法又属于数值法,而NELSON法、模态法属于解析法。由于大部分特征灵敏度的研究是集中在机械、土木、航空、航天等方面,研究的系统大多数为对称无阻尼系统,而小干扰稳定运行的环境是实非对称系统,所以其中的大量方法并不可行,下面本研究选择了切实可行且具有代表性的几种算法对特征向量灵敏进行求取:
3.3.1 FOX和KAPOOR的方法
1968年FOX和KAPOOR[19]首先提出了特征值导数和特征向量的求解方法,利用完整的模态展开法,对对称无阻尼系统给出了特征值和特征向量一阶导数的精确求解。该方法指出:将式(14)的两边进行求导,可得:
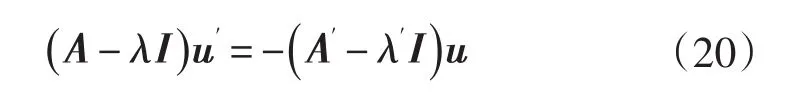

当方程具有n个互不相同的特征值时,(A-λI)为奇异阵,秩为n-1,此时特征向量灵敏度可以由下式所求:

由此可见,利用经典的模态展开法来进行特征向量灵敏度的求解,需要知道所有的特征值、特征向量,对于维数大的向量系统而言是一个异常复杂的过程。
3.3.2 John Condren的方法
在文献[20]中,John Condren提出了一种求解特征向量灵敏度的方法,因为:
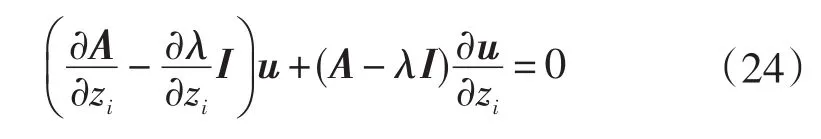
其中:A-λI是奇异的,所以无法在式子两边直接左乘(A-λI)-1来求解特征向量灵敏度。因此本研究提出了一种标准化条件:

所以研究者可以构造方程,利用标准化方程来分别求解特征向量一阶灵敏度的实部和虚部:
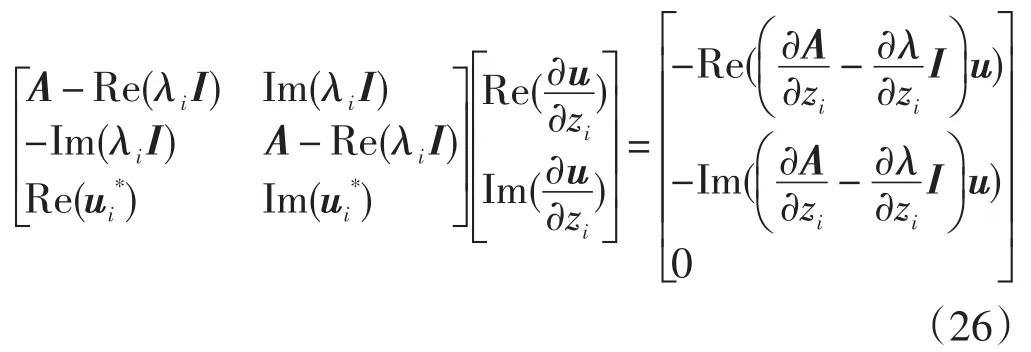
使用该方法时,只要知道需要配置的特征值以及它所对应左、右特征向量即可。
3.3.3 M.jankovic的方法
另一种方法利用文献[21]中所提的新的约束条件,首先将下式:
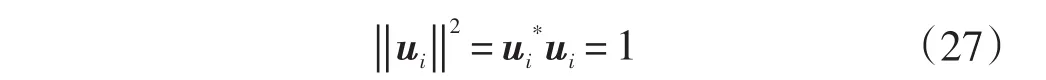
关于zi求偏导,可以得到:
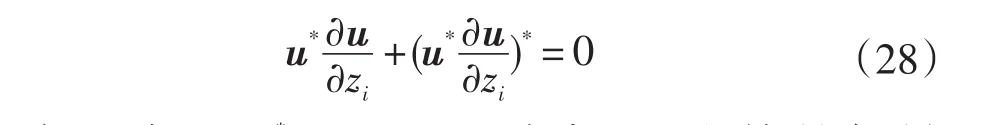
方程在 Im[u*(∂u/∂zi)]=0 时成立,也就是如果u*(∂u/∂zi)是实数,那么上式u*(∂u/∂zi)+[u*(∂u/∂zi)]*=0 成立,可以变为:
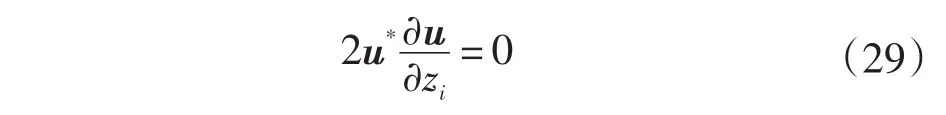
若u*∂u/∂zi=0 两边左乘u,可以得到:
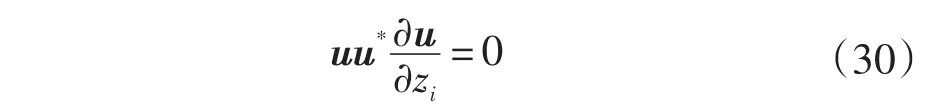
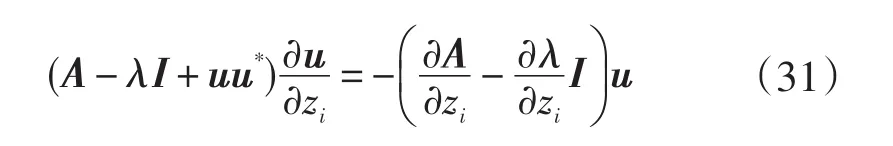
同样也可以利用上式展开分别求解特征向量的实部和虚部获得所求解。3.3.2节中的方法和3.3.3节中的方法主要区别是利用不同的归一化条件进行运算分析。
3.3.4 NELSON的方法
以NELSON[22]为代表的一系列方法都称为直接法,它就是直接处理特征值向量导数在控制方程中系统矩阵的奇异性。其基本思想是把特征向量导数表示为齐次方程的通解和非齐次方程的特解的和的形式,再对两部分分别求解,假设:

联立可得:
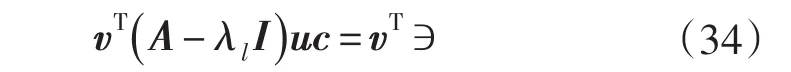
又因为vTAu=diag(λ),那么方程等于:
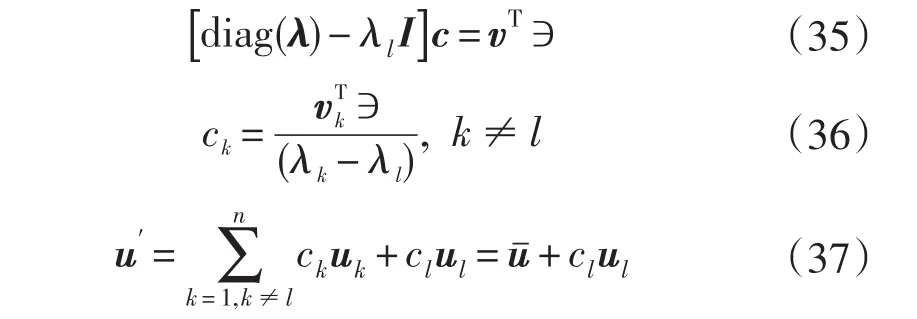
uT*u=1,取偏导,得:

将式(37)代入,可以求得:

求解u′的关键是求解uˉ,考虑齐次方程:
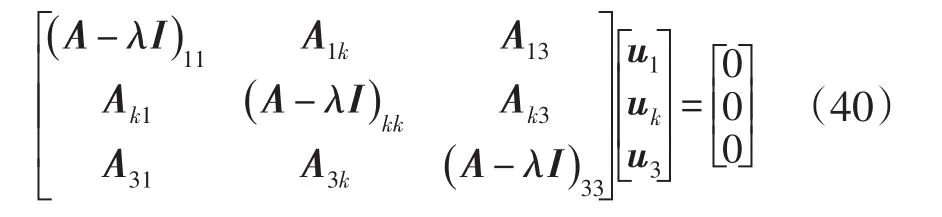
也可以表示成:
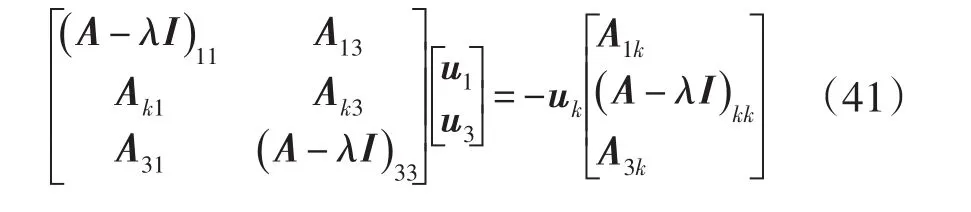
如果uk≠0,那么 (A-λI)的第k列,是剩下(n-1)列的线性组合。同理可得,对于左特征向量v:
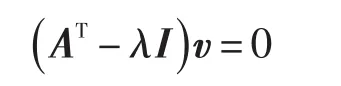
如果vk≠0,那么(AT-λI)的第k列是(A-λI)剩下的(n-1)行的线性组合。综上所述,可得如果vk≠0,uk≠0,那么(A-λI)的第k行第k列都可以删除,则u1,u3满足:

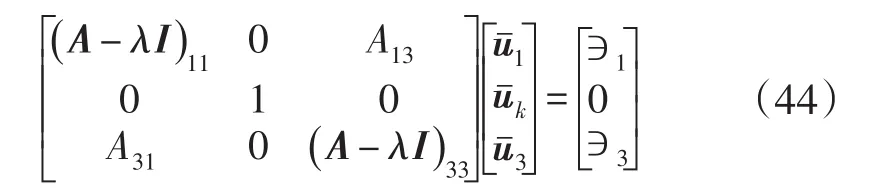
综上所述,第i个特征值所对应的特征值向量灵敏度可以表示为:
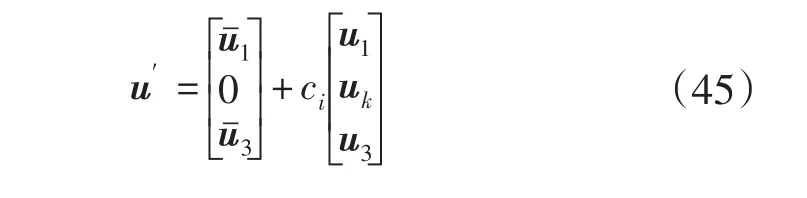
这样就得到了u′,然后利用LU分解法来求解PSS超前滞后环节的参数。
NELSON计算的优点是不用求解每一个特征值,只要求解需要的特征值即可,保持了结构特征值问题的对称性和带宽特点,但在求解重根特征值时有局限性。
4 算法实现
算法实现过程如下:
(1)初始化系统参数;
(2)求取系统的闭环状态矩阵A;
(3)求取特征值以及相应的左、右特征向量λ,v,u;
(4)求取特征向量灵敏度∂u/∂zi;
(5)利用最小方差同伦法求∂ρ/∂zi;
(6)利用改进欧拉法求得μ,zi;
(7)得到配置后的极点以及PSS参数;
(8)判断结果是否提高了阻尼、降低了振荡频率。
运算流程图如图2所示。
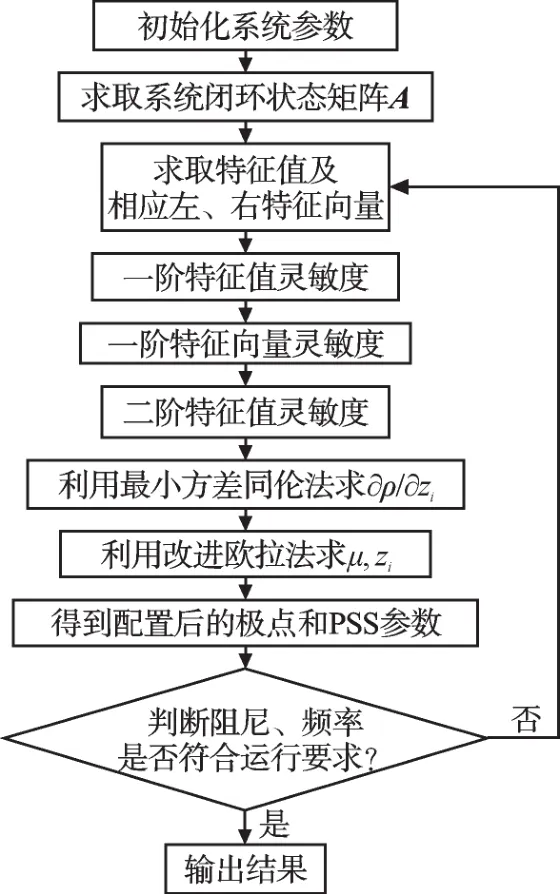
图2 运算流程图
5 算 例
5.1 3机9节点算例
为了进一步验证上述同伦求解极点配置的方法是有效的,本研究引入的3机9节点系统如图3所示,该系统是一个经典的小信号稳定分析系统,它有3台发电机、3个负荷、9条输电线路。
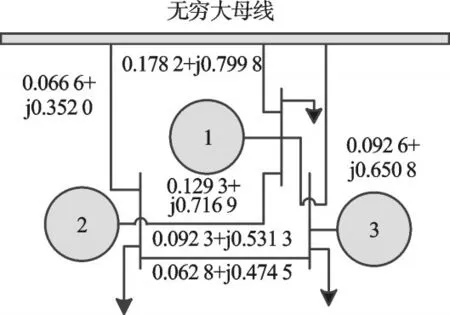
图3 系统接线图
3.3.1 节中的方法在运算速度上已经非常缓慢,下面本研究使用3.3.2节、3.3.3节、3.3.4节中的方法分别进行极点配置,将系统的特征值配置到目标极点的位置,初始Ta=[0.16,0.19,0.165];K=[44.5,83.5,25.50],如图4所示。
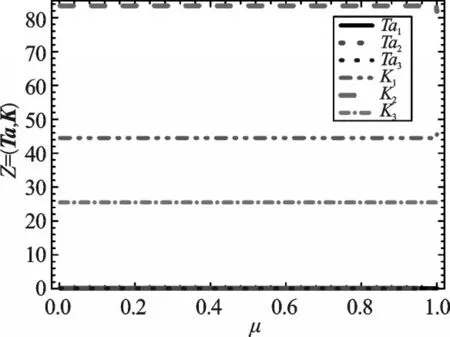
图4 Ta和K随着μ变化到1的变化
随着特征值λ1-λ6达到想要配置的点,参数Ta、K的变化过程如图5所示,最终在μ=1的时候停止,是一个全概率的过程。以及在这个过程中,特征值λ1-λ6也都被配置到了目标位置。此时参数Ta=[0.164,0.194,0.169],K=[44.119,83.956,25.504],λ=[-3.997,-3.617,-1.899,-8.364,-10.984,-13.689]。
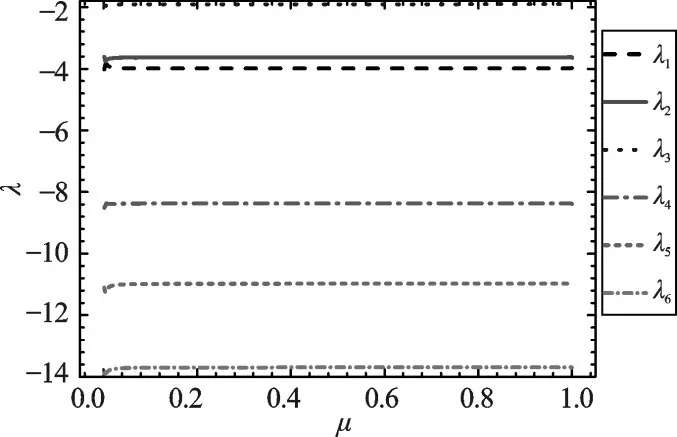
图5 λ1-λ6随着 μ变化到1的变化
5.2 New England 10机39节点算例
同时针对New England 10机39节点的系统算例,本研究分别使用上述几种方法对其进行计算,初始Ta和K为:Ta=[0.250 65,0.250 88,0.269 38],K=[25,25,25.000 16],采用3.2.2节方法时却发现由于rank=n-1,3.3.2节方法产生的最优解具有数值错误,而3.3.3节、3.3.4节方法仍然适用,配置结果如图6、图7所示。
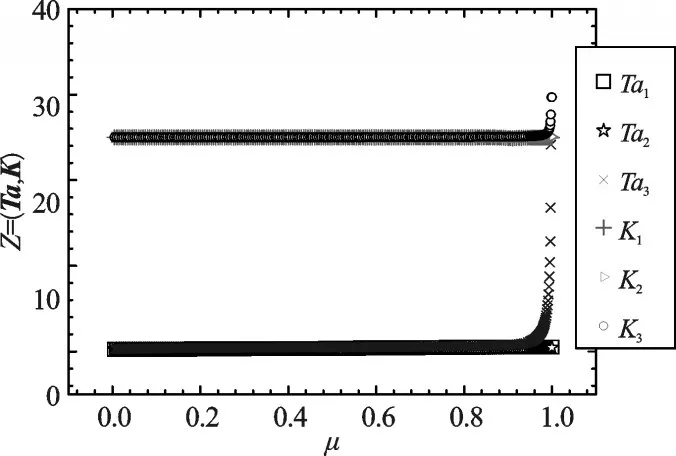
图6 Ta和K随着 μ变化到1的变化
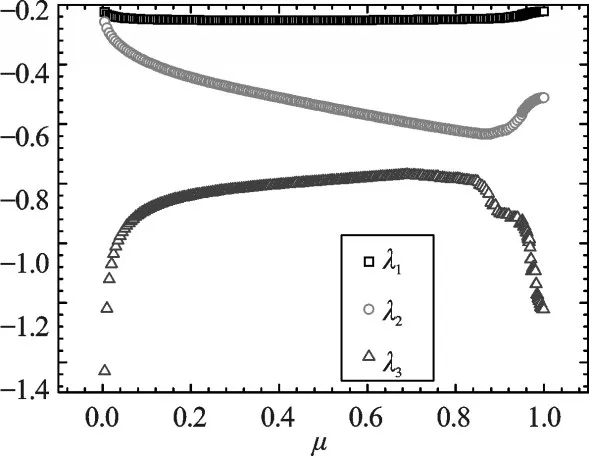
图7 λ1-λ3随着 μ变化到1的变化
可以看到通过3.3.2节、3.3.3节、3.3.4节方法,都能够将特征值配置到目标位置,但是相比3.3.4节方法,3.3.2节、3.3.3节方法虽然计算过程简单,但是在求解大系统的时候会出现不稳定,求解矩阵奇异,稀疏性较差,无法求得精确解。3.3.4节方法具有更好的鲁棒性。
6 结束语
本研究介绍了特征灵敏度在同伦最小方差极点配置中的计算,其中对于特征向量灵敏度分别提出了3种计算方法,通过对算例的比较分析验证了3.3.2节方法和3.3.3节方法的可行性,但它们稀疏性较差且大系统时矩阵会出现病态,3.3.4节方法具有更好的适用性、鲁棒性以及特征灵敏度计算方法的可行性和有效性。
(References):
[1]朱 方,赵红光,刘增煌,等.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报,2007,27(1):1-7.
[2]余贻鑫,李 鹏.大区电网弱互联对互联系统阻尼和动态稳定性的影响[J].中国电机工程学报,2005,25(11):6-11.
[3]王 康,金宇清,甘德强,等.电力系统小信号稳定分析与控制综述[J].电力自动化设备,2009,29(5):10-19.
[4]韩祯祥,薛禹胜,张伯明.1996年国际大电网会议(CI⁃GRE)第37,38,39组简介[J].电力系统自动化,1997,21(1):45-48.
[5]袁 野,程 林,孙元章.采用广域测量信号的 2级 PSS控制策略[J].电力系统自动化,2007,30(24):11-16.
[6]ROUCO L,PEREZ-ARRIAGA I J.Multi-area analysis of small signal stability in large electric power systems by SMA[J].Power Systems,IEEE Transactions on,1993,8(3):1257-1265.
[7]SAUER P W,RAJAGOPALAN C,PAI M A.An explana⁃tion and generalization of the AESOPS and PEALS algo⁃rithms[power system models][J].Power Systems,IEEE Transactions on,1991,6(1):293-299.
[8]UCHIDA N,NAGAO T.A new eigen-analysis method of steady-state stability studies for large power systems:< e1>S</e1> matrix method[J].Power Systems,IEEE Transac⁃tions on,1988,3(2):706-714.
[9]ANGELIDIS G,SEMLYEN A.Improved methodologies for the calculation of critical eigenvalues in small signal stabili⁃ty analysis.Power Systems[J].Power Systems,IEEE Transactions on,1996,11(3):1209-1217.
[10]WANG Guan-nan.A Probability-one Homotopy Method for Partial Pole Assignmen[tC].CEPSI 2012.Bali,2012.
[11]WANG K W,CHUNG C Y,TSE C,et al.Multimachine ei⁃genvalue sensitivities of power system parameters[J].Pow⁃er Systems,IEEE Transactions on,2000,15(2):741-747.
[12]NAM H K,KIM Y K,SHIM K S,et al.A new eigen-sensi⁃tivity theory of augmented matrix and its applications to power system stability analysis[J].Power Systems,IEEE Transactions on,2000,15(1):363-369.
[13]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析/现代电力系统丛书[M].北京:清华大学出版社,2002.
[14]仲悟之.大型电力系统小干扰稳定性分析方法研究和软件开发[D].北京:中国电力科学研究院,2005.
[15]NOCEDAL J,WRIGHT S J.Numerical optimization[M].Springer verlag,1999.
[16]TIKHONOV A N,ARSENIN V Y.Solutions of Ш-posed Problems[M].VH Winston&Sons,Washington,DC,1977.
[17]唐利民,朱建军.不适定非线性最小二乘问题的正则化同伦法及其应用[J].大地测量与地球动力学,2010,30(6):51-56.
[18]徐忠海.结构特征灵敏度分析若干问题研究[D].长春:吉林大学,2008.
[19]FOX R L,KAPOOR M P.Rate of change of eigenvectors and eigenvalues[J].AIAA Journal,1968,12(6):2426-2429.
[20]CONDREN J,GEDRA T W.Expected-security-cost opti⁃mal power flow with small-signal stability constraints[J].Power Systems,IEEE Transactions on,2006,21(4):1736-1743.
[21]JANKOVIC M S.Exact nth derivatives of eigenvalues and eigenvectors[J].Journal of guidance,control,and dy⁃namics,1994,17(1):834-837.
[22]NELSON R B.Simplified calculation of eigenvector deriva⁃tives[J].AIAA Journal,2011,14(9):823-832.

