喷墨印花纹理图像的期望最大化聚类分割算法*

周佳男，冯志林，朱向军

（1.浙江商业职业技术学院 信息技术学院，浙江 杭州 310053；2.浙江工业大学 之江学院，浙江 杭州 310024）

0 引 言

喷墨印花纹理是一种细致型纹理，特点是微小、稠密，其纹理图像的灰度级相对较集中。喷墨印花纹理的一项重要特征是其不规则性，它不是由统一固定的模式严格有序地排列而成，而是由随机分布的花纹构成的［1］。喷墨印花纹理图像分割是将纹理图像分成各具特性的区域并提取出感兴趣的纹理目标的技术和过程。

近年来在图像分割领域不断出现很多新的研究成果，其中将聚类算法应用到图像分割领域中，可以有效地提高图像分割的精度，是一种较新的研究方法。聚类算法又称为无监督学习算法，目前被用于图像分割的常见聚类算法主要有K均值［2-3］和谱聚类［4-5］等。聚类分割算法是将图像区域划分成若干个不相交的分块集合，在聚类的过程中以及最终的输出结果中均只将分块模式划分到隶属度最大的聚类中。由于传统聚类分割算法在聚类过程中对图像噪声敏感，且没有考虑纹理图像的空间特性，其对含噪喷墨印花纹理图像的分割结果精度较差。

本研究提出一种基于分块标定和期望最大化相结合的聚类分割算法。该算法首先对纹理图像建立表征空间特性的自回归模型，并对图像数据进行分块，使得交叠的分块窗口集能够覆盖整个图像；然后，利用自回归模型满足多元高斯分布的特性，设计出一种利用分块标定策略的期望最大化算法来稳健估计自回归模型中混合分布的参数；最后采用分块聚类优化技术，通过聚类合并的迭代过程，获得纹理类的个数和分块集，最终得到纹理图像的块状聚类分割图。

1 自回归纹理图像模型

近年来，国内外学者采用自回归模型建立图像的纹理分布模型［6-7］，并通过邻域系统建立相邻像素间的相互作用关系。建立自回归纹理图像模型的目标是为了获取纹理图像在局部尺度上的特征集。由于二维自回归模型可以实施最大似然参数的线性估计，本研究采用该模型对纹理图像进行建模。

设图像X包含K个纹理类，k是序标，第k个纹理类的自回归模型表述为:

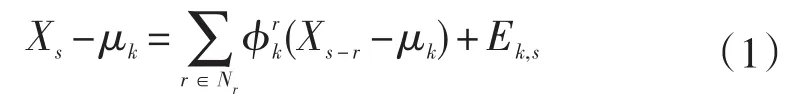
式中:Xs—M×M区域上点s=(x,y)处的灰度值，且1≤x,y≤M；Nr—点s的4邻域，非对称自回归系数—区域灰度均值；零均值、协方差为Σk的独立多元高斯随机场。

由式（1）可知，图像X的参数θ={θk|k=1,...,K}，其中θk={μk,ϕk,Σk}是第k个纹理类的参数。

由于式（1）中的观测数据X在获取过程中受到噪声污染，自回归模型（1）的θ参数估计属于“不完整数据”的参数估计问题。期望最大化（EM）算法可以从“不完整数据”中对参数进行极大似然估计（MLE），是解决包含非完整数据的统计估计问题的一个有效的工具，已在图像处理、数据拟合、目标跟踪等领域得到广泛应用［8-9］。

EM算法是一种通用的最大似然参数估计方法，它的一个重要用途是实现混合概率密度函数的参数估计问题。因此，本研究采用EM算法进行纹理图像自回归模型的参数估计。

2 参数估计算法

EM算法每一次迭代由两步组成:E步和M步。E步就是在给定数据集和当前参数估计的情况下，求完整数据集似然函数对数变换的期望值；M步就是使E步得到的期望值最大化。EM算法通过E步和M步的不断迭代，逐步改进模型的参数，直至满足收敛条件为止，这样就可以使模型的参数逐渐逼近真实参数，从而得到待求参数的最大似然估计值。

由于式（1）是建立在区域邻域系统上的，很多学者采用分块标定算法来对其进行参数估计。文献［10］将分块标定算法应用到不完整数据的参数估计中，有效提高了参数估计的效果。本研究采用分块标定算法将整幅图像等分成多个小块，再在每个小块中根据纹理特征进行标定，在邻域内用匹配度最大分块的类标号作为当前块集类标号，然后采用伪采样过程，对参数估计的过程进行更新，提高参数估计的精度。

具体地，本研究将分块标定算法和EM算法相结合，在EM算法中加入分块标定的步骤，提出一种改进的期望最大化算法（block-labeling EM，BLEM）。BLEM算法在E步后引入分块标定L步，该步骤将根据当前后验分布的值进行Gibbs采样，进行标签标定；同时根据采样所得的先验概率，对自回归模型系数进行估计。在M步中则利用L步生成的先验分布进行参数更新。

设Ak是属于纹理类k的块集，Wk=|Ak|是块集的个数，本研究提出的BLEM算法设计如下:

STEP1 设置迭代序标l=0，迭代阈值L，收敛误差阈值Mε，θj的初始后验概率P(l)(Ak|θj)=1/K，j=1,..,W。

STEP2 E步

STEP2.1 对每一个θj，确定后验概率值:

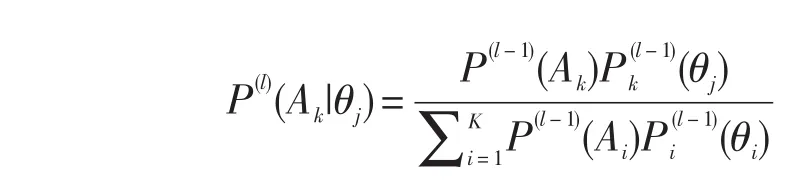
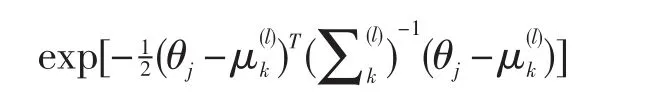
STEP2.2l←l+1，如果l＜L-1，则转至STEP3，否则转至STEP4.2。

STEP3 L步

STEP3.1 计算E步所得后验分布的期望值Q(P(l)(Ak|θj))，并利用其为θj设置聚类标签k；

STEP3.2 利用Gibbs采样技术，得到块集Ak的先验概率分布P(l)(Ak)，并估计自回归系数ϕk。

STEP4 M步

STEP4.1 利用L步产生聚类分块Ak，更新聚类分块的均值向量和协方差向量

STEP4.2 计算收敛误差值ε，如果ε＜Mε，则转至STEP1，否则转至STEP5。

STEP5 算法结束，并输出θk。

3 分块聚类分割算法

本研究提出的分块聚类分割算法（block cluster segmentation algorithm，BCSA）属于无监督算法，因此，其对图像X的分割过程主要包括:

（1）估计纹理模型的参数θ；

（2）估计纹理类的个数K；

（3）获取纹理类的分块集{Ak|k=1,..,K}。

BCSA算法的第一个过程由BLEM算法完成，因此，下面研究BCSA算法对后两个过程的实现。

由于参数θk已由BLEM算法估计得到，图像块XAk关于θk的条件概率为:

由于Wk=|Ak|是满足多项式分布的随机变量（参数为ρk），则图像X和Ak关于θ和ρ的条件概率为:

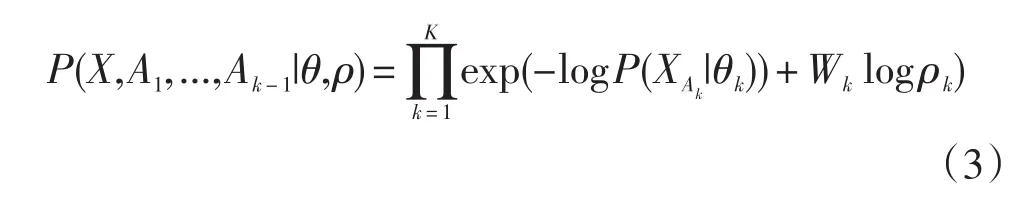
由式（3）可知，BCSA算法的后两个过程可通过贝叶斯优化式（3）实现。由于式（3）同时包含了4个未知参数K、A、θ和ρ，本研究采取固定部分参数的策略进行求解。

综上所述，本研究提出的分块聚类分割算法BC⁃SA设计如下:

STEP1 输入原始图像，设置聚类类别数K，并将其作为纹理类个数的初始值；

STEP2K和{Ak}固定。采用BLEM算法求解θk，获得块集Ak的统计特征，计算ρk的似然估计值ρ^k=Wk/W；

STEP3K和{θk,ρk}固定。该步骤将对块集Ak重新划分，为此，本研究将图像X的整个区域S划分成若干分块集Zw，即有S={Zw|w=1,...,W}。利用观测数据为每个分块选择最匹配的纹理，并得到新的块集估计值:

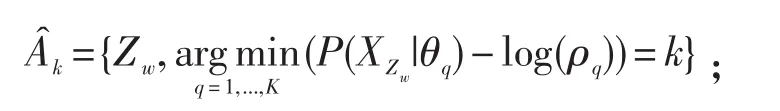
STEP4 减少聚类中心个数K的值，并通过最近邻匹配策略，迭代合并相邻聚类区域；

STEP5 检测聚类中心个数是否无变化，如果变化，则转至STEP2，否则转至STEP6；

STEP6 算法结束，并输出图像聚类分割图。

4 实 验

为了验证本研究算法的有效性，笔者将其用于喷墨印花纹理图像分割。本研究采用一幅大小为256×256的喷墨印花纹理图像进行分割实验。本研究算法的参数设置为:迭代阈值L=1 000，收敛误差阈值Mε=0.001，纹理类个数初始值K=10。

采用本研究算法所得的图像分割结果如图1所示。原始图像如图 1（a）所示，迭代200，400，600和800次后所得聚类图如图1（b～e）所示，分割图如图1（f）所示，C1～C5是聚类分割所得的纹理类。由图1（b～e）可以看出，本研究算法在迭代过程中，通过分块标定和聚类合并的过程实现了对不同纹理类的区域聚类。随着迭代次数的不断增加，分割目标与背景的灰度重叠情况得到不断改善，重叠部分的分块区域会逐渐往各自的聚类中心合并，最终达到分块区域隔离的目的。由图1（f）可以看出，本研究算法不仅可以完成图像前景和背景的分离，同时还可以实现前景区域中不同纹理类区域的边界划分，从而得到不同纹理类的图像分割结果。

图1 本研究算法所得分割结果

本研究算法在迭代800次时，纹理类C1～C5在进行自回归模型求解时的参数值列表如表1所示。

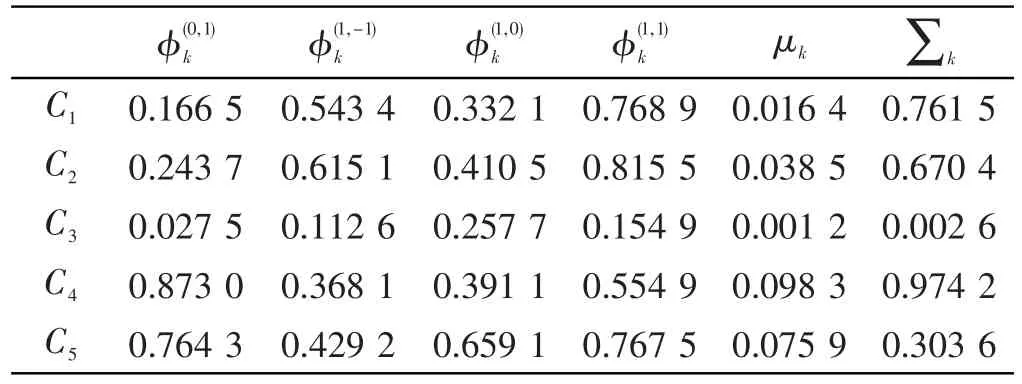
表1 纹理类C1～C5迭代800次时的参数值列表

最后笔者对含噪图像（噪声尺度σ=30）的分割情况进行验证，并将本研究算法（迭代800次）与文献［2］中的经典K-Mean聚类分割算法（CHEN算法）进行比较。从图2可以看出，本研究方法能准确地将前景目标和背景区域分离，且分割结果优于CHEN算法，尤其是在图2（a）的方形区域，本研究方法能将该区域分割开来，而CHEN算法产生了严重的错分，不能进行正确的分割。

实验结果表明，本研究算法对于纹理图像在噪声环境下的区域一致性和分割准确性均好于CHEN算法，对噪声具有更好的鲁棒性。

图2 本研究算法与CHEN算法比较

5 结束语

为了提升现有聚类算法对含噪喷墨印花纹理图像分割效果不足的缺陷，本研究对聚类算法进行改进，提出一种基于分块标定和期望最大化相结合的聚类分割算法。为了提高聚类分割算法对噪声的鲁棒性，本研究算法采用分块标定策略的期望最大化算法来估计自回归模型中混合分布的参数。同时，本研究算法采用分块聚类优化技术，通过聚类合并的迭代过程，获得纹理类的个数和分块集，并得到最终的聚类分割结果。

实验结果表明，本研究算法能够有效克服现有聚类方法对噪声敏感的缺点，具有较强的抗噪性。同时本研究算法能够准确定位花纹形状的聚类边界，具有较高的分割精度，这些特点对喷墨印花纹理图像的分割研究具有重要的意义。

（References）:

［1］YANG X H，SUI J H，MENG B，et al.Auto-generating uni⁃form stochastic Web images for ink-jet printing textiles［J］.Textile Research Journal，2010，80（18）:1942-1948.

［2］CHEN C W，LUO J，PARKER K J.Image segmentation via adaptive k-mean clustering and knowledge-based morpho⁃logical operations with biomedical applications［J］.IEEE Transactionson ImageProcessing，1998，7（12）:1673-1683.

［3］王静雷，厉小润.基于Kmeans和图像熵聚类的热红外目标检测算法［J］.机电工程，2012，29（12）:1490-1493.

［4］周 林，平西建，徐 森，等.基于谱聚类的聚类集成算法［J］.自动化学报，2012，38（8）:1335-1342.

［5］贾建华，焦李成，柳炳祥.图像分割的谱聚类集成算法［J］.西安交通大学学报，2010，44（6）:93-98.

［6］刘爱平，付 琨，尤红建，等.基于MAR-MRF的SAR图像分 割 方 法［J］.电 子 与 信 息 学 报 ，2009，31（11）:2556-2562.

［7］高佳城，林岳松，陈华杰.基于像素分类的自适应SAR图像融合算法［J］.机电工程，2009，26（3）:16-19.

［8］李旭超.图像统计模型参数估计中的期望最大值算法［J］.中国图象图形学报，2012，17（6）:619-629.

［9］吴 锡，周激流，何建新.采用非局部主成分分析的极大似然估计图像去噪［J］.光子学报，2011，40（12）:1827-1831.

［10］唐 泉，樊晓平，黎 燕.基于分块聚类的车牌图像二值化方法［J］.计算机仿真，2010，27（3）:286-289.