小型化四足机器人的运动学分析及仿真研究*

2013-09-15 09:22徐晓希李吉祥郝焕瑞辛景雷

机电工程 2013年8期

王鹏，徐晓希，李吉祥，郝焕瑞，辛景雷

（哈尔滨理工大学机械动力工程学院，黑龙江哈尔滨 150080）

0 引言

在2011年3月日本发生的灾难破坏之大，造成的影响之深远，在历史上实属罕见，震级甚至达到了里氏9.0级。该地震的中心位置位于西太平洋内东经142.3°、北纬38.2°的地区，其震源深度非常大，超过18 km。经后续研究发现表明，由地震引发的海啸最大的峰值达到23 m之高。日本部分地区在地震及海啸的灾难中遭受了非常大的冲击，并有大量的人员伤亡［1］。地震发生在该月的11日，列举随后三天的伤亡报告:12日，在日本的东北部地区，死亡及失踪人数超过1 500名；13日，该项的统计人数超过3 000名，14日，人数急剧升到超过10 000名。而截至该月20日，死亡及失踪人数超过20 000名，数字触目惊心！同时灾难也造成了大量的建筑倒塌。

而灾难过后最主要的问题就是如何快速搜索在极其危险情况下的幸存人员［2-5］。经相关专家调查研究后发现，假如在搜索最佳时间72 h之内找不到幸存者，那么他们将因不能够得到及时的救助而极有可能死亡［6-9］。上述事实已经用血的教训来证明了这一点。

因此，用于灾后快速搜索特定目标的小型四足机器人开发将会是非常重要且十分必要的［10］。四足机器人既有优于两足机器人的平稳性，又可避免六足机器人机构的冗余和复杂性，此项研究工作具有一定的现实意义。

因此，本研究首先进行该小型化四足机器人的结构方案设计，这其中包括控制系统、减速传动机构、分解传动机构、间歇分配机构和腿部机构；然后，建立四足机器人简化模型的单腿D-H坐标系，并完成其运动学分析；最后应用ADAMS软件进行其步态切换的仿真及分析。

1 小型化四足机器人设计方案

该小型化机器人的运动方式是首先由动力机构提供动力，经减速机构将运转的速度减下来，从而提高了输出转矩，通过计算使转矩满足所有机构运动的要求，再由前、后身运动分配机构和调节机构将运动进行转化，成为周期、间歇性运动进行输出，最后分别传递到前身及后身行走机构上，执行行走功能，从而使得该小型化机器人实现稳定行走运动。

本研究将机器人的运动分为左、右侧两腿同时运动，而且精简所有不需要的机械结构，使机体尽可能减小质量，运动时机体非常轻便，在满足相应的运动时，对每个关节都使用高性能材料及高要求的加工工艺，保证其强度和刚度，进一步提高其运动时的平稳性。

其主要组成单元为:

（1）控制系统。由于机构相对复杂化，从而减轻了控制系统的工作量。该控制系统只控制位于机身中间位置的步进电机，给机器人的运动提供驱动力，该系统包括步进电机驱动装置，嵌入式集成电路控制系统。该系统作为控制中枢，通过向电机驱动装置发送脉冲指令，来控制电机的运转速度及转向，凭借步进电机把动力传递给蜗杆，实现动力的第一次传递。

（2）减速传动机构。由蜗轮、蜗杆、蜗杆支撑架、齿轮支撑架及相应辅助件（轴承、联轴器、螺栓、限位挡圈等）组成。通过联轴器接受步进电机传递过来的速度和扭转力，经过蜗轮蜗杆机构减速后，大幅度降低输出速度、增大输出力矩，使该速度达到机器人运动时的安全角速度的要求，有效增加了运动的平稳性和安全性。

（3）分解传动机构。由主动齿轮、前肢被动齿轮、后肢被动齿轮、齿轮支撑架及相应辅助件（轴承、限位挡圈等）组成。因主动齿轮和蜗轮系同轴传动，故其角速度在数值上近似相等，蜗轮将速度和扭转力经过心轴传递给主动齿轮，主动齿轮分别与前肢被动齿轮、后肢被动齿轮啮合传动，将运动进行分解到这两个齿轮上，由于该速度值已经适合机器人运动，该传动单元不需要再减速，属于等速传动，主要是将运动进行分解。由于齿轮传动机构具有传动平稳的特点，机构进一步增加了机器人运动的稳定性。

（4）间歇分配机构。以前肢为例，由前肢曲柄、前肢曲柄连接杆、前肢大腿及相应辅助件（螺栓、限位挡圈、限位销等）组成。前肢被动齿轮经主动齿轮传递给的动力，进行再次分配，分配对象为两侧的曲柄机构，此分配机构，原理以曲柄摆杆机构为依托，结合机器人结构方案需要的尺寸和运动进行设计，经过计算，确定符合要求的尺寸数值，使两侧的前肢腿部形成规律性、合理性且交替运动的机构。

（5）前身腿部机构。前肢足部、前肢小腿、前肢大腿、前肢小腿连接通销及相应辅助件（限位挡圈、限位销等）组成。间歇分配机构将运动传给曲柄，曲柄连接杆，大腿接受曲柄连接杆传递过来的运动，将运动再传递给小腿，小腿连接足部，进行摆腿运动。经过减速机构减速后，传到足部的速度已经可以实现平稳行走。腿部是最后一级执行机构，足部与地面相接触，承受地面产生的反作用力，对腿部结构经过设计，能够对该作用力进行缓冲，从而减小了该作用力对其他机构的冲击作用。

2 小型化四足机器人运动学分析

本研究对机器人简化模型进行正向运动学分析。机器人结构简图如图1所示。

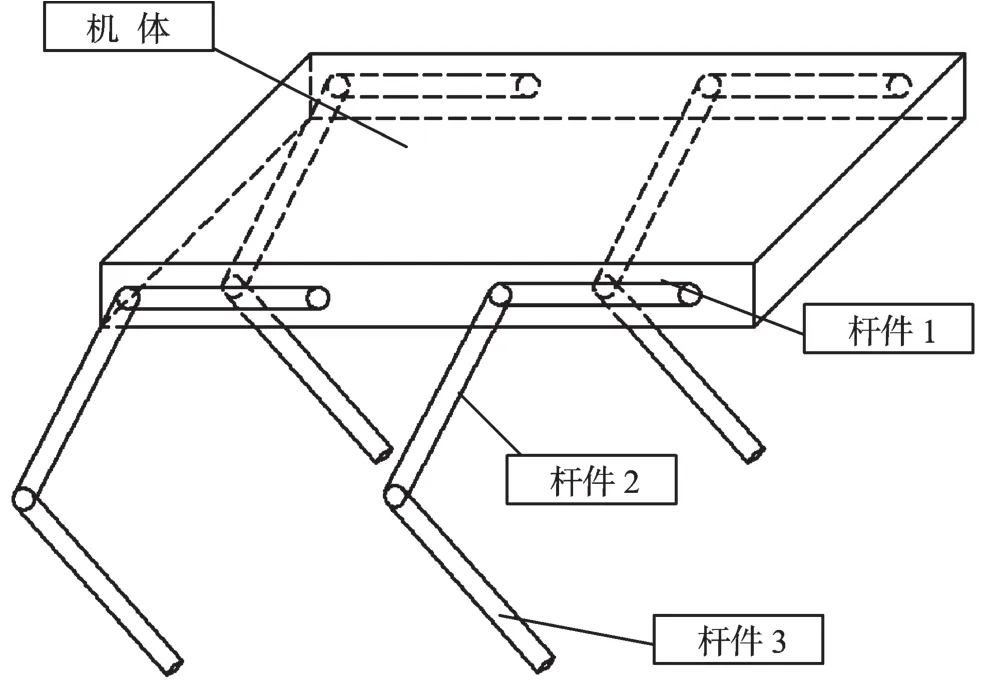
图1 小型化四足机器人结构简图

图1中，机体为箱状刚体，每条腿有3个转动关节，杆件1是360°旋转，杆件2是小范围移动，杆件3是最后执行机构，通过相互配合，达到向前行走的要求。

因机器人的每条腿结构相同，对其一腿进行研究即可，本研究将每一个杆件建立一个坐标系，并用齐次变换矩阵来描述相应的位置和姿态，建立机体的坐标系(Xb,Yb,Zb)，规定Xb正向为机器人前进的方向，Zb轴正向与重力方向相反，由右手定则推出Yb轴，(Xb,Yb,Zb)的原点在机坐标系中为(a,b,c)。四足机器人单腿杆件及关节参数如表1所示。

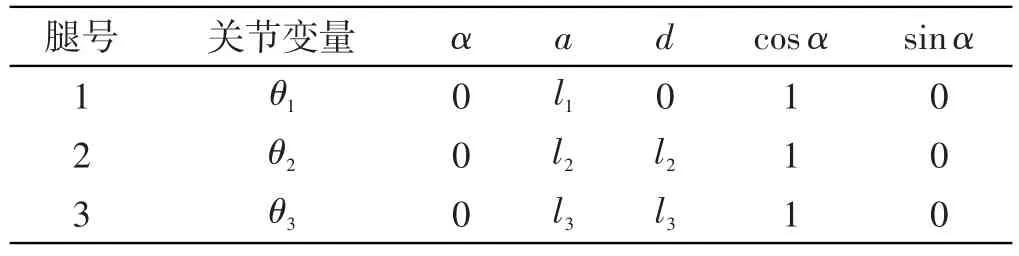
表1 四足搜救机器人单腿杆件及关节参数

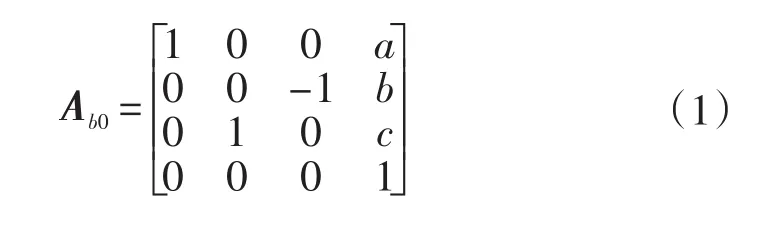
将表1参数代入式（1）中，可得如下矩阵:

式中:si=sinθi，ci=cosθi(i=1,2,3)。

足端在坐标系中的运动轨迹和始末点已知，设末端位姿矩阵为:

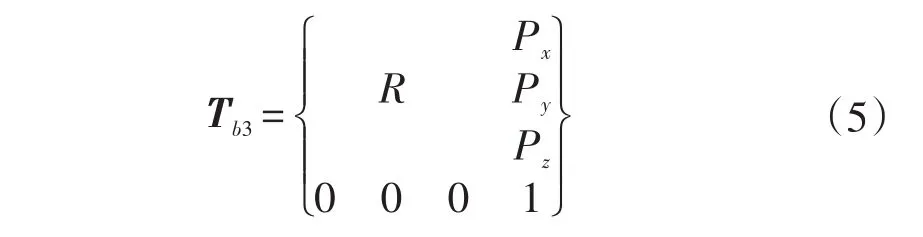
总变换矩阵经过整理得Tb3可表示为:

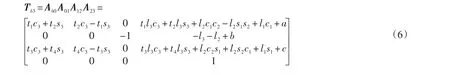
由式（5，6）可得:

式中:t1=t4=c1c2-s1s2；t2=-t3=-c1s2-s1c2；R—足部末端姿态矩阵；Px，Py，Pz—足部末端在X，Y，Z轴上的坐标。

为了核对结果的正确性，将此位置关节转角的初始值代入Tb3，则:

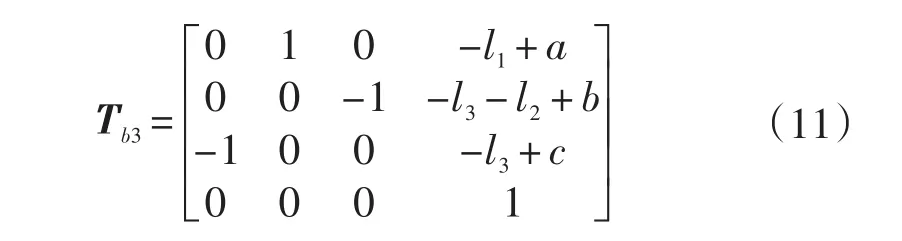
这一结果与图示位姿完全一致，证明上述推导运动学方程的正确性。

3 小型化四足机器人运动仿真

小型化四足机器人在实际运动的试验过程中，机体的各部件频繁运动，对相应参数进行分析是十分必要的，仿真分析在验证其方案正确性与可靠性方面都将起到至关重要的作用。因此借助成熟的仿真软件对该机器人进行运动仿真分析就显得非常重要。

ADAMS软件为其使用者提供了相应的建模和仿真环境，能够使用户对各种机械系统进行针对性的建模、仿真及分析。与其他相关机械仿真软件相比，该软件具有了强大的运动学和动力学分析功能。本研究运用ADAMS软件对小型化四足机器人进行了相应的运动分析。

本研究将运用Pro/E软件建立好的小型化四足机器人模型导入ADAMS软件中，利用Pro/E软件所做的装配模型如图2所示。

导入ADAMS后的小型化四足机器人模型如图3所示。

笔者将Pro/E文件转化成为ADAMS软件所支持的格式文件，并导入ADAMS软件后添加相应约束及所需动力进行处理。

图2 Pro/E软件中的小型化四足机器人模型

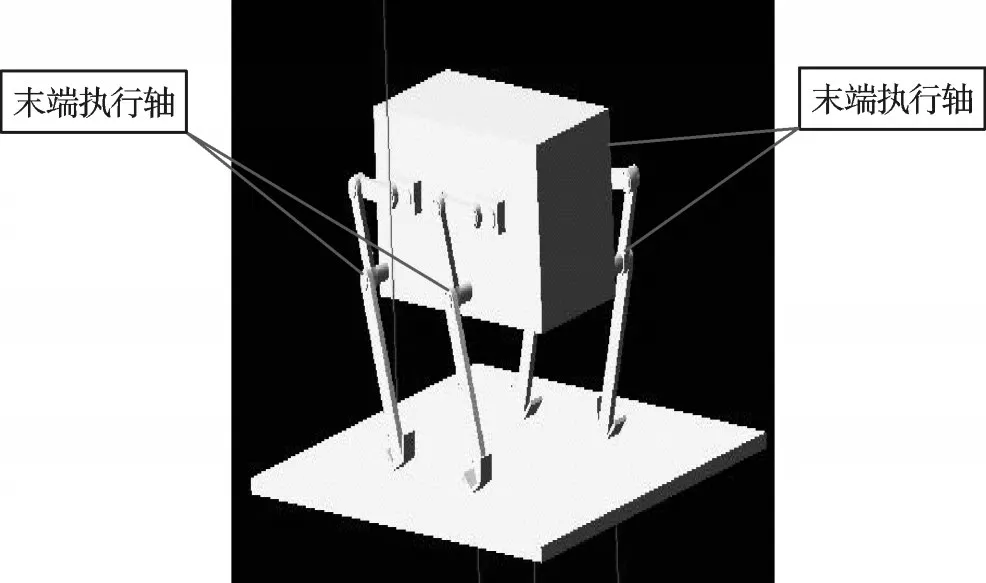
图3 导入ADAMS后的小型化四足机器人模型

该仿真的主要内容是通过对一侧腿部与对侧腿部进行步态切换时状态的分析，从而判断小型化四足机器人在行走时的稳定性与可靠性，一侧前腿速度曲线如图4所示。

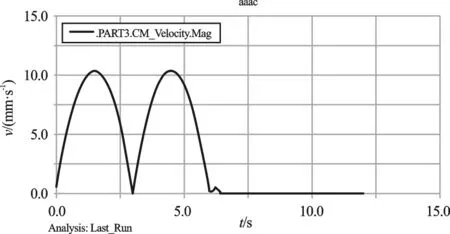
图4 一侧前腿速度曲线

对侧前腿速度曲线如图5所示。此处尖点的产生是由于一侧与二侧腿部在承载交换时所产生的，而图4、图5中两波谷没有接触底线，是由相应部件的传动误差所引起的。

通过图4、图5所描述的内容可知，除上述提及两个不可避免的问题外，分析结果表明该小型化四足机器人的运动是可靠且稳定的。

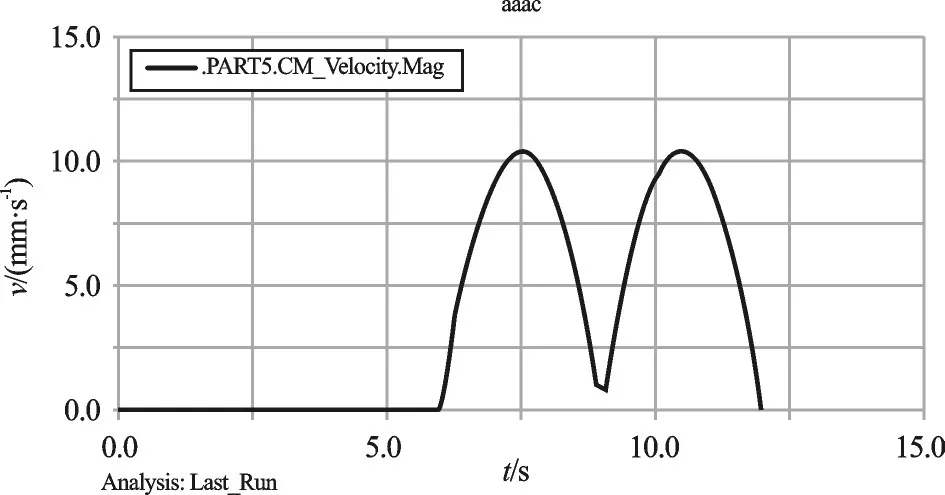
图5 对侧前腿速度曲线

4 结束语

在完成机构设计方案和运动学分析的基础上，本研究提出的一种小型化四足机器人的稳定步态切换设计得到了仿真实验验证，实验结果表明，该设计方案可以实现小型化四足机器人的协调行走功能，并为以后的优化四足机器人样机的研制提供了重要的技术参考和理论依据。

后续的研究工作中，本研究将考虑地形条件的变化，通过实际样机的行走实验来进一步优化结构设计，并深入研究小型化四足机器人稳定步态的控制方法。

（References）:

［1］王鹏，李鑫，江文浩.地震搜救机器人构型设计综述［J］.哈尔滨理工大学学报，2012，17（1）:15-19.

［2］张亚萍，马明星.搜救机器人系统的设计与开发［J］.中国制造业信息化，2010，39（5）:52-55.

［3］MARK J.Evolution and field performance of a rescue robot［J］.Journal of Field Robotics，2008，25（1）:17-30.

［4］钱善华，葛世荣.救灾机器人的研究现状与煤矿救灾的应用［J］.机器人，2006，28（3）:350-353.

［5］刘静，赵晓光，谭民.腿式机器人的研究综述［J］.机器人，2006，28（1）:81-88.

［6］何冬青，马培荪，曹冲振，等.四足机器人对角小跑起步姿态对稳定性的影响［J］.上海交通大学学报，2005，39（6）:880-882.

［7］计时鸣，刘毅，李研彪，等.一种新型拟人机械腿的运动传递性能分析［J］.机电工程，2012，29（10）:1125-1129.

［8］张文宇.四足机器人斜面全方位静态步行及稳定性分析［D］.青岛:中国海洋大学机电工程与自动化学院，2009:1-2.

［9］吉爱红，戴振东，周来水.仿生机器人的研究进展［J］.机器人，2005，27（3）:284-288.