关于特定幸福4次方数列＊

高 丽，赵喜燕，赵彩红

（延安大学数学与计算机科学学院，陕西延安 716000）

关于特定幸福4次方数列＊

高 丽，赵喜燕，赵彩红

（延安大学数学与计算机科学学院，陕西延安 716000）

利用初等方法对特定幸福4次方数列及特定幸福n次方数列进行了研究，给出并证明了关于集合F4的定理，并且得出特定幸福n次方数列相关问题的求解方法.

初等方法；特定幸福立方数；特定幸福4次方数

1993年，美籍罗马尼亚著名数论专家Smarandache教授［1］提出了105个Smarandache未解决的问题，其中包含Smarandache数、Smarandache函数等内容.特定幸福立方数是Jebreel M教授［2］在研究Smarandache问题时引入的.这些内容引起了不少数论专家学者的兴趣，取得了一系列重要的研究成果［3－5］.

韩迪［6］解决了特定幸福立方数的相关问题，即F3＝｛1，153，370，371，407｝.类似于特定幸福立方数，笔者提出特定幸福4次方数，即：对任意正整数n，如果n的各位数字的4次方相加所得之值恰好等于n，那么这个正整数n就称为特定幸福4次方数.

例如，1＝14，1 634＝14＋64＋34＋44，8 208＝84＋24＋04＋84，...，则称1，1 634，8 208等是特定幸福4次方数.设F4＝｛1，1 634，8 208，9 474，...｝表示所有特定幸福4次方数的集合.笔者在文献［7－8］的基础上，利用初等方法得出如下结论：

定理1 设F4表示所有特定幸福4次方数的集合，则集合F4是有限集，且F4＝｛1，1 634，8 208，9 474｝，即这个数列中有4个元素，并且不包含素数.

在证明定理1之前，先给出以下数据：04＝0，14＝1，24＝16，34＝81，44＝256，54＝625，64＝1 296，74＝2 401，84＝4 096，94＝6 561.

证明 设As是特定幸福4次方数列｛an｝中的一个元素，假定As的十进制表示式为a1a2...as－1as，其中1≤a1≤9，a2，...，as－1，，as∈［0，9］.于是由特定幸福4次方数的定义，有

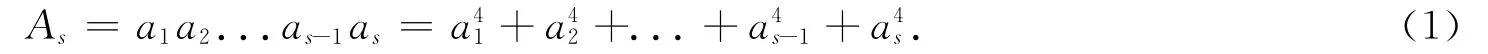
显然，由（1）式表示不难得出

即s必须满足不等式10s－1≤94×s.设函数f（s）＝10s－1－6 561s，则f′（s）＝10s－1·ln 10－6 561.当s≥6时，显然有f′（s）＝105·ln 10－6 561＞0，所以当s≥6时，f（s）为递增函数且f（6）＝60 634＞0，因此由单调递增函数的性质可知对所有s≥6，有f（s）＞0，从而对所有整数s≥6，有不等式10s－1＞94×s.这与不等式（2）矛盾.所以，要使不等式（2）成立，必须有s≤5.以下分s＝1，2，3，4，5这5种情况讨论.

当s＝5时，令A5＝a1a2a3a4a5，并且有1≤a1≤9，a1，a2，a3，a4，a5∈［0，9］.由A5的取值范围为10 000≤A5≤32 805，可以得出a1＝1，a1＝2或者a1＝3，这时用计算机编程来验证是否存在这样的A5.计算机程序为Java程序，最终答案是否定的.

也可以直接证明5位数中没有特定幸福4次方数.事实上当a1＝3时，max A5≤94×4＋34＝26 325，而此时30 000≤A5≤32 805，不在A5的取值范围内，故不成立.当a1＝2时，max A5≤94×4＋24＝26 260，则20 000≤A5≤26 260，从不等式不难推出a2＝0，1，2，3，4，5，6.

（1）当a2＝6时，A5≤94×3＋64＋24＝20 995，而26 000≤A5≤26 260，不成立.

（2）当a2＝5时，A5≤94×3＋54＋24＝20 324，而25 000≤A5≤25 999，不成立.

（3）当a2＝4时，A5≤94×3＋44＋24＝19 955，而24 000≤A5≤24 999，不成立.

（4）当a2＝3时，A5≤94×3＋34＋24＝19 780，而23 000≤A5≤23 999，不成立.

（5）当a2＝2时，A5≤94×3＋24＋24＝19 780，而22 000≤A5≤22 999，不成立.

（6）当a2＝1时，A5≤94×3＋14＋24＝19 700，而21 000≤A5≤21 999，不成立.

（7）当a2＝0时，A5≤94×3＋04＋24＝19 699，而20 000≤A5≤20 999，不成立.

当a1＝1时，max A5≤94×4＋14＝26 245，则10 000≤A5≤19 999，由此得出0≤a2≤9.

当a2＝0时，即a1＝1，a2＝0，max a4，a5≤9.现在考虑a3的取值范围，得到14＋04＋＋94×2≥10 000.解此不等式可得a3≥0.

当a3＝0时，即a1＝1，a2＝a3＝0，max a5≤9，14＋04＋04＋＋94≥10 000，解得a4≥8.

（ⅰ）当a4＝8时，A5≤14＋04＋04＋84＋94＝10 658，再考虑a5的取值范围，14＋04＋04＋84＋≥10 080，解得a5≥9.此时A5＝14＋04＋04＋84＋94＝10 658≠10 089，不成立.

（ⅱ）当a4＝9时，A5≤14＋04＋04＋94＋94＝13 123，再考虑a5的取值范围，14＋04＋04＋94＋≥10 090，解得a5≥8.

（a）当a5＝8时，A5＝14＋04＋04＋94＋84＝10 658≠10 098，不成立.

（b）当a5＝9时，A5＝14＋04＋04＋94＋94＝13 123≠10 099，不成立.

用同样的方法，可以讨论a3＝1，...，9的情况，进而讨论a2＝1，...，9的情况.通过讨论发现，5位数中没有特定幸福4次方数.类似地，讨论s＝4，3，2，1的情况，得出F4＝｛1，1 634，8 208，9 474｝.从而证明了幸福4次方数是有限的，且只包含4个数，并且没有素数.

［1］ SMARANDACHE F.Only Problems，Not Solutions［M］.Chicago：Xiquan Publishing House，1993.

［2］ MUNEER JEBREEL.Smarandache Sequence of Happy Cube Numbers［J］.Smarandache Notions Journal，2004，1 4（1）：139－140.

［3］ 张 沛.一个包含伪Smarandache无平方因子函数的方程［J］.郑州大学学报：理学版，2008，40（2）：36－38.

［4］ 蔡立翔.一个包含数论函数的方程及其正整数解［J］.郑州大学学报：理学版，2008，40（2）：33－35.

［5］ WANG Jin-rui.On the Smarandache Function and the Fermat Numbers［J］.Scientia Magna，2008，4（2）：25－28.

［6］ 韩 迪.关于特定幸福立方数列［J］.郑州大学学报：理学版，2012，44（3）：20－22.

［7］ 张文鹏.初等数论［M］.西安：陕西师范大学出版社，2007.

［8］ APOSTOL T M.Introduction to Analytic Number Theory［M］.New York：Springer-Verlag，1976.

（责任编辑 向阳洁）

Sequence of Fixed Happy 4-th Numbers

GAO Li，ZHAO Xi-yan，ZHAO Cai-hong

（School of Mathematics and Computer Science，Yan’an University，Yan’an 716000，Shaanxi China）

By using the elementary methods，fixed happy 4-th numbers and fixed happy n-th numbers are studied.A theorem about the set of F4is given and proven，and series of solutions of the problems related to fixed happy n-th numbers are obtained.

elementary method；fixed happy cube number；fixed happy 4-th number

O156.4

A

10.3969／j.issn.1007－2985.2013.05.001

1007－2985（2013）05－0001－02

2013－03－07

国家自然科学基金资助项目（10271093）；陕西省教育厅专项科研计划资助项目（07JK430）；延安大学自然科学专项科研基金资助项目（YDZ2013－04）

高 丽（1966－），女，陕西绥德人，延安大学数学与计算机科学学院教授，硕士生导师，主要从事数论研究.