带固定交易费用的模糊投资组合*
成央金,余 双,罗晓琴,于瑞华
(湘潭大学数学与计算科学学院,湖南湘潭 411105)
带固定交易费用的模糊投资组合*
成央金,余 双,罗晓琴,于瑞华
(湘潭大学数学与计算科学学院,湖南湘潭 411105)
基于区间规划的方法,研究了带固定交易费用下的模糊投资组合模型.在模型中引进正态隶属函数;考虑投资组合风险偏好时,修改了一般投资组合中风险偏好方法定义方法,使其更符合区间规划;在考虑未来回报率时,考虑了符合实际情况的因素——涨跌停板;引进新的流动性的定义方法,改正了以往用换手率带来的缺陷.
组合投资;区间规划;正态隶属函数;涨跌停板
1 问题的提出
1952年Markowitz H[1]提出了投资组合理论,将数据工具引入到金融问题中研究.1958年Modiliani F等[2]发表了MM理论,这2个理论奠定了现代金融学理论的基础.近60年来,无数的学者在这2个理论的基础上不断地创新和发展,提出新的理论.
由于用经典的均值-方差(M-V)模型来度量一个投资组合模型时,其资产的收益呈正态分布或投资者的效用函数是二次的,但是在实际中这些条件往往难以满足,并且如果投资风险资产的个数过多时,计算风险资产收益协方差也比较难;因此,人们依据对风险的不同定义,提出不同的风险函数.如1970年,Mao提出下半方差风险函数模型;1991年,Konno H等[3-4]提出基于绝对偏差函数的投资组合模型;2000年,Teo K L等[5]在下行风险度的基础上翻,推出HT∞函数,考虑在估计风险时将历史数据划分了T个阶段来估计;2000年,Gaivoronski在以下行风险度为前提,构造出以VAR为风险度量的投资组合模型;2001年,Cai X Q等[6]在绝对偏差的基础上提出l∞风险函数;2001年,Roekafellar在VAR的基础上提出以CVAR为风险度量指标构建投资组合模型.
在真实的交易市场中,受到市场、经济、国家的宏微观调控及不可抗拒的自然因素的影响,投资者对投资的未来回报率是不确定的,投资者很难得到一个真实的值,而区间数是一个很好的解决此问题的方法.在1980年,Bitran提出带模糊区间系数的规划问题,首次将区间数引入数学规划问题中.在1998年,Ramaswany将一般模糊数的规划应用到投资组合问题中,不过该模型仅考虑了收益,没有考虑风险目标.在2002年,K.K.Li等[7]讨论了基于2个间隔之间的模糊不等式,建立了新的含参数的线性规划问题.在2008年,Zhang Wei-guo等[8]建立了基于区间估计可能性均值和可能性方差的模型.在2011年,Liu Shang-tai[9]讨论了在资产收益是区间数时的不确定投资选择问题,通过绝对偏差构建了一个2级的数学规划模型.
在以往的研究中,人们考虑收益的模糊区间时,凭借的是个人的直觉或者是通过梯形或三角形隶属函数,凭个人直觉不太科学,而用梯形或三角形来模拟,虽然能够比较好地得到区间数,但是不太符合数连续变化的情况,而且容易与实际情况不符——投资市场上对每个资产的涨跌都有限制,只能在这个限制范围内交易.
一个好的证券必须有良好的流动性,只有这样,投资者才能够从容地进行买卖,才能不被股市套死,所以在进行投资时,必须考虑到这一点.在以往的研究中,研究者往往就是将股票的换手率看成股票的流动性,这种做法有点缺陷.笔者引进新的方法来度量流动性,使其更加符合市场规律.
在投资市场中,每笔投资都有成本,有时虽然投资赚了,但是可能赚的钱还不够支付投资成本,故在考虑投资组合的时候,必须考虑交易费用.
笔者基于不确定规划问题,引入正态隶属函数和涨跌板联合来估计投资的未来收益额,引入新的偏好因子定义方法,并考虑带固定交易费用和证券的流动性的情形,建立了新的投资组合模型.
2 预备知识
2.1 可能性均值和λ-截集
先给定一些定义,论域X到[0,1]闭区间上的任意映射μA:X→[0,1],x→μA(x),都确定X上的一个模糊集合,μA称为的隶属函数,(x)称为x对模糊集的隶属度,记为={(x,μA(x))|x∈X}.使(x)=0.5的点x0称为模糊集的过渡点,此点最具模糊性.显然,模糊集合完全由隶属函数来刻画,当(x)={0,1}时退化为一个普通集.

由市场未来的不确定性,投资者不能根据历史数据和市场消息得到确定的、未来的回报额.假设其满足基于正态分布的隶属函数,即则的λ-截集可表示为[]λ=[α-σ

2.2 可能性预期回报额
在真实的交易市场,有涨跌停板制度的限制.涨跌停板制度是指,期货合约在一个交易日中的成交价格不能高于或低于以该合约上一交易日结算价为基准的某一涨跌幅度,超过该范围的报价将视为无效,不能成交.在涨跌停板制度下,前交易日结算价加上允许的最大涨幅构成当日价格上涨的上限,称为涨停板;前一交易日结算价减去允许的最大跌幅构成价格下跌的下限,称为跌停板.以中国证券市场为例,一般A股的涨跌幅以10%为限,当日涨幅达到10%限为上限,称为涨停板;当日跌幅达到10%限为上限,称为跌停板.
将最大限度回报额与可能性均值联合起来考虑,则资产i的未来回报额为ri=,),其中

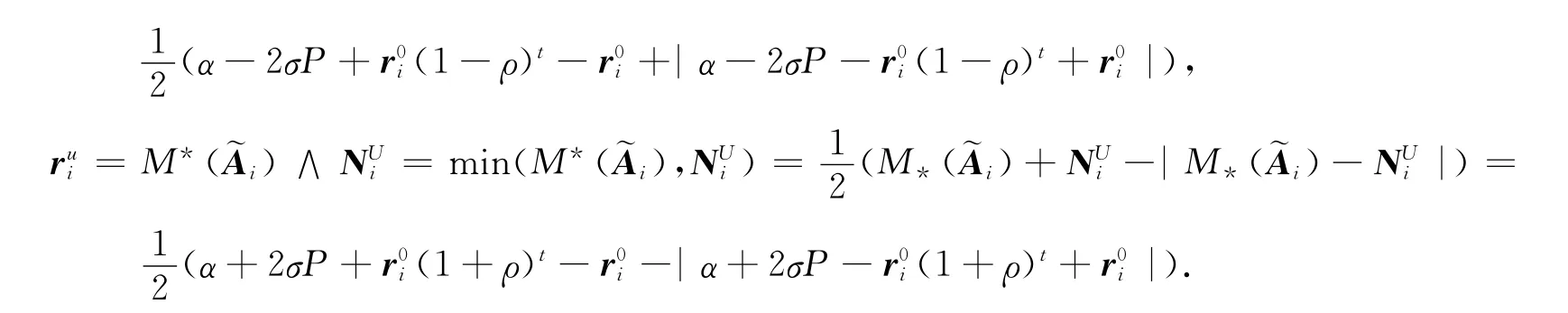
2.3 证券组合的流动性原则
流动性原则即变现性原则,是指证券组合所形成的资产在不发生价值损失的前提下,可随时转变为现金,以满足投资者对现金支付的需要.投资所形成的不同资产有不同的流动性.
但是在金融市场上,证券的流动性是一个非具体的、不能够直接通过观察得到的数据.一个理想的衡量证券的流动性指标应包含这3个方面:价格波动,即证券的价格不变或微小改变;时间,即证券在卖出或买入后的价格的变化快慢;成交量,即证券交易数量.
在以往的组合投资模型中,研究者都是用换手率来衡量证券的流动性,但是换手率没有反映成交量对价格波动的影响,因此没有反映流动性的本质特征.笔者没有用换手率来衡量证券流动性,而是选用收益额的绝对值与换手率之比来衡量流动性,它能比较客观真实地反映证券的流动性情况.该指标越大,市场流动性越低,该指标越小,市场流动性越高.因收益额是一个区间值,故流动性也是一个区间值[11].
2.4 偏好因子
对于不确定的投资组合问题,决策者会因为自身的性格、所在的地域等多重因素的影响,对不同的投资有不同的风险偏好关系.风险偏好,可以使用标准赌博技术(SGT)来确定,其中比较普遍的是赌博当量法.这是让决策人面对一种测试赌博,一好一坏2种结果,发生的概率已知,然后令其评价介于两者之间的某一结果值,要求它与赌博的价值完全相等,称此结果值为赌博的当量,并将其值记为τ.
基于赌博当量法的思路,给出不确定区间数的基于风险偏好的表示方法.假定a在区间=[xl,xu]均匀分布,密度函数为f(a)=1/(xu-xl),则ϑe(),其中ϑ为风险偏好因子(|ϑ|≤0.5),表示承担的风险偏好,n()为区间数的中点值,e()为区间数的宽度.当ϑ<0时,表示投资者是风险厌恶,ϑ越接近-0.5,投资者厌恶的程度越高;当ϑ=0时,表示投资者是风险中立的;当ϑ>0时,表示投资者是风险喜爱的,ϑ越接近0.5,投资者喜爱的程度越高.
3 考虑带固定交易费用的模糊投资组合模型
在投资市场,投资者要付出各种交易费用是指,投资者在委托买卖证券时应支付的各种税收和费用的总和,以中国为例,通常包括印花税、佣金、过户费、其他费用等几个方面的内容.(1)印花税.印花税是根据国家税法规定,在股票(包括A股和B股)成交后对买卖双方投资者按照规定的税率分别征收的税金.(2)佣金.佣金是指投资者在委托买卖证券成交之后按成交金额的一定比例支付给券商的费用.(3)过户费.过户费是指投资者委托买卖的股票、基金成交后买卖双方为变更股权登记所支付的费用.(4)其他费用.其他费用是指投资者在委托买卖证券时,向证券营业部缴纳的委托费(通讯费)、撤单费、查询费、开户费、磁卡费以及电话委托、自助委托的刷卡费、超时费等.
由此可见,证券的交易费用除了一部分与证券的交易量有关外,还有一部分与证券的交易量无关,假设无关部分的费用总量为xn+1.
假设证券投资者初期所拥有的风险资产为x0=(,x,...,x),经过一段投资期后,所拥有的风险资产变为x=(x1,x2,...,xn).假设u=(u1,u2,...,un)为投资的上限,并其限制卖空.假设证券投资交易费用中与交易额有关部分的交易费用与交易额成正比,设比例系数为k,则总的交易费用为k(x)=
假设投资者投资的总量为M,ri=,]表示资产i的预期回报额,Ri表示资产i的随机回报率,则绝对偏差风险函数为
用li=[,]表示资产i的流动性值,turni表示资产i的换手率.l0表示投资者给出的流动性的值的要求.由资产的流动性可得到xili≤l0,li=|ri|/turni.那么,带固定交易费用的平均绝对模糊投资组合模型为

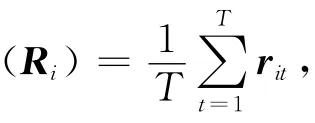

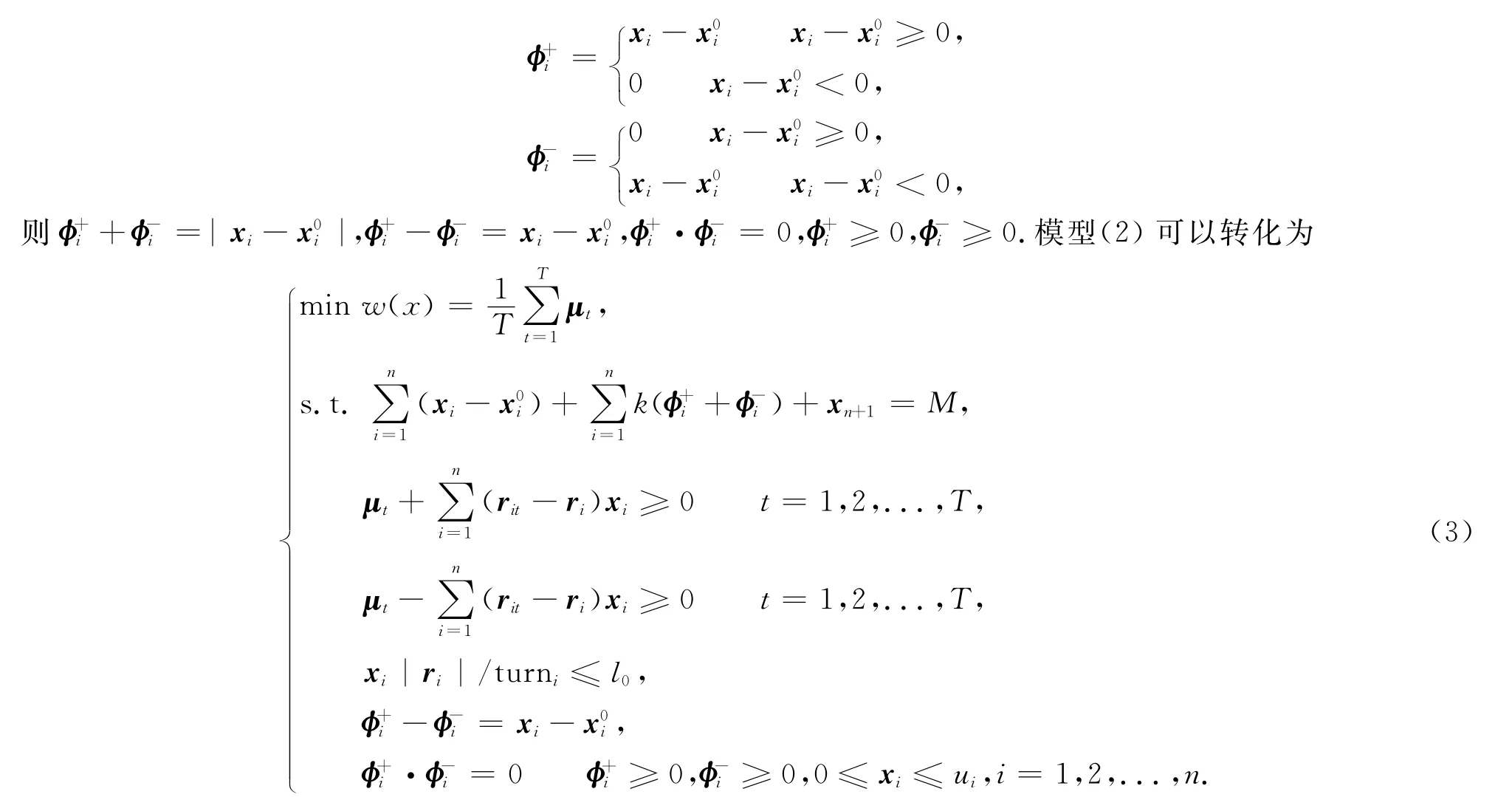

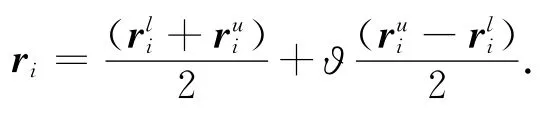

对投资者而言,投资者目的是要求赚钱,故对所投资的股票而言,如果对它的未来收益估计是负面的状态,也就是说对股票而言,投资者预期在持有某支股票的期间内,股票的价格是下跌的,则投资者不会持有这支股票,会将它抛售.所以,对模糊的投资组合而言,股票未来收益额ri的区间[,]中的,,根据投资者的要求可得||<.

由于模型(6)是一个线性的模型,因此可以用求解线性规划的软件包Lindo或是用Matlab对其求解,得到投资者满意的投资策略.
4 结语
根据模糊规划,基于绝对偏差风险函数,建立了全新的带固定交易费用的模型.在模型中,引入正态隶属函数和涨跌停板联合来估计未来的回报额,这种方法能够更加客观反应对未来回报额的估计.引入新的流动性定义方法,使其能够更加直接体现资产在投资中的流动方便性.对于风险偏好因子,不再简单地用λ(λ∈[0,1])来估计,而是用赌博当量法来评估投资者的风险偏好,这样符合人们的客观感觉.
对金融市场的摩擦因素,只考虑了带固定交易费用的情况,但是在实际的教育市场中,还存在许多大量的因素,如可变交易费用、买卖价差等,这些不同的因素会影响投资者的投资者策略.在估计投资者的回报额时,应尽管考虑得比较全面,但也有些缺陷,如人们的心理因素变化——羊群效应,单个投资者总是根据其他同类投资者的行动而行动,在他人买入时买入,在他人卖出时卖出.此外,实际的投资过程是一个动态的投资过程,笔者考虑的只是单阶段(静态)投资过程,如何将其推广到动态的情形,另外在股市中,投资的股票数量只能是十或百的整数倍,笔者没有考虑此种情形,这些问题都值得研究.
[1] MARKOWITZ H.Portfolio Selection[J].The Journal of Finance,1952,7(1):77-99.
[2] MODIGLIANI F,MILLER H M.The Cost of Capital,Corporationb Finance and the Theory of Investment[J].American Economic Review,1958,48:261-297.
[3] KONNO H,YAMAZAKI H.Mean-Absolute Deviation Porfolio Optimization Model Its Applications to Tokyo Stock Market[J].Managenment Science,1991,37:519-529.
[4] KONNO H.Portfolio Optimization Using L1Risk Function IHSS Report 88-9,Institue of Human and Social Sciences[M].Tokyo:Tokyo Institute of Technologe,1988.
[5] TEO K L,YANG X Q.Portfolio Selection Problem with Minimax Type Risk Function[J].Annals of Operations Research,2001,101:333-349.
[6] CAI X Q,TEO K L,YANG X Q,et al.Portfolio Optimization Under a Minimax Rule[J].Managenment Science,2000,46:957-972.
[7] LI K K,WANG S Y,XU J P,et al.A Class of Linear Interval Programming Problems and Its Application to Portfllio Selection[J].IEEE Transactions on Fuzzy Systems,2002,10:698-703.
[8] ZHANG Wei-guo,ZHANG Xi-li,XIAO Wei-lin.Portfolio Selectionunder Possibilistic Mean-Variance Utility and a SMO Alforithm[J].European Journal Operational Research,2009,197:693-700.
[9] LIU Shang-tai.The Mean-Absolute Deviation Portfolio Selection Problem with Interval-Valued Returns[J].Tournal of Computational and Applied Mathematics,2011,235:4 149-4 157.
[10] CARLSSON C,FULLÉR R,MAJILENDER P.On Possibilistic Mean Value and Variance of Fuzzy Numbers[J].Fuzzy Sets and Systems,2000,115:315-326.
[11] 张志鹏,杨朝军.流动性与收益、收益波动的动态关系[J].系统工程理论方法应用,2006,10(5):393-398.
(责任编辑 向阳洁)
Fuzzy Portfolio with Fixed Transaction Costs
CHENG Yang-jin,YU Shuang,LUO Xiao-qin,YU Rui-hua
(School of Mathematics of Computational Science,Xiangtan University,Xiangtan 411105,Hunan China)
This paper,based on the interval planning method,studies the fuzzy portfolio selection model with fixed transaction costs.The model introduces the function of normal membership,and at the same time,considers the portfolio risk preference.The general portfolio risk preference method definition method is thus modified,which is more consistent with the interval programming,and taking into account the future rate of return,considers the actual situation factors-limit up and limit down.New liquidity definition method is introduced,and the previous defect brought out by turnover rate is overcome.
portfolio;interval planning;function of normal membership;limit up and limit down
O224
A
10.3969/j.issn.1007-2985.2013.05.006
1007-2985(2013)05-0021-06
2013-01-07
国家自然科学基金资助项目(51075345)
成央金(1965-),男,湖南娄底人,湘潭大学数学与计算科学学院教授,主要从事最优化理论与算法设计研究.
——基于三元VAR-GARCH-BEEK模型的分析

