非平衡2n－周期二元序列的5－错误序列＊

周建钦，王洪翠

（1.杭州电子科技大学通信工程学院，浙江杭州 310018；2.安徽工业大学计算机学院，安徽马鞍山 243032）

非平衡2n－周期二元序列的5－错误序列＊

周建钦1，2，王洪翠1

（1.杭州电子科技大学通信工程学院，浙江杭州 310018；2.安徽工业大学计算机学院，安徽马鞍山 243032）

线性复杂度和k－错线性复杂度是密钥流序列随机性检测及其稳定性度量的2项重要指标，对衡量密钥流序列密码强度具有极其重要的意义.计算序列k－错线性复杂度的一个行之有效的方法是，分析研究汉明重量最小的错误序列.在此基础之上，给出了5－错线性复杂度不大于2n－3、等于2n－2－2m和2n－2－2m＋x时错误序列的计数公式，并通过计算机编程进行了验证.

密钥流序列；k－错线性复杂度；k－错误序列

流密码是保密通信中一个重要的密码体制，线性复杂度和k－错线性复杂度分别用来度量密钥流序列的随机性和稳定性.为了防止攻击者通过B-M算法［1］分析出整个序列，要求密钥流序列的线性复杂度足够大.然而现实通信过程中是存在干扰的，当改变序列少量比特时，有的序列的线性复杂度会急剧下降，例如24－周期二元序列s（4）＝｛1100 0000 1000 0000 ｝0000｝，线性复杂度为16，这是其线性复杂度能够达到的最大值.改变s（4）中1个非0比特，得到＝｛1000 0000 1000 0000｝后，其线性复杂度变为8，当改变3个非0比特得到全0序列时，其线性复杂度则下降至0.显然这样的序列是不稳定的，这就是密码学意义上的弱序列.

丁－肖－单［2］最早注意到密钥流序列的不稳定性问题，随后Stamp M等［3］引入k－错线性复杂度的概念，将其作为度量序列稳定性的一个指标.之后，Kurosawa K等［4］进一步提出错误序列的概念.2008年，戚文峰等［5］给出k－错误序列的定义，并且认为对数值较小的k，要有较少的k－错误序列，以减少线性复杂度下降的概率.

通过文献［6］提出的计算k－错线性复杂度行之有效的方法，即将其转化为求汉明重量最小的错误序列，笔者给出在k＝5时，非平衡2n－周期二元序列当5－错线性复杂度不超过2n－3或等于2n－2－2m和2n－2－2m＋x时错误序列的计数公式M5（s（n））.

1 预备知识

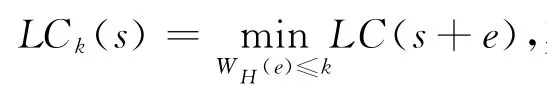
定义2［8］设周期为N的序列s和e，序列s的k－错线性复杂度为LCk（s）.若e满足LC（s＋e）＝LCk（s），1≤WH（e）≤k，则称e为s的k－错误序列.

记序列s的k－错误序列总数为Mk（s）.

引理2［8］设2n－周期二元序列s（n），若LC（s（n））＝2n，则s（n）的一个周期内的汉明重量为奇数；若LC（s（n））＜2n，则s（n）的一个周期内的汉明重量为偶数.

引理3［8］设Ei是周期为2n的二元序列，且序列一个周期内只有第i位上的元素是1，其他元素全为0，0≤i＜2n.若j－i＝2r（1＋2a），a≥0，0≤i＜j＜2n，r≥0，则LC（Ei＋Ej）＝2n－2r.

2 非平衡2n－周期序列的5－错误序列

定理1 设s（n）是2n－周期二元序列，且LC5（s（n））＝c，当1≤c≤2n－3时，有M5（s（n））＝1.

证明 设s（n）＝p（n）＋u（n），s（n）＝q（n）＋v（n），且LC（p（n））＝LC（q（n））＝c，WH（u（n））＝1，3或5，WH（v（n））＝1，3或5.

假设u（n）≠v（n），因为p（n）＋u（n）＝q（n）＋v（n），所以p（n）＋q（n）＝u（n）＋v（n）.根据引理1，LC（p（n）＋q（n））＜c≤2n－3，而u（n）＋v（n）最多呈8等分分布，由Games-Chan算法可知LC（u（n）＋v（n））≥2n－3.从而假设不成立，u（n）＝v（n），s（n）的5－错误序列只能为u（n），即M5（s（n））＝1.

证毕.

例1 当n＝4，c＝2时，序列s（4）＝｛1110 1110 1000 0000｝，LC5（s（4））＝2，只有1个错误序列e（4）＝｛0100 0100 0010 1010｝；当n＝4，c＝1时，序列s（4）＝｛1111 1110 1100 1100｝，LC5（s（4））＝1，也只有1个错误序列e（4）＝｛0000 0001 0011 0011｝.

定理2 设s（n）是2n－周期二元序列，LC（s（n））＝2n，LC5（s（n））＝2n－2－2m，n≥4，0≤m≤n－4，则M5（s（n））＝1，2或3.

证明 设序列s（n）＝p（n）＋u（n），LC（p（n））＝2n－2－2m，WH（u（n））＝1，3或5，另设序列v（n），WH（v（n））＝1，3或5，使得LC5（s（n））＝LC5（p（n）＋u（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m.

（1）当LC（u（n）＋v（n））＜2n－2－2m时，根据引理1，有LC5（s（n））＝LC5（p（n）＋u（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m.此时，u（n）＋v（n）呈4等分分布，根据引理2，有WH（u（n）＋v（n））＝8.

（Ⅰ）WH（u（n））＝3时，根据引理3，将u（n）分成2m＋1个子序列，每个子序列中任意2bit间的距离均为2m＋1的整数倍，即子序列中的各个比特之间的位置关系满足｛i，i＋2m＋1，...，i＋（2n－m－1－2）·2m＋1，i＋（2n－m－1－1）·2m＋1｜0≤i≤2m＋1－1｝.

此时，u（n）中的3个非0比特只能在同一子序列，且仅有2个非0比特相距2n－2的整数倍.在这种情况下，满足WH（v（n））＝5，LC5（s（n））＝LC5（p（n）＋u（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m的序列v（n）只有1个，亦或v（n）＝u（n），故有M5（s（n））＝2.

（Ⅱ）当WH（u（n））＝5时，同样将u（n）分成2m＋1个子序列，子序列中每个比特之间的距离为2m＋1的整数倍.

（ⅰ）若u（n）中的5个非0比特属于同一子序列.

（a）当u（n）中有3个非0比特（z1，z2，z3），它们之间的距离均为2n－2的整数倍，另外2个非0比特（z4，z5）之间的距离也为2n－2的整数倍时，仅存在1个序列v（n），WH（v（n））＝3，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m，亦或v（n）＝u（n），故有M5（s（n））＝2.

（b）当非0比特（z1，z2，z3）之间的距离仍为2n－2的整数倍，而（z4，z5）之间的距离不为2n－2的整数倍时，则有2个序列v（n），WH（v（n））＝5，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m，亦或v（n）＝u（n），故有M5（s（n））＝3.

（c）当分别有2对非0比特的距离为2n－2的整数倍时，仅有1个v（n），WH（v（n））＝5，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m，亦或v（n）＝u（n），故有M5（s（n））＝2.

（ⅱ）若u（n）中有4个非0比特在同一个子序列.

（a）此时，若4个非0比特中的3个比特间两两相距2n－2的整数倍，则只有1个序列v（n），WH（v（n））＝5，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m，亦或v（n）＝u（n），故有M5（s（n））＝2.

（b）若分别有2对非0比特间的距离为2n－2的整数倍，也只有1个序列v（n），WH（v（n））＝5，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m，亦或v（n）＝u（n），故有M5（s（n））＝2.

（2）当LC（u（n）＋v（n））＞2n－2－2m时，根据引理1，有LC5（s（n））＞2n－2－2m.然而LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m，此时有M5（s（n））＝1.

综上所述，M5（s（n））＝1，2或3.

证毕.

例2 当n＝4，m＝0时，序列s（4）＝｛1100 1100 1001 1000｝，LC5（s（4））＝3，其5－错误序列有2个，分别为＝｛0000 0000 0101 0100｝＝｛0101 0101 0000 0001｝.

定理3 设2n－周期二元序列s（n），LC（s（n））＝2n，LC5（s（n））＝2n－2－2m＋x，n≥5，2≤m＜n－3，0＜x＜2m－1，则M5（s（n））＝1，2，3或2n－m－2.

证明 设序列s（n）＝p（n）＋u（n），LC（p（n））＝2n－2－2m＋x，WH（u（n））＝1，3或5，另设序列v（n），WH（v（n））＝1，3或5，使得LC5（s（n））＝LC5（p（n）＋u（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m＋x.此时，u（n）＋v（n）呈4等分分布，根据引理2，有WH（u（n）＋v（n））＝8.

（1）LC（u（n）＋v（n））＜2n－2－2m＋x时，LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m＋x.

（Ⅰ）WH（u（n））＝3时，根据引理3，将u（n）分成2m个子序列，每个子序列中的任意2bit间的距离均为2m的整数倍.为了满足情况（1），u（n）中的3个非0比特只能在同一个子序列中.

当3个非0比特中只有2个比特的距离为2n－2的整数倍时，只存在1个序列v（n），WH（v（n））＝5，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m＋x，亦或v（n）＝u（n），故有M5（s（n））＝2.

（Ⅱ）当WH（u（n））＝5时，同样先将u（n）分成2m个子序列，子序列中的每个比特之间的距离为2m的整数倍.

（ⅰ）若u（n）中的5个非0比特在同一子序列中.

（b）若其中有3个非0比特（z1，z2，z3）的距离为2n－2的整数倍，而另外2个非0比特（z4，z5）之间的距离也为2n－2的整数倍时，则有1个序列v（n），WH（v（n））＝3，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m＋x，亦或v（n）＝u（n），故有M5（s（n））＝2.

（c）若仅有3个非0比特间的距离是2n－2的整数倍，则有2个序列v（n），WH（v（n））＝5，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m＋x，亦或v（n）＝u（n），故有M5（s（n））＝3.

（d）若分别有2对非0比特之间的距离为2n－2的整数倍，则仅有1个序列v（n），WH（v（n））＝5，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m＋x，亦或v（n）＝u（n），故有M5（s（n））＝2.

（ⅱ）若4个非0比特属于同一个子序列.

（b）若其中3个非0比特之间的距离为2n－2的整数倍，或者分别有2对非0比特间的距离为2n－2的整数倍时，则只有1个序列v（n），WH（v（n））＝5，使得LC5（s（n））＝LC（p（n）＋u（n）＋v（n））＝2n－2－2m＋x，亦或v（n）＝u（n），故有M5（s（n））＝2.

（2）当LC（u（n）＋v（n））＞2n－2－2m＋x时，根据引理1，有LC5（s（n））＝LC（q（n）＋u（n）＋v（n））＞2n－2－2m＋x.然而LC5（s（n））＝LC（q（n）＋u（n）＋v（n））＝2n－2－2m＋x，故有M5（s（n））＝1.

综上所述，M5（s（n））＝1，2，3或2n－m－2.

证毕.

3 结语

基于Games-Chan算法，分析了2n－周期非平衡二元序列s（n）的5－错线性复杂度所对应的错误序列，给出了5－错线性复杂度不大于2n－3、等于2n－2－2m和2n－2－2m＋x时5－错误序列的个数M5（s（n）），并通过计算机编程给予验证.

［1］ BERLEKAMP S R.Algebraic Coding Theory［M］.New York：Mcgraw-Hill，1968.

［2］ DING Cun-sheng，XIAO Guo-zhen，SHAN Wei-juan.The Stability Theory of Stream Ciphers.LNCS 561［M］.Berlin：Springer-Verlag，1991：85－88.

［3］ STAMP M，MARTIN C F.An Algorithm for the k-Error Linear Complexity of Binary Sequences with Period 2n［J］.IEEE Transactions on Information Theory，1993，39（4）：1 398－1 401.

［4］ KUROSAWA K，SATO F，SAKATA T，et al.A Relationship Between Linear Complexity and k-Error Linear Complexity［J］.IEEE Transactions on Information Theory，2000，46（2）：694－698.

［5］ 谭 林，戚文峰.F2上2n－周期序列的k－错误序列［J］.电子与信息学报，2008，30（11）：2 592－2 595.

［6］ 周建钦.具有2n线性复杂度的2n－周期二元序列的3－错线性复杂度［J］.应用数学学报，2013，36（3）：399－413.

［7］ 李鹤龄，戚文峰.Fp上pn－周期序列的k－错误序列［J］.通信学报，2010，31（6）：19－24.

［8］ 周建钦，刘 军.2n－周期二元序列的3－错误序列分布［J］.电子与信息学报，2012，34（8）：1 923－1 927.

（责任编辑 向阳洁）

5-Error Sequences of 2n-Periodic Unbalanced Binary Sequences

ZHOU Jian-qin1，2，WANG Hong-cui1

（1.Telecommunication School，Hangzhou Dianzi University，Hangzhou 310018，China；2.Computer Science School，Anhui University of Technology，Ma’anshan 243032，Anhui China）

The linear complexity and k-error linear complexity have been used to measure the randomness and the stability of key stream sequences.Both of them are extremely important for studying key stream strength.An effective method to calculate k-error linear complexity is to study error sequences with minimal Hamming weight.On this basis，the counting functions on the 5-error sequences with 5-error linear complexity up to 2n－3or equal to 2n－2－2m，2n－2－2m＋xare derived，and are verified by computer program.

key stream sequence；k-error linear complexity；k-error sequence

TN918

A

10.3969／j.issn.1007－2985.2013.05.007

1007－2985（2013）05－0027－04

2013－03－29

安徽省自然科学基金资助项目（1208085MF106）

周建钦（1963－），男，山东巨野人，安徽工业大学计算机学院教授，硕士，主要从事通信、密码学与理论计算机科学研究.