A Telegraph Equation with Hysteresis*
XU Long-feng,XUE Liang,2
(1.School of Math.&Phys.,Anhui University of Technology,Maanshan 243002,Anhui China;2.Department of Basic Courses,Anhui Vocational and Technology College,Tongling 244000,Anhui China)
A Telegraph Equation with Hysteresis*
XU Long-feng1,XUE Liang1,2
(1.School of Math.&Phys.,Anhui University of Technology,Maanshan 243002,Anhui China;2.Department of Basic Courses,Anhui Vocational and Technology College,Tongling 244000,Anhui China)
This paper discusses a telegraph equation with hysteresis.First,the properties of Ishlinskiǐhysteresis operator are given.Secondly,the existence of a C1+α,αstrong solution is obtained to this equation.Key words:Ishlinskiǐhysteresis operator;telegraph equation;monotone operator;strong solution
1 Introduction
Hysteresis is a kind of objective existence natural phenomenon.Since 1920s,people have begun to study Hysteresis phenomenon,to put forward a lot of models of hysteresis operators,and to discuss developing equation with Hysteresis(see ref.[1-4]).Krejci Pavel studied the quasi-stationary telegraph equation in ferromagnetic media in ref.[4]:

where Fis Ishlinskiǐhysteresis operator.Using difference method with regard to variable xand peculiarity of periodic function,he proved that if g∈Cω([0,1]×[0,∞)),then there exists at least a function u∈([0,1]×[0,∞))satisfying eq.(1),(2)under week meaning when t≥ω.This paper is devoted to the study for the solution of initial-boundary value problem to eq.(1).The main result is as follows:
Theorem1 If g∈C0,1(Q)(Q=(0,1)×(0,T]),a∈([0,1]),then there exists at least a solution u∈W(0,T;L2(0,1))∩L∞(0,T;H2(0,1))to eq.(1),(2)and

Especially,if g∈Cα0,1+α0(),a∈C1+α0([0,1])(0<α0<1),then there exists a constant 0<α≤α0such that u∈C1+α,α(¯Q).
2 IshlinskiǐOperator
Let us consider a free cylinder of length 2h,for any h>0,in the interior of which we move a piston.Let v(t)denote the position of the piston on the axis of the movement at the instant t∈[0,T],and let lh(v)(t)=λ(t)denote the position of the center of the cylinder.If the function v(t)is continuous and piecewise monotone,then

It is easy to see thatλ(t)is also continuous and piecewise monotone.In addition,it is easy to prove(see ref.[2])that let v,w∈C0([0,T])be piecewise monotone,then for any t∈[0,T],we have
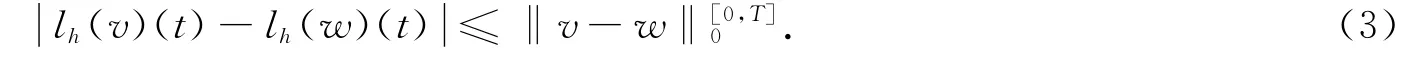
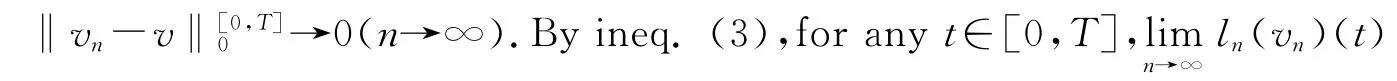
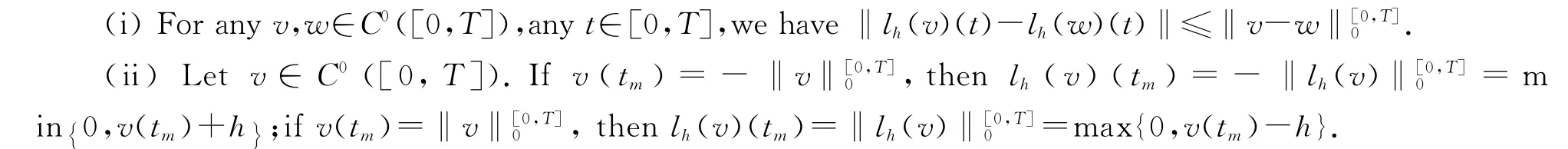
(iii)Let v∈C0([0,T]),0≤t0<t1≤T.If for any t∈[t0,t1],we have always v(t0)≤v(t)≤v(t1)(or v(t0)≥v(t)≥v(t1)),and there exists w∈C0[0,T]which is nondecreasing on[t0,t1](or nonincreasing)satisfying w(t0)=v(t0),w(t1)=v(t1),lh(w)(t0)=lh(v)(t0),then lh(w)(t1)=lh(v)(t1).
Take arbitraryφ[2]:(0,∞)→(0,∞)is a twice continuously differentiable function satisfying:(ⅰ)φ is increasing,φ(0+)=0,0<φ′(0+)<∞.There exists a>0,α∈(0,1),for any h>0,φ(h)<ahα.(ⅱ)For any r>0,denoteγ(r)=inf{-φ″(h),0<h≤r}.There exists b>0,β∈(0,α],r0>1such that for any r≥r0,γ(r)≥brβ-2.
It is easy to prove thatφis convex,φ′(h)≤φ(h)/h≤ahα-1,andφ′(h)≥b1hβ-1when h>r0,φ(h)≥b2hβwhen h>r1≥r0.Letψbe inverse function ofφ,denote s1=φ(r1),thenψ(s)≤C0s1/βwhen s>s1,and ψ′(s)≥C1s1/β-1,ψ″(s)≥C2(ψ(s))1+β-3α.For any v∈C0([0,∞))and any t∈[0,T],we define two operators Fand L:C0([0,T])→C0([0,T]),
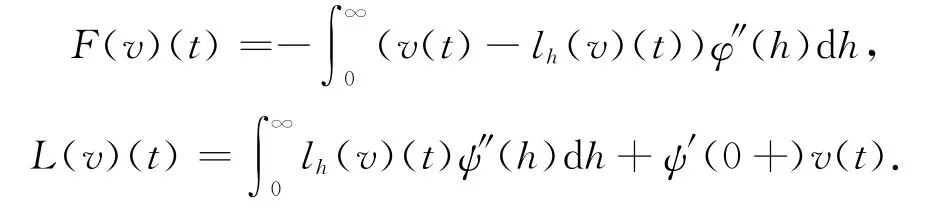
Lemma 1[2]Lis inverse operator of Fi.e.L=F-1,and for any v,w∈C0([0,T]),any t∈[0,T],it follows that

Corollary 1 For any v∈C0([0,T]),and any 0≤t1<t2≤T,we have
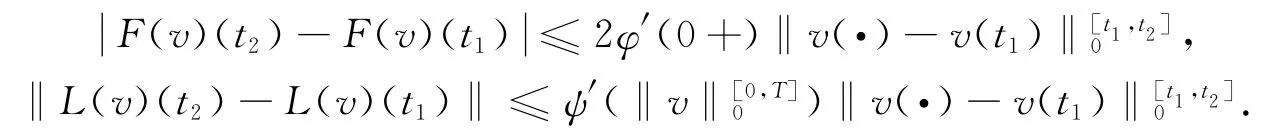
Lemma 2 Assume that v∈C0([0,T]),t0∈(0,T],ε>0,h1>h2>0.If vis nondecreasing in(t0-ε,t0]and lh1(v)(t0)=v(t0)-h1,then it follows surely that lh2(v)(t0)=v(t0)-h2;if vis nonincreasing in(t0-ε,t0]and lh1(v)(t0)=v(t0)+h1,then it follows surely that lh2(v)(t0)=v(t0)+h2.
Proof Let v be nondecreasing in(t0-ε,t0](method of proof is similar to that when vis nonin-creasing in(t0-ε,t0]).If there exists t*∈[0,t0]such thatby property(ii),lh(v)1(t*)=max{0,v(t*)-h1}.It is obvious that lh1(v)(t*)=v(t0)-h1as t*=t0,so lh2(v)(t*)=v(t0)-h2. When t*<t0,take t*<t1<t0such that v(t1)≤v(t)for any t∈[t*,t0].Noticing property(iii),we can assume that vis a segment of straight line on[t*,t1]and[t1,t0].Since lh1(v)(t0)=v(t0)-h1,it is easy to derive that lh1(v)(t*)=v(t*)-h1holds surely.lh1(v)(t1)=v(t1)+h1and v(t0)-v(t1)≥2h1;therefore,lh2(v)(t*)=v(t*)-h,lh2(v)(t1)=v(t1)+h2,lh2(v)(t0)=v(t0)-h2.
If there exists t*∈[0,t0]such that v(t*)=-‖v‖,then lh1(v)(t*)=min{0,v(t*)+h1}.Take t*<t2≤t0such that v(t2)≥v(t),for any t∈[t*,t0].If t2=t0,it is easy that lh1(v)(t*)=v(t*)+h1,lh1(v)(t0)=v(t0)-h1,so lh2(v)(t*)=v(t*)+h2,lh2(v)(t0)=v(t0)-h2.If t2<t0,take again t2<t1<t0such that v(t1)≤v(t)for any t∈[t2,t0].Since lh1(v)(t0)=v(t0)-h1,it is easy to derive that lh1(v)(t*)=v(t*)+h1,lh1(v)(t2)=v(t2)-h1,lh1(v)(t1)=v(t1)+h1and v(t0)-v(t1)≥2h1holds surely;therefore,lh2(v)(t*)=v(t*)+h2,lh2(v)(t2)=v(t2)-h2,lh2(v)(t1)=v(t1)+h2,lh2(v)(t0)=v(t0)-h2.
Now we introduce two operators Eand J:C0([0,T])→L∞(0,T).Take any v∈C0([0,T]),v(0)>0(or v(0)<0).If there exists aε>0such that vis nondecreasing(or nonincreasing)on[0,ε],then we set E(v)(0)=φ′(h0),J(v)(0)=ψ′(h0);otherwise,we set E(v)(0)=φ′(0+),J(v)(0)=ψ′(0+);if for any t0∈(0,T],there exists aε>0such that vis monotone in(t0-ε,t0],then we set E(v)(t0)=φ′(h0),J(v)(t0)=ψ′(h0);if how smallε>0is no matter,visn’t monotone in(t0-ε,t0],then we set E(v)(t0)=φ′(0+),J(v)(t0)=ψ′(0+).
Lemma 3 For any v∈C1([0,T]),we have F(v),L(v)∈O1([0,T])={φ∈C0([0,T]):φ′∈L∞(0,T)},and for any t0∈[0,T],F(v)′(t0)=E(v)(t0)v′(t0),L(v)′(t0)=J(v)(t0)v′(t0).
Proof We prove only the first formula.The second formula is similar to the first proof.
If v′(t0)=0,by lemma 1,it is easy to derive F(v)′(t0)=0=E(v)(t0)v′(t0);if v′(t0)=a>0(a<0is similar),and there exists aε>0such that vis strictly monotone increasing in(t0-ε,t0+ε)∩[0,T],then
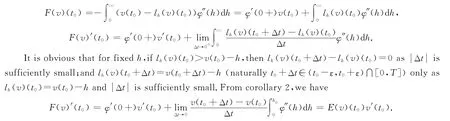
Corollary 2 For any v∈H1(0,T),we have that F(v),L(v)belong to H1(0,T)and DtF(v)(t)=E(v)(t)Dtv(t),DtL(v)(t)=J(v)(t)Dtv(t)a.e.[0,T].
Lemma 4 If vis a segment of straight line on[t0,t1],then(L(v)(t1)-L(v)(t0))·(v(t1)-v(t0))≥ψ′(0+)(v(t1)-v(t0))2.
3 Proof of Main Theorem

Lemma 5 Eq.(4),(5),(6)have at least solution v∈H1(0,T;L2(0,1))∩L∞(0,T;H),where H={φ∈H1(0,1):φx(0)=φx(1)=0}.

By definition of operator L,under the case that,...,are all known,(x)depends only on
By corollary 1and lemma 4,φnmis continuous and monotone with regard to(x).ObviouslyH→H*is strictly monotone,continuous and coercive,so it is also mapping fully,and there exists(x)as the solution of eq.(7).


By ineq.(11),(13),it yields

Let wm(x,t)be the function obtained by interpolating linearly value.For n=0,1,...,m,wm(x,nk)=(x)a.e.[0,1].In addition,for(n-1)k<t≤nk,n=1,...,m,denote(x,t)=(x)a.e.[0,1],so eq.(7)turn into

From ineq.(12),(14),we get

From ineq.(15),(17),we have
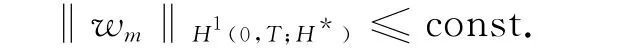
Therefore,there exist v,wsuch that(possibly taking subsequences):vm→vin H1(0,T;L2(0,1))week,and in L∞(0,T;H)week star;→vin Hγ(0,T;L2(0,1))week,for anyγ<,and in L∞(0,T;H)week star;wm→win H1(0,T;H*)week.
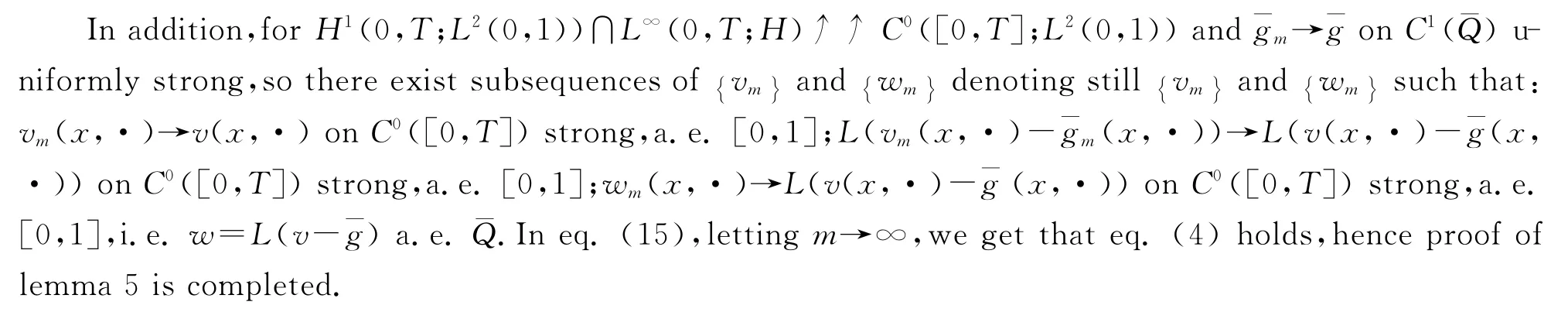

Reference:
[1] KRASNOSELSKII M A,POKROVSKII A V.Systems with Hysteresis[M].Moscow:Nauka,1983.
[2] PAVEL KREJCI.Hysteresis and Periodic Solutions of Semilinear and Quasilinear Wave Equations[J].Mathematische Zeitschrife,1986,193:247-264.
[3] PAVEL KREJCI.Periodic Solutions of a Parabolic Equation with Hysteresis[J].Mathematische Zeitschrife,1987,194:61-70.
[4] MAYERGOYZ I D.Mathematical Models of Hysteresis[M].New York:Springer-Verlag,1991.
[5] LADYZENSKAAJA O A.Linear and Quasi-Linear Equations of Parabolic Type[M].American:The American Mathematical Society,1968:204-210.
O175.29 Document code:A
10.3969/j.issn.1007-2985.2013.05.003
1007-2985(2013)05-0006-05
*Received date:2013-01-12
Supported by National Natural Science Foundation of China(11001001);Natural Science Foundation of Anhui Province Office of Education(KJ2010A043)
Biography:XU Long-feng(1952-),male,was born in Anqing City,professor of School of Math.&Phys.,Anhui U-niversity of Technology;research area is partial differential equations.

